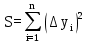Ммвпиэ лаб.работа 15. Отчет по лабораторной работе 15 Получение математической модели по результатам однофакторного пассивного эксперимента

• Название: Отчет по лабораторной работе 15 Получение математической модели по результатам однофакторного пассивного эксперимента
• Анкор: Ммвпиэ лаб.работа 15
• Дата: 05.11.2022
• Размер: 38.48 Kb.
• Имя файла: pi17.docx
• Тип: Отчет; #770682

Белорусский государственный университет информатики и радиоэлектроники


Отчет

по лабораторной работе №15

«Получение математической модели по результатам однофакторного пассивного эксперимента»

Выполнил:

студент ФТК

гр. 962101

Сорокин Е. В.
Проверил:

Журавлёв В. И.

Минск 2012

1. 
   Цель работы
   

Сгенерировать с помощью ЭВМ результаты опытов однофакторного пассивного эксперимента и, используя их, получить математическую модель объекта.

2. 
   Ход работы
   

Сгенерировали результаты однофакторного эксперимента

Таблица 1

№	x	y	№	x	y
1	176	5,2	19	135,4	9,4
2	173,7	5,4	20	133,1	9,5
3	171,5	5,7	21	130,9	9,9
4	170,4	5,8	22	129,7	10
5	169,2	5,9	23	128,6	10,1
6	168,1	6,1	24	127,5	10,2
7	164,7	6,3	25	124,1	10,5
8	163,6	6,5	26	123	10,7
9	162,5	6,8	27	178,2	10,9
10	161,3	7	28	180,5	11,2
11	159,1	7,3	29	183,9	11,5
12	155,7	7,6	30	186,1	11,8
13	153,4	8	31	190,7	12,2
14	150	8,4	32	194	12,6
15	145,5	8,6	33	196,3	12,8
16	143,3	9	34	199,7	13,2
17	139,9	9,2	35	201,9	13,4
18	137,6	9,3	36	203,1	13,5

На прямоугольную координатную сетку нанесли точки с координатами (x₁, y₁), … , (x_n, y_n) и по виду диаграммы разброса (корреляционного поля) параметров x и y выбрали три элементарные функции, с помощью которых можно описать зависимость между yи х: линейная, гипербола, степенная.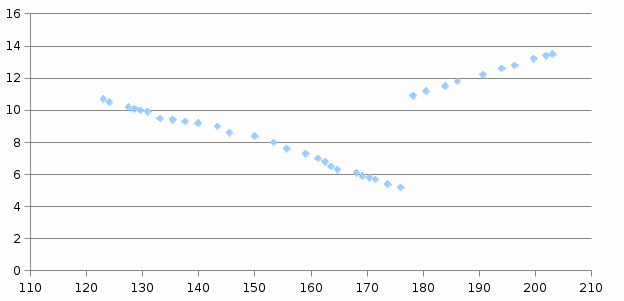



Рисунок 1 – Диаграмма разброса параметров х и у

Таблица 2

Модель	Коэффициент а		Коэффициент b			Критерий Фишера		Решение о пригодности модели	Относительная ошибка Δ, %
	значение	tрасч	значение	tрасч		Fрасч	Fкр
1.Линейная y=ax+b	0,028	1,661	4,642	1,670	204,6973486	2,759	4,11	непригодна	26,75
2.Показате-льная y=beax; lny=ax+ lnb	0,002	1,014	1,856	5,715	2,794	1,028	4,11	непригодна	11,85
3.Степенная y=bxa; lny=lnb+ alnx	0,220	0,688	1,066	0,658	2,839	0,473	4,11	непригодна	11,85

Гипотеза о наличии линейной регрессии между параметрами и откликом y отвергается: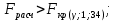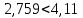





Оценка коэффициента a признается статически незначимой, а коэффициента b - значимой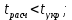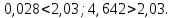





О качественности линейного уравнения регрессии можно судить также по значению коэффициента детерминации R²=0,075. Коэффициент детерминации R² показывает, какая доля вариации отклика y объясняется изменениями x. Чем ближе R² к единице, тем лучше функция y = φ(x) описывает поведение отклика y. Считают, что модель удовлетворительно описывает y, если R² ≥0,8. Проверка адекватности построенной регрессионной модели исходным данным является обязательной. Для адекватной модели обычно рассчитывается характеристика точности, например, средняя относительная ошибка: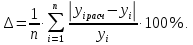



Считают, что модель хорошо описывает поведение y, если Δ ≤ 5%.
Исходные данные для второй модели:

Таблица 3

№	x	ln y	№	x	ln y
1	176	1,648659	19	135,4	2,24071
2	173,7	1,686399	20	133,1	2,251292
3	171,5	1,740466	21	130,9	2,292535
4	170,4	1,757858	22	129,7	2,302585
5	169,2	1,774952	23	128,6	2,312535
6	168,1	1,808289	24	127,5	2,322388
7	164,7	1,84055	25	124,1	2,351375
8	163,6	1,871802	26	123	2,370244
9	162,5	1,916923	27	178,2	2,388763
10	161,3	1,94591	28	180,5	2,415914
11	159,1	1,987874	29	183,9	2,442347
12	155,7	2,028148	30	186,1	2,4681
13	153,4	2,079442	31	190,7	2,501436
14	150	2,128232	32	194	2,533697
15	145,5	2,151762	33	196,3	2,549445
16	143,3	2,197225	34	199,7	2,580217
17	139,9	2,219203	35	201,9	2,595255
18	137,6	2,230014	36	203,1	2,60269

Гипотеза о наличии линейной регрессии между параметрами и откликом y не принимается, т.к.: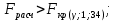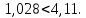





Оценка коэффициента a признается статически незначимой, а коэффициента b - значимой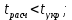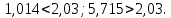




Значение коэффициента детерминации R²=0,029.
Исходные данные для третьей модели:

Таблица 4

№	ln x	ln y	№	ln x	ln y
1	5,170484	1,648659	19	4,908233	2,24071
2	5,15733	1,686399	20	4,891101	2,251292
3	5,144583	1,740466	21	4,874434	2,292535
4	5,138149	1,757858	22	4,865224	2,302585
5	5,131081	1,774952	23	4,856707	2,312535
6	5,124559	1,808289	24	4,848116	2,322388
7	5,104126	1,84055	25	4,821088	2,351375
8	5,097424	1,871802	26	4,812184	2,370244
9	5,090678	1,916923	27	5,182907	2,388763
10	5,083266	1,94591	28	5,195731	2,415914
11	5,069533	1,987874	29	5,214392	2,442347
12	5,047931	2,028148	30	5,226284	2,4681
13	5,033049	2,079442	31	5,250702	2,501436
14	5,010635	2,128232	32	5,267858	2,533697
15	4,980176	2,151762	33	5,279644	2,549445
16	4,96494	2,197225	34	5,296816	2,580217
17	4,940928	2,219203	35	5,307773	2,595255
18	4,924351	2,230014	36	5,313698	2,60269

Гипотеза о наличии линейной регрессии между параметрами и откликом y не принимается, т.к.: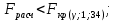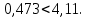





Оценка коэффициентов a и b признается незначимой, т.к. для значимости коэффициента должно выполняться условие: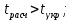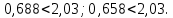




Значение коэффициента детерминации R²=0,014.
Вывод: в ходе работы было установлено, что ни одна из элементарных функций не подходит для адекватного описания представленных результатов опыта однофакторного пассивного эксперимента. По F-критерию пригодной не является ни одна модель, к тому же средняя относительная ошибка во всех случаях достаточно велика. А т.к. считают, что модель хорошо описывает поведение y, если Δ ≤ 5%, то все модели являются непригодными для описания экспериментальных данных.