ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2 Изучение основного закона динамики поступательного движения. Отчет по лабораторной работе 2 Изучение основного закона динамики поступательного движения
 Скачать 119.52 Kb. Скачать 119.52 Kb.
|
Филиал РТУ МИРЭА в г. Фрязино Кафедра общенаучных дисциплин ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №__2__ «Изучение основного закона динамики поступательного движения» по дисциплине «Физика» Выполнил студент группы ФКБ?-??-?? Аноним А.А. (учебная группа) Принял Кандидат физико-математических наук Белихов А.Б. Лабораторные работы выполнены «?» ?? 2022г. (подпись студента) «Зачтено» «??» ?? 2022г. (подпись руководителя) Фрязино 2022 ИЗУЧЕНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ Приборы и принадлежности: установка с блоком и грузами, секундомер, добавочные грузики. Теоретическое введение Первый закон динамики (закон инерции) отражает свойство материи быть в вечном движении: всякое тело сохраняет состояние прямолинейного равномерного движения (или покоя) до тех пор, пока воздействие со стороны других тел не заставит его изменить прежнее состояние. Тело массы м, движущееся по инерции равномерно и прямолинейно, обладает постоянной скоростью о (v << c) и, следовательно, неизменным импульсом (количеством движения) mv. Опыты показывают, что если на данное тело действует в течение некоторого времени ∆t другое тело, то при этом тело изменяет свою скорость и, следовательно, импульс. Это обстоятельство привело к образованию понятия силы (и импульса силы). Силой F называется мера действия, производимого со стороны другого тела на данное и заключающегося в изменении у данного тела скорости. Импульсом силы называется произведение силы на время ее действия (F∆t). Изучение внешних воздействий на данное тело позволило Ньютону сформулировать основной закон динамики поступательного движения: изменение импульса тела равно им пульсу силы и совершается вдоль прямой, по которой действует сила. Основной закон динамики можно записать следующим образом: F∆t=∆(mv). (1) При скоростях движения, значительно меньших скорости света, масса тела не зависит от скорости. Учитывая это обстоятельство, а также то, что величина 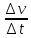 есть среднее ускорение а, характеризующее изменение скорости при внешнем воздействии, можно основной закон динамики поступательного движения записать: есть среднее ускорение а, характеризующее изменение скорости при внешнем воздействии, можно основной закон динамики поступательного движения записать:F=ma (2) Если на одно и то же тело массы м последовательно действует то сила F1, то сила F2, то ускорения а1 и а2 которые приобретает при этом тело, относятся друг к другу как действующие силы, то есть 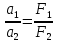 (3) (3)В случаях, когда на тело массы м. одновременно действует несколько сил, в уравнение (2) следует подставлять результирующую силу (то есть геометрическую сумму всех сил). Если результирующая сила действует на систему тел, перемещающихся с одним ускорением, то под массой m следует понимать сумму масс тел этой системы. В справедливости основного закона динамики (2) и его следствия (3) можно убедиться экспериментально. II. Описание аппаратуры и метода измерений. 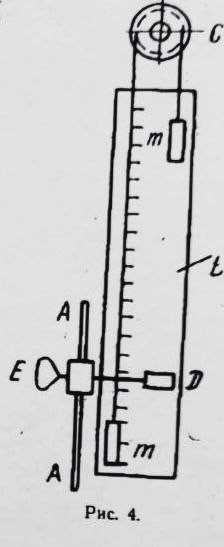 На стене монтирована длинная масштабная рейка в (рис. 4). У ее верхнего конца расположен легкий блок С, который вращается около горизонтальной оси с небольшим трением. Через блок перекинута нить с двумя одинаковыми цилиндрами. Каждый из них имеет массу м. На стене монтирована длинная масштабная рейка в (рис. 4). У ее верхнего конца расположен легкий блок С, который вращается около горизонтальной оси с небольшим трением. Через блок перекинута нить с двумя одинаковыми цилиндрами. Каждый из них имеет массу м.По металлическому прутку А может перемещаться плат форма D. Она закрепляется винтом Е в любом месте прутка. На описанной установке, аналогичной машине Атвуда, можно произвести изучение основного закона динамики поступательного движения. Рассмотрим систему двух равных цилиндров на нити, перекинутой через блок, в равновесии. Система, выведенная из равновесия легким толчком руки вскоре после толчка, останавливается. Замедленное движение системы обусловливается силой трения на осн блока. Сила трения может быть компенсирована грузиком массы µ. Такой грузик приложен к прибору. Рассматриваемую систему можно привести в равноускоренное движение следующим образом. На оба цилиндра наложим равные грузики (вес каждого из них Р2, масса m2). На правый цилиндр поместим еще два грузика: один из них компенсирует трение, второй (вес его Р1, масса m1) приводит систему в равноускоренное движение. Массу, равную (2m + 2m2 + m1 + µ) Равнодействующая сил, приложенных к системе, состоящей из цилиндров и грузов, равна Р1 и сообщает системе ускорение а1. Уравнение (2) применительно к ускоренному движению рассматриваемой системы тел принимает вид: P1=[2(m+m2) +m₁+µ)]*a₁. (4) Если грузик Р2 переложить левого цилиндра на правый, то общая масса системы останется неизменной. Величина же равнодействующей силы увеличится и будет равна (2P2 + Р1). В этом случае система получит ускорение а2. Основной закон динамики запишется: 2P2 +P1 = [2 (m + m2) + m1 + µ] 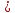 a2. (5) a2. (5)Деля (4) на (5) почленно, имеем 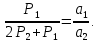 (6) (6)Соотношение (6) представляет собою следствие основного закона динамики применительно к системе тел, движущихся равноускорено под действием силы тяжести. Ускорения а1 и а2 в равноускоренном движении можно рассчитывать из выражений 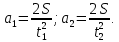 (7) (7)где S- пройденный путь, а 4 и 12 время, необходимое на прохождение этого пути под действием грузиков Р1 и 2P2+P1. Искомое отношение ускорений 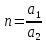 с учетом выражений (7) равно с учетом выражений (7) равно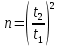 (8) (8)III. Порядок выполнения работы 1. Получают у лаборанта необходимые приборы. 2. Знакомятся с установкой, с методом перемещения платформы. 3. Платформу D (рис. 4) закрепляют в некотором положения. 4. Цилиндры нагружают грузиками Р2. На правый цилиндр, кроме того, помещают грузики Р1 и µ. 5. Определяют секундомером время t2 прохождения пути под действием грузика Р1. Для этого располагают нижний торец правого цилиндра в нужном положении и освобождая его, пускают в ход секундомер. В момент удара цилиндра о платформу секундомер останавливают. Записывают в таблицу результаты пяти измерений времени. 6. Перемещают грузик Р2 с левого цилиндра на правый. Определяют пятикратно время t2 прохождения того же пути под действием грузиков Р1+2Р2. Записывают результаты измерений t2 в таблицу. IV. Обработка результатов измерений По средним значениям времени рассчитывают по формуле (8) отношение ускорений п, а также абсолютную по грешность измерения: 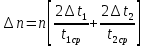 (9) (9)где ∆t1 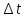 2 – случайные погрешности измерения времени. Они вычисляются методом Стьюдента и сравниваются с инструментальной погрешностью. 2 – случайные погрешности измерения времени. Они вычисляются методом Стьюдента и сравниваются с инструментальной погрешностью. Рассчитывают отношение n, результирующих сил, действующих на систему 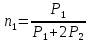 (10) (10)а также абсолютную погрешность 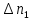 : :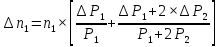 (11) (11)Сопоставляя n и n1, убеждаются, что равенство n=n1 не соблюдается; это обусловлено наличием погрешностей как при взвешивании грузов, так и при определении времени. Чтобы произвести оценку результата опыта, надо убедиться в том, что разность n н n1 по абсолютной величине не выходит за пределы погрешностей, допущенных при их определениях. Так как ∆(n-n1) < 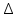 n+ n+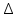 n1, то результат опыта будет удовлетворительным, если n1, то результат опыта будет удовлетворительным, если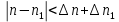 (12) (12)Практическая работа. Ход работы:
Рассчитаем по средним значениям времени отношение ускорений n: 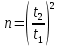 ; ; 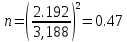 Также найдем абсолютную погрешность измерения: 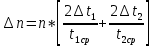 Расcчитаем ∆t по формуле Стьюдента: 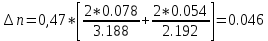 Рассчитаем отношение 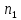 результирующих сил, действующих на систему: результирующих сил, действующих на систему: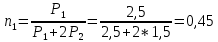 И также найдем абсолютную погрешность ∆ 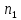 : :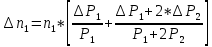 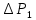 = =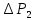 =0.05 =0.05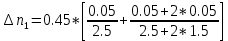 = 0.45[0.02 + 0.0272727273] = 0.12 = 0.45[0.02 + 0.0272727273] = 0.12Так как ∆(n- 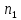 ) = ∆n+ ) = ∆n+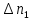 , результат опыта будет удовлетворительным, если , результат опыта будет удовлетворительным, если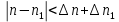 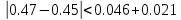 0.02 < 0.067 Выполняется. Вывод: в данной лабораторной работе был экспериментально доказан основной закон динамики поступательного движения Задача из задачника Чертова и Воробьёва Задача 2.1 Условие задачи: На гладком столе лежит брусок массой m=4 кг. К бруску привязан шнур, ко второму концу которого приложена сила F=10 Н, направленная параллельно поверхности стола. Найти ускорениеa бруска. Дано: Решение: m=4 кг 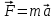 F= 10 Н 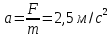  a - ? Ответ: 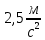 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



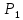 =2.5 г
=2.5 г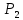 =5.5 г
=5.5 г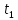
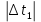
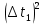
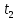
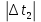
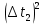
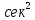
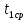 =3.634
=3.634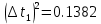
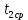 =2.363
=2.363