ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ И ТЕМПЕРАТУРНОГО КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ. отчет по мкт 2л. Отчет по лабораторной работе 2 определение удельного сопротивления и температурного коэффициента сопротивления проводников
 Скачать 306.18 Kb. Скачать 306.18 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Ивановский государственный химико-технологический университет» Кафедра технологии приборов и материалов электронной техники Отчет по лабораторной работе №2 ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ И ТЕМПЕРАТУРНОГО КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ Выполнили: студенты группы 2-9 Афонина К., Биточкин К. Проверил: Пивоваренок С.А. Иваново, 2021 Цель работы Изучить различные схемы триггеров в потенциальной системе элементов; овладеть методом логического проектирования структуры синхронного двухступенчатого триггера; получить навыки в сборке, наладке и экспериментальном исследовании заданного типа триггера. Цель работы Изучить различные схемы триггеров в потенциальной системе элементов; овладеть методом логического проектирования структуры синхронного двухступенчатого триггера; получить навыки в сборке, наладке и экспериментальном исследовании заданного типа триггера. Цель работы: исследование температурной зависимости сопротивления проводников, определение температурного коэффициента удельного сопротивления. Теоретическое введение Проводниками называются вещества, в которых в случае электростатического равновесия электрическое поле равно нулю, т. е. некомпенсированные заряды проводников локализуются в бесконечно тонком поверхностном слое, а если электрическое поле отлично от нуля, то в проводнике возникает электрический ток. Прохождение электрического тока в них обусловлено в подавляющем большинстве случаев движением электронов, поэтому металлы и сплавы относятся к проводникам с электронной проводимостью или проводникам первого рода. При приложении внешнего электрического поля напряженностью Е к металлу с концентрацией электронов проводимости n они приобретают направленную составляющую скорости (скорость дрейфа Vдр) и в проводнике протекает ток, плотность которого j = enVдр . (1) При не слишком высокой напряженности поля скорость дрейфа носителей прямо пропорциональна Е: Vдр = E, где коэффициент пропорциональности - подвижность электронов. При этом j = enE. Обозначив произведение en = , выражение (1) можно записать в виде закона Ома: j = E . (2) Величина называется удельной проводимостью, а обратная ей величина = 1/ - удельным сопротивлением проводника. Концентрация свободных электронов в металлах практически не зависит от температуры. В связи с этим значение удельной проводимости определяется, в основном, средней длиной свободного пробега электронов в конкретном металле, которая, в свою очередь, — рассеянием их на дефектах и тепловых колебаниях решетки. Например, для чистых металлов значения удельного сопротивления являются минимальными. И наоборот, наличие примесей и дефектов в решетке приводит к увеличению удельного сопротивления. В чистых металлах совершенной структуры единственной причиной рассеяния являются тепловые колебания частиц в узлах решетки (рассеяние на фононах). Составляющая сопротивления, обусловленная рассеянием на фононах (т), при температурах, превышающих характеристическую температуру Дебая Т > D, прямо пропорциональна Т: т = (1/) = С T (3) Эксперимент показывает, что такая линейная зависимость т(Т) справедлива с точностью не хуже 10% и до температур порядка (2/3)D. Значит, отмеченная линейная зависимость обычно выполняется при комнатной температуре и выше. Количественной характеристикой температурной зависимости удельного сопротивления проводников является температурный коэффициент удельного сопротивления , который численно равен относительному изменению удельного сопротивления при изменении температуры на один градус: = 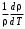 . (4) . (4)В общем случае зависит от температуры, но в относительно узком температурном интервале удельное сопротивление линейно изменяется с температурой: 2 = 1[1+(T2-T1)], (5) где 1 и - удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к началу температурного диапазона, то есть к температуре T1; 2 - удельное сопротивление при температуре T2. В практическом отношении важна температурная зависимость сопротивления проводника R(T), количественной характеристикой которой является R - температурный коэффициент сопротивления: 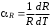 . (6) . (6)Изменение сопротивления с температурой может быть обусловлено как зависимостью (T), так и тепловым расширением материала. Тепловое расширение характеризуют температурным коэффициентом расширения материала l: 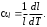 (7) (7)Легко показать, что = R + l . (8) Описание экспериментальной установки Схема экспериментальной установки показана на рис.1. Исследуемый проводник (1) помещен в термостат (2), температура в котором регулируется с помощью источника питания (3) и измеряется термометром (4). Длина и сечение проводника равны l=90м и S=0.05мм соответственно. Сопротивление проводника измеряется мультиметром (5). 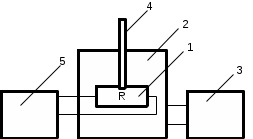 Рис.1. Блок-схема установки Процедура измерений. Подсоединить исследуемый проводник к входным клеммам прибора (5). Включив прибор в сеть, подготовить его к измерениям в соответствии с техническим описанием и инструкцией по эксплуатации. Измерить сопротивление проводника при комнатной температуре, занести полученное значение и температуру в лабораторный журнал. Включить блок питания термостата, и постепенно повышая мощность нагрева, измерить температурную зависимость сопротивления проводника до температуры 90oC. Данные занести в таблицу. Постепенно снижая температуру, выполнить аналогичные измерения при остывании проводника. Ход работы Построить температурную зависимость сопротивления. Обработать экспериментальные данные методом наименьших квадратов и определить температурный коэффициент сопротивления R . По зависимости R(T) найти сопротивление проводника при Т= 20 оС. Вычислить удельное сопротивление при Т= 20 оС и сравнить со справочным значением для данного материала (табл.1). Вычислить температурный коэффициент удельного сопротивления с учетом значения l, сравнить результат расчета со справочными данными. 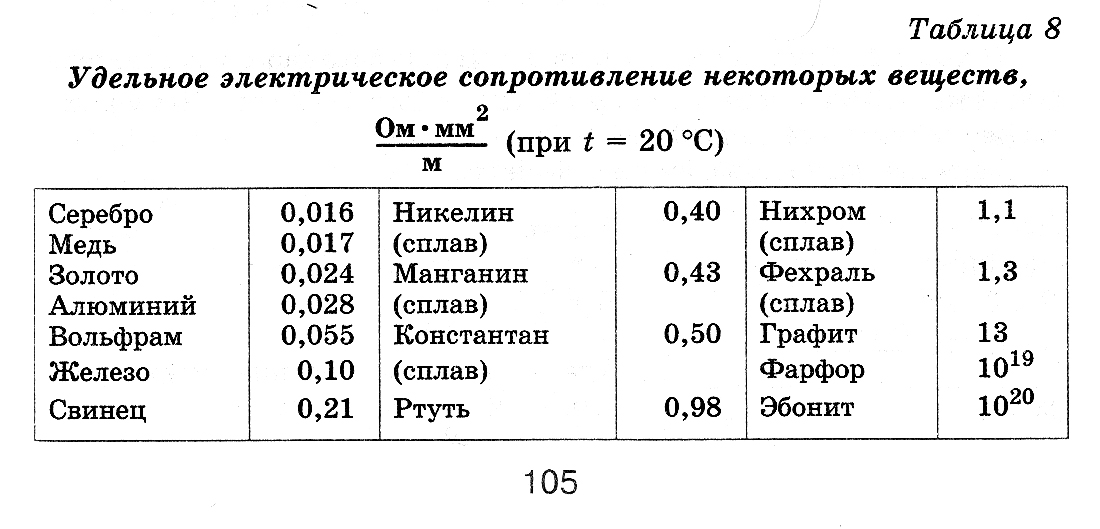 Табл.1 Измерения Таблицы зависимости сопротивления проводника от температуры при нагреве и охлаждении
Расчеты Обработав полученные данные методом наименьших квадратов, мы определили температурную зависимость сопротивления, которая выражается как R=0,0025T+0,7237 и построили её график (рис.2). На графике видно, что сопротивление проводника при T=20 оС составляет 0,768 кОм. Температурный коэффициент сопротивления R равен 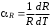 ; ; 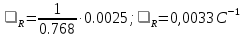 Удельное сопротивление проводника при Т= 20 оС 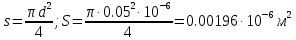 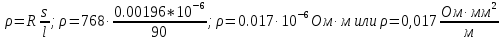 Сравнив полученное значение удельного сопротивления со справочными значениями, делаем вывод, что изучаемый проводник-медь. Температурный коэффициент удельного сопротивления Найдем по формуле(8). 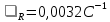 ; αl = 16,6 ∙ 10-6 K-1(из справочных данных) ; αl = 16,6 ∙ 10-6 K-1(из справочных данных) = 0,0032 +16,6 ∙ 10-6=0,0033166 K-1 Вывод: мы провели исследование температурной зависимости сопротивления проводников, нашли удельное сопротивление исследуемого проводника, определили его температурный коэффициент сопротивления и температурный коэффициент удельного сопротивления. Сравнили полученные значения с табличными данными и определили, что исследуемый проводник-медь. 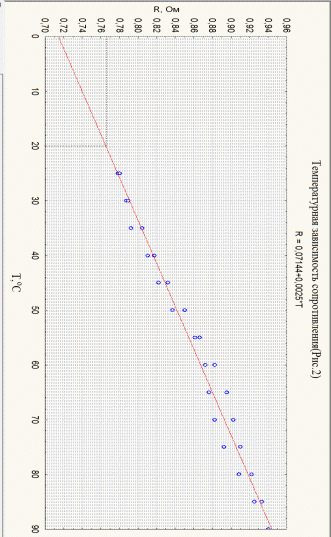 Вывод: мы провели исследование температурной зависимости сопротивления проводников, нашли удельное сопротивление исследуемого проводника, определили его температурный коэффициент сопротивления и температурный коэффициент удельного сопротивления. Сравнили полученные значения с табличными данными и определили, что исследуемый проводник-медь. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
