2Архитектура ВС. Отчет по лабораторной работе 2 по дисциплине Архитектура вычислительных систем
 Скачать 162.55 Kb. Скачать 162.55 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» (МАИ) Филиал «ВОСХОД» Кафедра Б21-ВСиТ «УТВЕРЖДАЮ» Преподаватель_____________ Яковлев В.С. «_____» _____________2022 г. ОТЧЕТ по лабораторной работе № 2 по дисциплине: Архитектура вычислительных систем на тему: «Конвейер» Вариант № 3Выполнил студент гр. ДВМ3-74_____________ Пралиев Н.Ж.«_____» _____________2022 г.Байконур 2022 г. Цель работы: изучение принципа конвейерной обработки информации. Постановка задачи Построить временную диаграмму выполнения программы при использовании конвейера и при его отсутствии в соответствии с вариантом задания. Исследовать наличие межкомандной зависимости на каждом уровне. Определить такт работы конвейера в соответствии с заданием. Выбор обосновать. Определить время выполнения программы. Задание по варианту Вариант 3. Сравнить временную диаграмму последовательного выполнения команд и синхронного 7-ступенчатого конвейера. Программа: УМН А1, А2 СЛ А2, А3 СЛ А3, А4 УП 6 (условие не выполняется) СЛ А6, А7 1 Теоретическая часть Синхронный конвейер Конвейер – специальное устройство, реализующее такой метод обработки команд внутри микропроцессора, при котором исполнение команды разбивается на несколько этапов. На стадии выполнения каждая машинная команда разбивается на более элементарные операции. Для выполнения каждого этапа операции имеется отдельный аппаратный блок. Эти блоки соединены в линию так, чтобы результат выполнения в данном блоке некоторого этапа передавался для реализации очередного этапа на следующий блок. Если для выполнения любого этапа операции выделено одно и тоже время tТ (такт конвейера), то такой конвейер называется синхронным. Рассмотрим рабочий цикл процессора (Пр). Выполнение любой операции Пр складывается из нескольких различных этапов, каждый из которых выполняется своим функциональным узлом. Рассмотрим пример: выполнение одноадресной машинной арифметической операции. Этапы рабочего цикла: - этап 1 - формирование адреса команды – t1. - этап 2 - чтение команды из оперативной памяти (ОП) – t2. - этап 3 -формирование адреса операнда – t3. - этап 4 - чтение операнда из памяти – t4. - этап 5 - выполнение арифметической операции – t5. Если длительность i-ого этапа равна ti и все этапы выполняются последовательно, то tпосл = t1+ t2+ t3+ t4+ t5 (1.1) Временная диаграмма работы одноадресной машины при последовательном выполнения представлена на рисунке 1.1. Принято, что t1 = t3< t2= t4< t5= tT 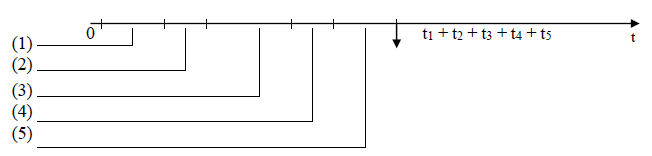 Рисунок 1.1 – Последовательная диаграмма работы машины Производительность определяется по формуле: 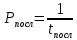 (1.2) (1.2)В данном примере все этапы выполняются разными функциональными узлами Пр, кроме 2 и 4, которые выполняются узлами оперативной памяти (ОП). Но ОП современных машин состоит из физических блоков с независимым обращением, т.е. тоже выполняются различными физическими устройствами. Далее поступим следующим образом: 1) Определяем такт конвейера. Обозначим через tТ (время такта) величину. tT = max{ti} (1.3) и будем требовать, чтобы для любых i=1,2,3, …, выполнялось условие ti + ti+1 > tT Иначе говоря, в качестве времени такта tТ выберем длительность наиболее продолжительного этапа операции, а саму разбивку на этапы производим таким образом, чтобы никакие два последовательных этапа не могли быть выполнены за время одного такта. Если при каком-либо разбиении операции на этапы последнее условие не выполняется для некоторого i, то два соседних этапа (i) и (i+1) объединим в один. 2) Другой способ, которым можно действовать в этом случае, состоит в том, чтобы разделить на части наиболее длительный этап и таким образом уменьшить время такта. Например, может оказаться, что самым длительным этапом является работа арифметического устройства, когда оно выполняет операцию умножения. Если это так, то множительное устройство можно построить в виде двух самостоятельных функциональных узлов, каждый со своими входными и выходными регистрами, из которых первый выполнял бы умножение множимого на младшие разряды множителя, а второй – умножение множимого на старшие разряды множителя и сложение с результатом, полученным первым функциональным узлом. Когда условия так или иначе, удовлетворены. Функциональные узлы, выполняющие последовательные этапы операции, целесообразно выстроить в единую конвейерную линию, в которой устройство, выполняющее этап 1, закончив его для одной операции, переходило бы в следующем такте к выполнению своего этапа для следующей операции и т.д. Временная диаграмма работы одноадресной машины при конвейерной работе представлена на рисунке 1.2. 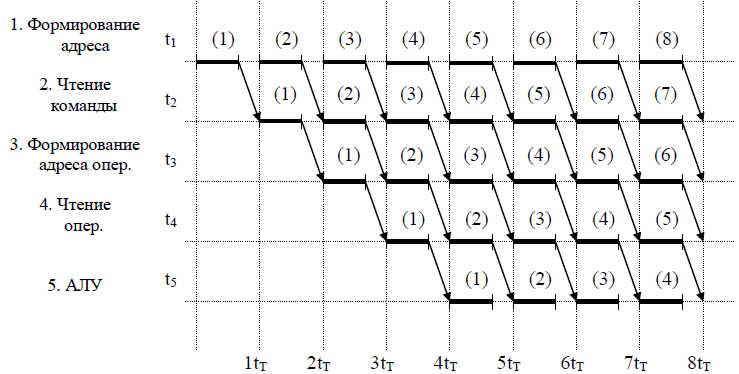 Рисунок 1.2 – Временная диаграмма при конвейерной работе Быстродействие в синхронном конвейере (номинальное) равно 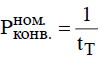 (1.5) (1.5)Количество этапов, на которые разделено выполнение каждой операции, называется глубиной перекрытия, т.е. определяет количество ступеней конвейера. В каждом такте на конвейере находится одновременно n последовательных операций. Чем больше глубина перекрытия, тем больший выигрыш в быстродействии может быть получен. Из условия ti ≤ tT, i = 1,2,…,n следует 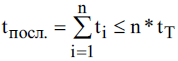 (1.6) (1.6)а из условий ti + ti+1 > tT следует 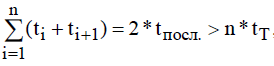 (1.7) (1.7)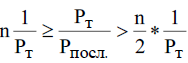 или 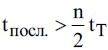 Таким образом, 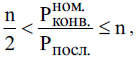 , (1.8) , (1.8)т.е. выигрыш в номинальном быстродействии получается в Отношение 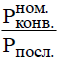 представляет собой предельный выигрыш в быстродействии машины при синхронном конвейере с глубиной перекрытия n. представляет собой предельный выигрыш в быстродействии машины при синхронном конвейере с глубиной перекрытия n. Реальный выигрыш по быстродействию оказывается всегда меньше предельного выигрыша. Это объясняется двумя факторами: 1) некоторые операции могут выполняться за меньшее количество тактов, чем обычные арифметические операции, в виду чего отдельные функциональные узлы, включенные в конвейер, при выполнении данных операций простаивают. 2) при выполнении некоторых операций на определенных этапах могут потребоваться результаты более поздних этапов предыдущих операций, либо при выполнении некоторых операций результаты определенных этапов могут влиять на более ранние этапы следующих, ввиду чего приходится приостанавливать конвейер. Этот фактор проявляется при выполнении операций условного перехода. Пример операции условного перехода по результату арифметической операции. Если бы временная диаграмма строилась по последовательному принципу, то такая операция выполнилась бы всего в 2 такта: формирование адреса, команда условного перехода и чтение команды условного перехода из ОП, после чего необходимо переходить к формированию адреса следующей команды. Однако при конвейерной организации условный переход оказывается длиннее обычных операций. Рассмотрим пример влияния на производительность конвейера команды условного перехода по результату арифметической операции при конвейерной обработке команд (рисунок 1.3). Временная диаграмма работы конвейера для следующих операций: (1) – арифметическая операция; (2) – пересылка данных в регистр; (3) – условный переход по результату арифметической операции; (4), (5), (6) – арифметические операции. 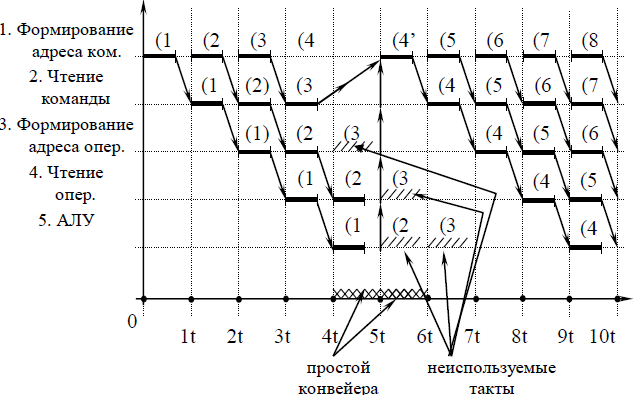 Рисунок 1.3 - Временная диаграмма работы конвейера Показан случай, когда условие передачи (УП) удовлетворяется, т.е. приходится заново формировать адрес следующей команды. Заштрихованы те такты, когда не используются отдельные устройства, включенные в конвейер. При выполнении операции (2) пересылка данных в регистр – в шестом такте простаивает АЛУ, а при выполнении (3) операции – УП – в пятом такте простаивает устройство формирования адреса операнда, в шестом – АЛУ. Простой конвейера равен двум тактам. После того, как из ОП прочитана команда УП (3), приходится ждать в течение одного такта – окончания арифметической операции (2), а затем тратить еще один такт – на формирование адреса следующей команды. При работе конвейера существует определенная зависимость между командами конвейера, которую необходимо учитывать при построении конвейера. 2 Практическая часть 2.1 Последовательное выполнение Пусть для выполнения заданных команд требуются следующие затраты времени: СЛ – 60 нс; УМН – 70 нс. Временная диаграмма последовательного выполнения команд представлена на рисунке 1.
Рисунок 1 – Временная диаграмма Последовательное выполнение команд займет 310 нс. Время на переход между тактами не учитывается. 2.2 Конвейерное выполнение Пусть выполнение команд осуществляется за 6 этапов со следующими затратами времени: Выборка команды (ВК). Чтение очередной команды из памяти и занесение ее в регистр команды – 10 нс; Декодирование команды (ДК). Определение кода операции и способов адресации операндов – 10 нс; Вычисление адресов операндов (ВА). Вычисление исполнительных адресов каждого из операндов в соответствии с указанным в команде способом их адресаций – 10 нс; Выборка операндов (ВО). Извлечение операндов из памяти. Эта операция не нужна для операндов, находящихся в регистрах – 10 нс; Исполнение команды (ИК). Извлечение операндов из памяти. Эта операция не нужна для операндов, находящихся в регистрах – 10 нс (для СЛ), 20 нс (для УМН); Запись результата (ЗР), Занесение результата в памяти – 10нс. Время на переход между тактами не учитывается. Временная диаграмма конвейера представлена на рисунке 2.
Рисунок 2 – Временная диаграмма конвейера Время выполнения команд на конвейере займет 110 нс. Расчет эффективности по сравнению с последовательным методом 310/110 = 2,8 Вывод В ходе выполнения лабораторной работы освоены навыки в построении конвейеров. Определена эффективность по сравнению с последовательным методом. |
