ЛБ2 отчёт. Отчет по лабораторной работе 2 по дисциплине
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Институт/Факультет - ИАМиТ наименование Кафедра теоретической механики и сопротивления материалов наименование кафедры РАСЧЁТ ПЛОСКОЙ ФЕРМЫ название работы Отчет по лабораторной работе № 2 по дисциплине СТРОИТЕЛЬНАЯ МЕХАНИКА наименование учебной дисциплины Выполнил Л.А. Овчарова Студент группы СМ-16-1 (подпись) И. О. Фамилия Проверил В.Б.Распопина К.т.н., доц. (подпись) И. О. Фамилия Иркутск – 2018 Цель работы: 1) формирование и статический расчёт плоской конечно-элементной модели ферменной конструкции; 2) анализ параметров напряжѐнно-деформированного состояния стержневой модели на основе полученных результатов; 3) оптимизация конструкции фермы. Исходные данные: плоская ферма, материал, предел текучести 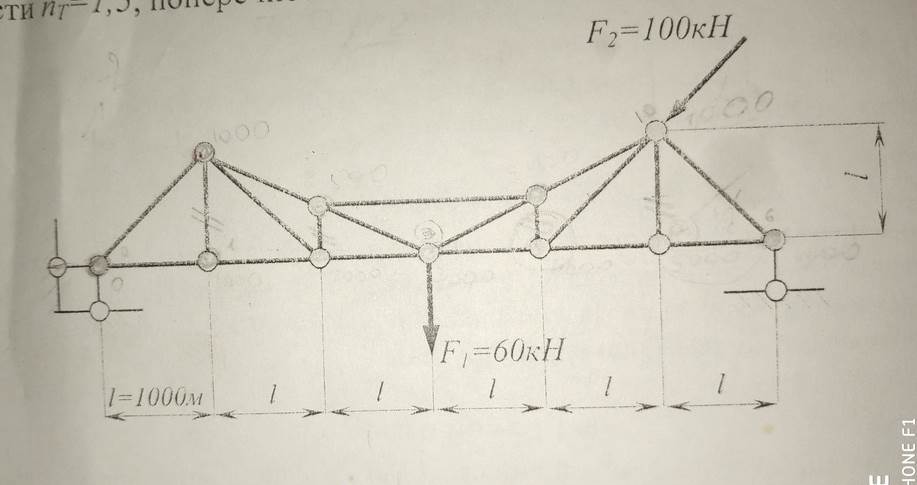 Рисунок 1. Исходный вид расчётной схемы плоской фермы Требуется: 1) сформировать расчётную модель заданной фермы в среде модуля APM Structure 3D; 2) выполнить статический расчёт заданной фермы; 3) определить значения реакций в опорах фермы с помощью средств модуля APM Structure 3D, сравнить полученные значения реакций со значениями, вычисленными в РГР «Расчёт плоской фермы на прочность»; 4) сформировать файл с исходными данными и с результатами вычислений в расширением rtf, ЛР2.rtf; 5)визуализировать в окне результатов эпюру продольной силы, сопоставить с данными файла ЛР2.rtf и с расчётами РГР «Расчёт плоской фермы на прочность» с последующим определением наиболее нагруженных и опасных стержней фермы; 6) визуализировать поля напряжений на объёмной модели фермы и сравнить полученную картину с расчётными значениями РГР «Расчёт плоской фермы на прочность» в таблице; 7) визуализировать карту нормальных напряжений для сечений наиболее опасных стержней фермы; 8) по результатам проектировочного расчёта, выполненного в РГР «Расчёт плоской фермы на прочность», оптимизировать модель заданной фермы; 9) выполнить статический расчёт оптимизированной фермы; 8) выполнить анализ оптимизированной фермы с помощью средств модуля APM Structure 3D; 9) внести изменение в оптимизированную модель фермы: изменить условие соединения стержней с шарнирного на жёсткое соединение; 10) выполнить статический расчёт изменённой модели фермы; 11) визуализировать в окне результатов эпюру продольной силы и определить наиболее нагруженные стержни фермы; 12) визуализировать поля напряжений на объёмной модели фермы; 13) визуализировать карту нормальных напряжений для наиболее опасных сечений стержней фермы; 14) выполнить сравнительный анализ двух моделей: определить какие виды нагружения испытывают стержни двух моделей фермы; сравнить эпюры продольных сил, значения и характер изменения нормальных напряжений. Анализ полученных результатов
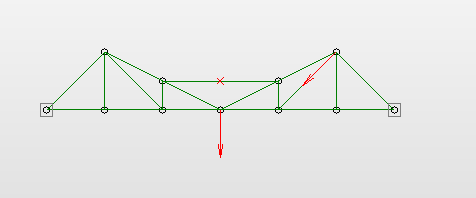 Рисунок 2. Модель фермы в среде модуля APM Structure 3D, представленная через продольные оси стержней фермы – окно «Вид спереди» 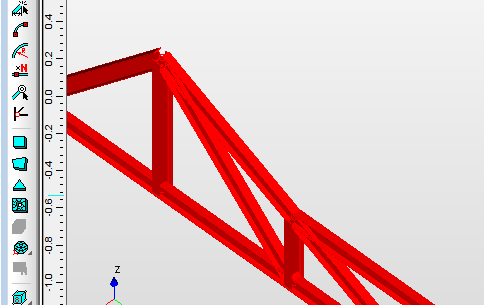 Рисунок 3. Модель фермы в среде модуля APM Structure 3D, представленная через объёмное изображение стержней фермы – окно «Произвольный вид»
Статический расчёт построенной модели заданной фермы выполнен. 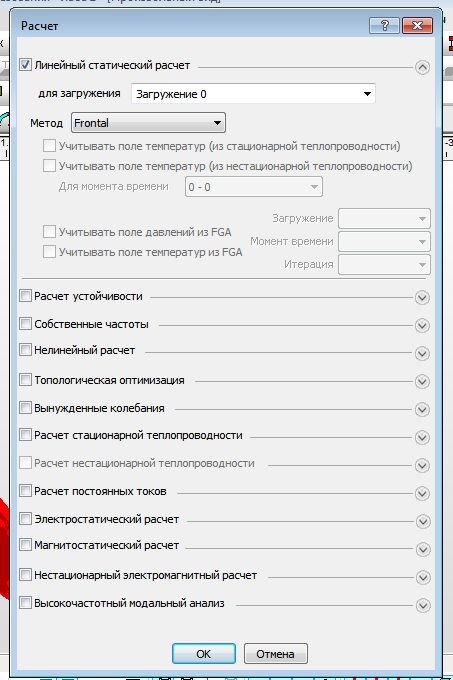 Рисунок 4. Диалоговое окно «Расчёт» - задание типа расчёта
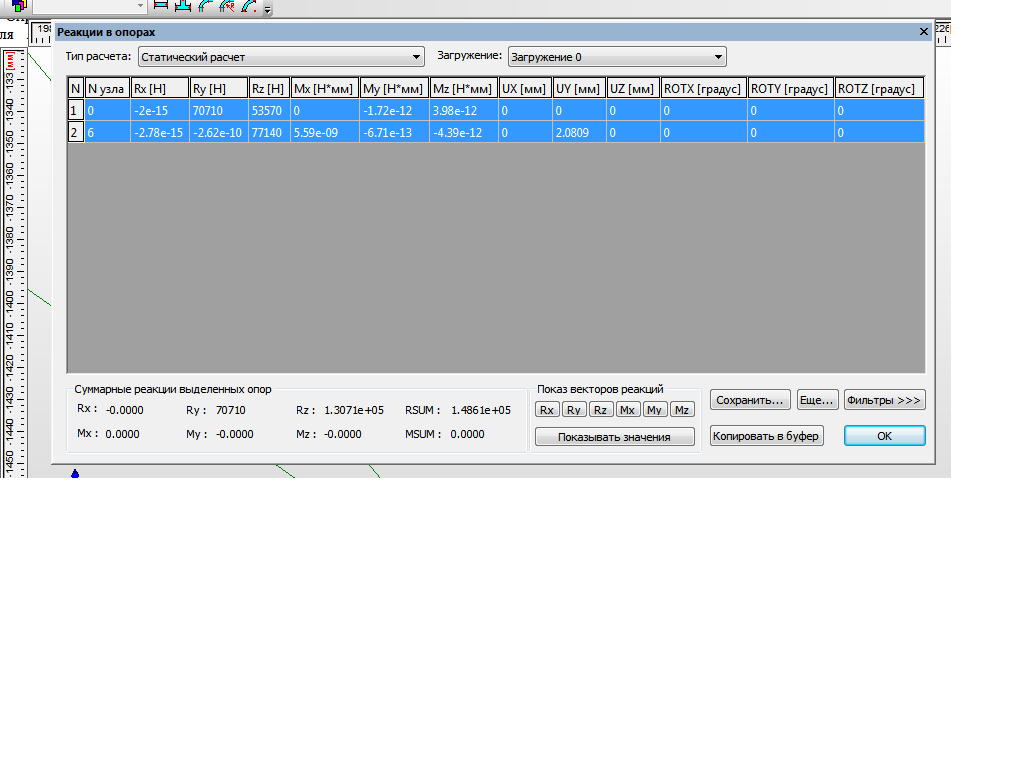 Рисунок 5. Диалоговое окно «Реакции в опорах» меню «Результаты» с результатами расчёта заданной фермы Таблица 1 Значения реакций, определённые в РГР и с помощью модуля APM Structure 3D
Направления реакций в опорах, определённые в РГР и в модуле APM Structure 3D, совпадают.
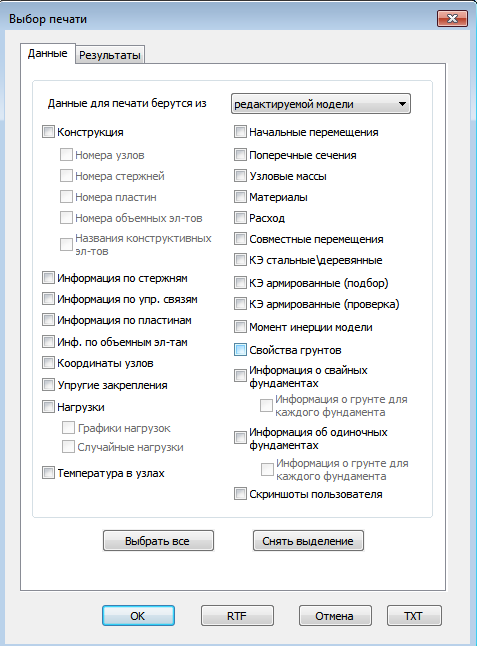 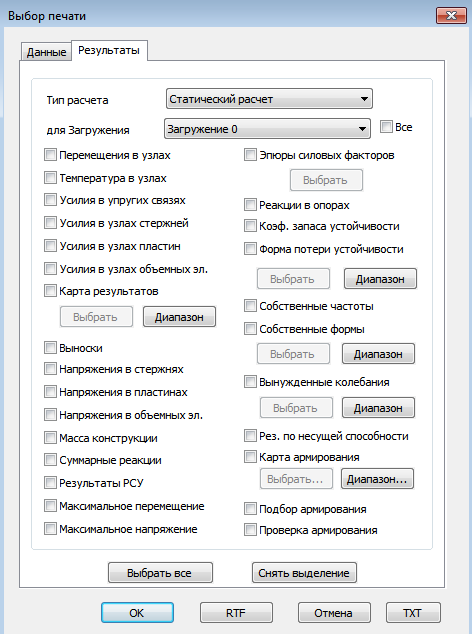 Рисунок 6. Диалоговое окно вывода данных о модели: а - данные модели на входе; б - данные модели по результатам расчёта
Окно результатов с эпюрой продольной силы представлено на рисунке 7. В таблице 2 приведены значения продольных сил, действующих в стержнях фермы, которые были определены в РГР и с помощью модуля APM Structure 3D из файла ЛР2.rtf в таблице «Усилия в узлах стержней». 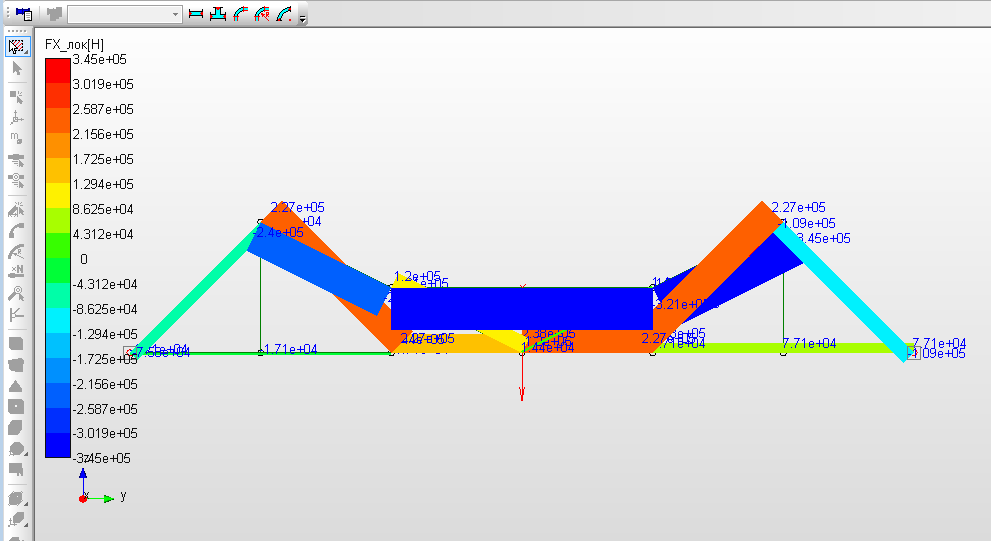 Рисунок 7. Эпюра продольной силы Таблица 2 Значения продольной силы, определённые в РГР и с помощью модуля APM Structure 3D
Качественный и количественный анализ значений продольных сил, действующих в стержнях фермы, позволил сделать вывод о наиболее нагруженных стержнях фермы. Такими стержнями в данном случае являются стержни с продольными силами N1-10=-239.572kH N1-5=227.278kH N5-10=-160.710kH N10-11=-321.420kH N2-11=-344.980kH N2-7=227.278kH N7-11=-160.710kH N7-6=237.850kH Значения продольных сил взяты из файла ЛР2.rtf. Отрицательный знак говорит о том, что стержень работает на сжатие, положительный знак говорит о растяжении стержня. Поскольку у всех стержней фермы поперечные сечения одинаковые и материал фермы пластичный, то можно однозначно определить наиболее опасные стержни фермы. То есть выбранные стержни являются таковыми. Ну а самым опасным является стержень, у которого продольная сила максимальна по модулю, то есть это стержень между узлами 2 и 11.
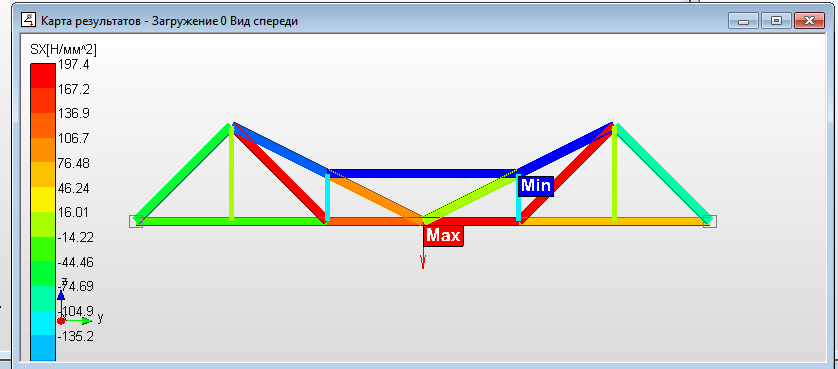 Рисунок 8. Поля нормальных напряжений на объёмной модели фермы Проведя соответствие между полученной шкалой численных значений напряжений и цветной шкалой, делаем вывод о том, что значительным растягивающим напряжения соответствует красный цвет, значительным сжимающим напряжениям соответствует синий цвет. Тогда согласно карте напряжений наиболее напряжёнными являются стержни фермы между узлами: 1-10, 10-11, 11-2 - окрашены синим цветом 1-5, 6-7, 7-2 - окрашены красным цветом Определим значения напряжений в этих стержнях. Воспользуемся функцией модуля APM Structure 3D - «Выноска». Результат представлен на рисунке 9.
Таблица 3 Значения нормальных напряжений, определённые в РГР и с помощью модуля APM Structure 3D
Если полагать, что наиболее точным будет результат, полученный с помощью модуля APM Structure 3D, тогда разницу в вычислениях можно оценить следующим образом: ∆1-10=(|σРГР1-10˗σAPM1-10 |)/(|σAPM1-10|)*100%=(|199.816-198.851 |)/ (198.851)*100%=0.485% ∆10-11=(|σРГР10-11˗σAPM10-11 |)/(|σAPM10-11|)*100%=(|267.85-266.782 |)/ (266.782)*100%=0.4% ∆11-2=(|σРГР11-2˗σAPM11-2 |)/(|σAPM11-2|)*100%=(|287.733-286.336 |)/ (286.336)*100%=0.488% ∆1-5=(|σРГР1-5˗σAPM1-5 |)/(|σAPM1-5|)*100%=(|189.505-188.642 |)/ (188.642)*100%=0.457% ∆6-7=(|σРГР6-7˗σAPM6-7 |)/(|σAPM6-7|)*100%=(|197.486-197.417 |)/ (197.417)*100%=0.035% ∆7-2=(|σРГР7-2˗σAPM7-2 |)/(|σAPM7-2|)*100%=(|189.505-188.642 |)/ (188.642)*100%=0.457% Поскольку разница результатов вычислений, полученных разными путями не превышает 2%, можно утверждать, что результаты вычислений нормальных напряжений, полученные двумя способами достоверны.
 Рисунок 10. Поле нормальных напряжений для поперечного сечения опасного стержня фермы
Таблица 4 Номера двутавров исходных и подобранных для наиболее напряжённых стержней
Сопоставим значения нормальных напряжений для исходных и новых стержней, рассчитанных в РГР и в среде модуля APM Structure 3D, таблице 5. Таблица 5 Значения нормальных напряжений, определённые в РГР и с помощью модуля APM Structure 3D, для исходных и новых стержней
В ходе проектировочного расчёта был изменён один параметр проектирования конструкции у наиболее напряжённых стержней. Этим параметром является площадь поперечного сечения данных стержней. Результатом изменения стало понижение опасных значений поля напряжений до приемлемого уровня в соответствии с характеристиками материала.
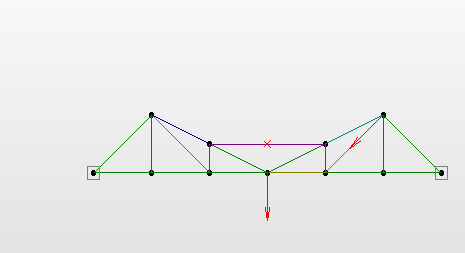 Рисунок 12. Геометрия модели после замены шарниров между стержнями фермы жёстким закреплением
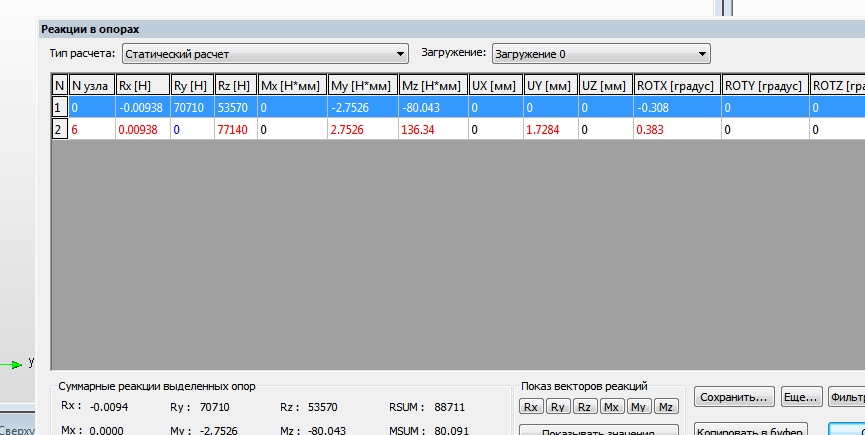 Рисунок 13. Результаты расчёта фермы с жёстко соединёнными стержнями в виде реакций в опорах Значения реакций в опорах, действующие в рабочей плоскости задачи не изменились. Их величина не зависит от структуры фермы и от способа соединения внутренних элементов фермы при условии, что выполняются условия геометрической неизменяемости системы. Ненулевые значения моментов и реакции по направлению, перпендикулярной плоскости задачи, а опорных узлах обусловлены тем, что вновь полученная модель закрепления формально является пространственной. Эти составляющие реакций можно обнулить путём изменения условий закрепления: заменить цилиндрический шарнир шаровым шарниром (рис. 14). После таких изменений по результатам статического расчёта получили значения реакций такие же, как в случае фермы с шарнирным соединением стержней (см. рис. 5). 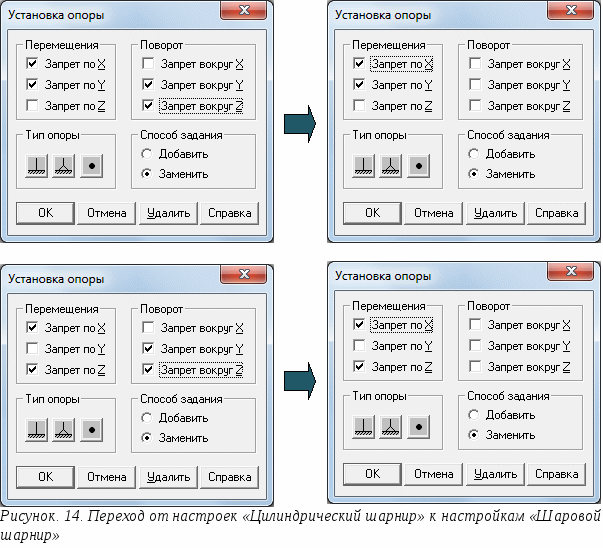
а) 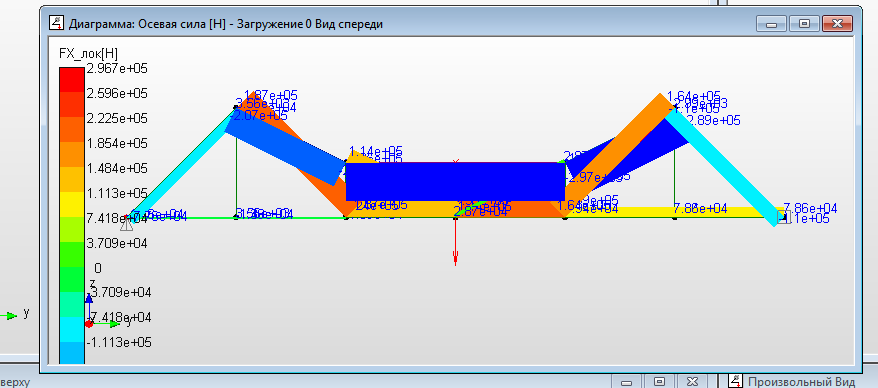 б) б)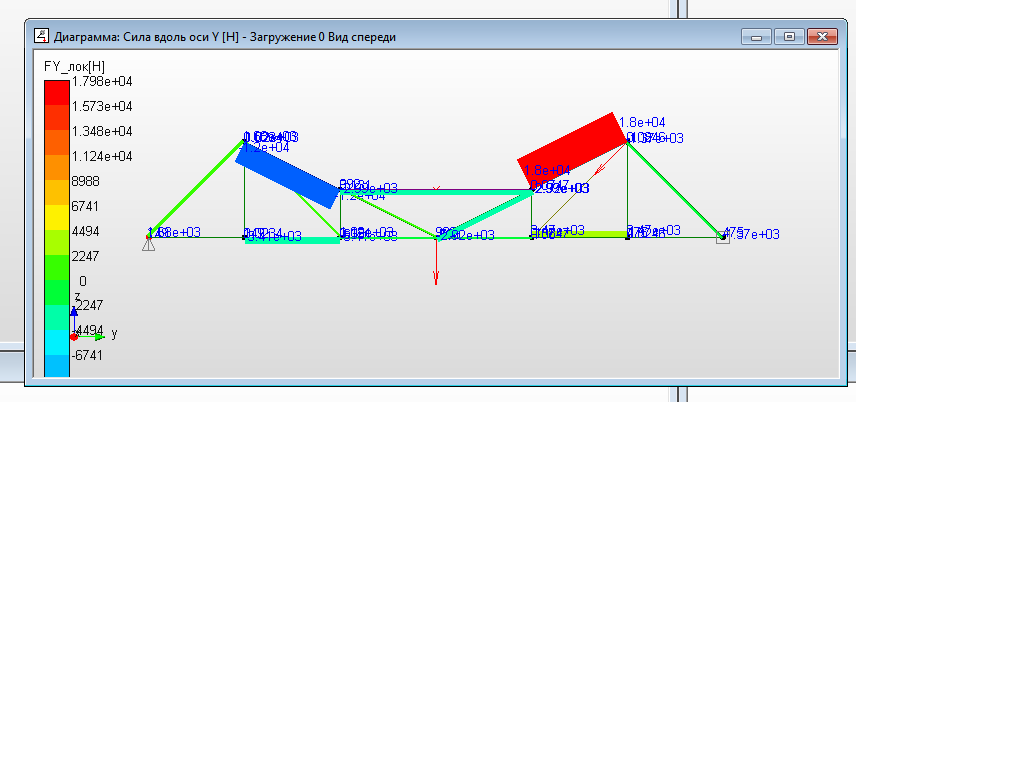 в) 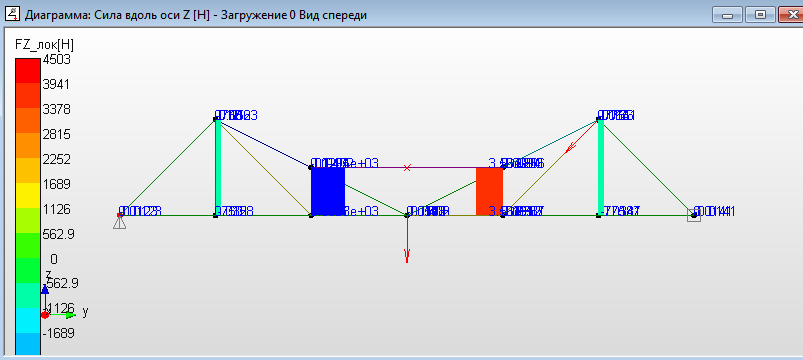 Рисунок 16. Диаграммы сил стержней - эпюры внутренних силовых факторов, действующих в поперечных сечениях стержней фермы: а - «Осевая сила» - продольная сила; б – «Сила вдоль оси Y» - поперечная сила, действующая в локальной плоскости стержня YX; в – «Сила вдоль оси Z» - поперечная сила, действующая в локальной плоскости стержня ZX а) 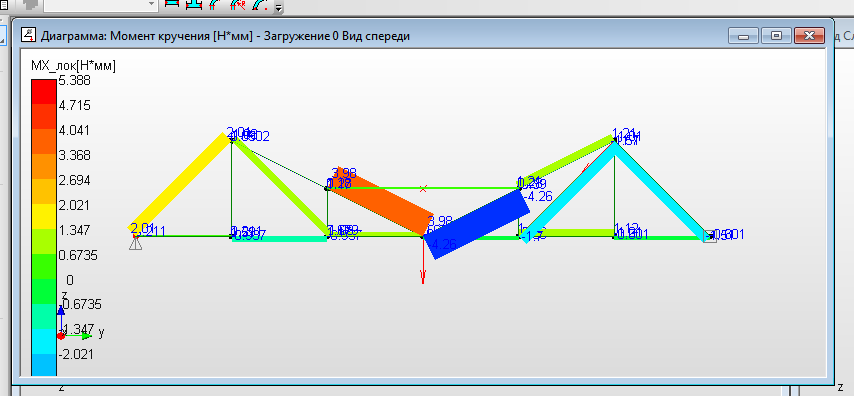 б) 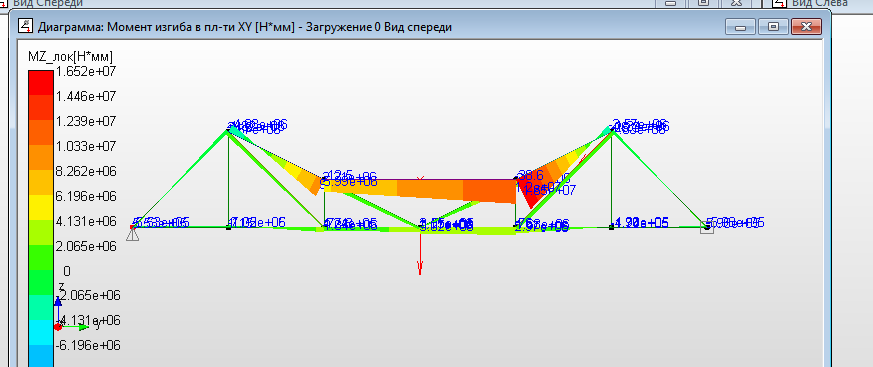 в) 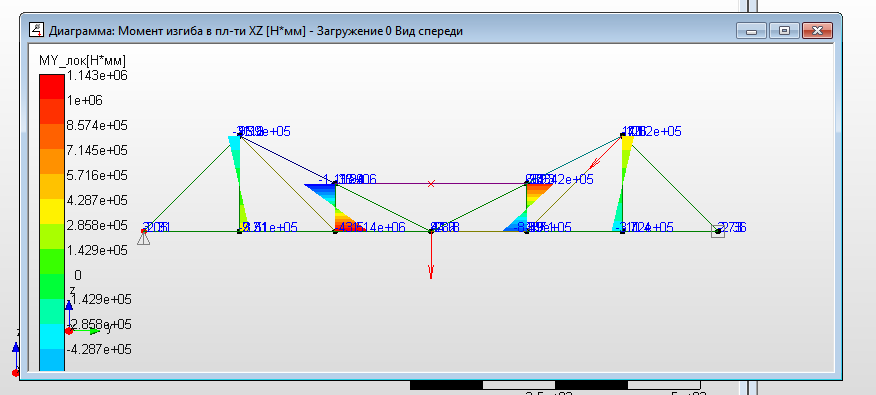 Рисунок 17. Диаграммы моментов в стержнях - эпюры внутренних силовых факторов, действующих в поперечных сечениях стержней фермы: а - «Момент кручения» - крутящий момент; б – «Момент изгиба в плоскости XY» - изгибающий момент, действующий в локальной плоскости стержня YX; в – «Момент изгиба в плоскости XZ» - изгибающий момент, действующий в локальной плоскости стержня ZX Общая картина показывает, что ферма испытывает общий пространственный вид нагружения, поскольку присутствуют все шесть внутренних силовых факторов для фермы в общем. Для каждого стержня картина не такая однозначная. Чтобы её уточнить следует, используя инструмент динамического ориентирования, проанализировать подробно для рассматриваемого стержня все шесть эпюр. Можно воспользоваться данными файла с расширением «rtf».
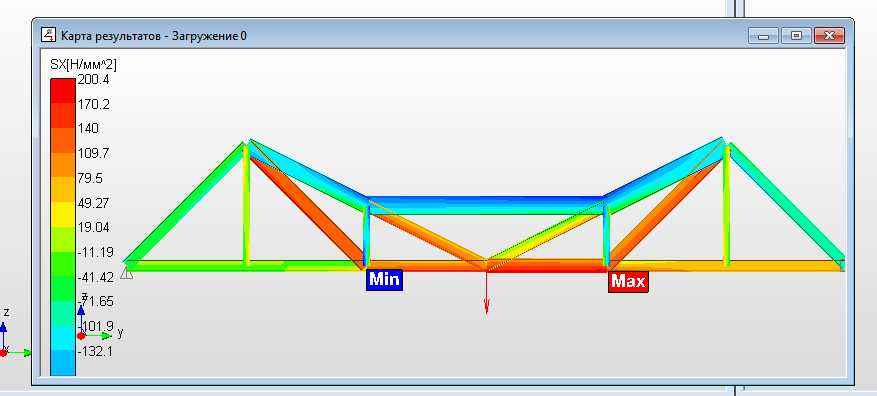 Рисунок 18. Поля нормальных напряжений на объёмной модели фермы
Анализируя поля напряжений на объёмной модели, выбрали наиболее нагруженные стержни. Затем, чтобы уточнить картину трансформировали объёмный вид в стержневой и для опасных стержней сделали выноски
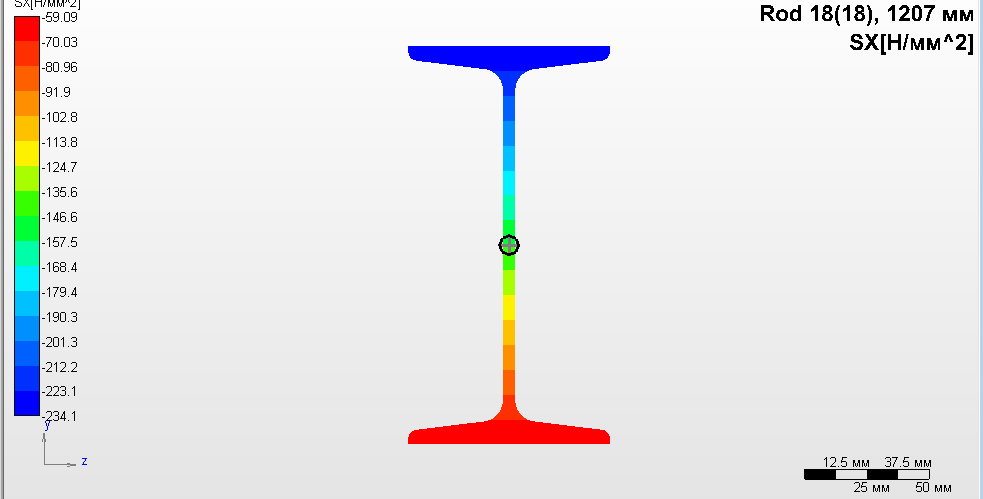 Рисунок 20. Поле нормальных напряжений для опасного поперечного сечения наиболее нагруженного стержня Характер распределения нормальных напряжений по рассматриваемому сечению свидетельствует о том, стержень испытывает внецентренное сжатие, поскольку нормальные напряжения все отрицательные и изменяются по высоте сечения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
