Энтропия сложной системы. Условная энтропия. Лабораторная2_Отчет. Отчет по лабораторной работе 2 Тема Энтропия сложной системы. Условная энтропия Преподаватель Курашкин С. О

• Название: Отчет по лабораторной работе 2 Тема Энтропия сложной системы. Условная энтропия Преподаватель Курашкин С. О
• Анкор: Энтропия сложной системы. Условная энтропия
• Дата: 24.05.2023
• Размер: 96.44 Kb.
• Имя файла: Лабораторная2_Отчет.docx
• Тип: Отчет; #1157303
• страница: 1 из 9

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»

Институт информатики и телекоммуникаций
Кафедра информационно-управляющих систем
Отчет по лабораторной работе №2

Тема: Энтропия сложной системы. Условная энтропия

Преподаватель _________Курашкин С.О.
Обучающийся БИЭ21-01 211211015 __________Навицкая А.А.

Красноярск 2023


Цель работы:

Закрепить теоретические знания и получить практические навыки при вычислении энтропии.

Задание:

Влияние помех в канале связи описывается канальной матрицей, с помощью условных вероятностей P(Y/X) и P(Х/Y), где X – источник информации, Y – приемник информации.

1. Провести исследование канала информации со стороны источника информации и со стороны приемника информации.

По результатам исследования определить:

- Потери информации Н(Y/x_i), которые приходятся на каждый переданный х_i сигнал и потери Н(Y/X) при передаче всех сигналов х;

- Потери информации Н(Х/у_j), которые приходятся на каждый принятый у_j сигнал и потери Н(Х/Y) при приеме всех сигналов y_j.

Исходные данные:

Р(у_j /x_i) и Р(x_i / у_j) получить из матрицы совместных вероятностей, размером 10 × 10, которую задать самостоятельно.

2. Определить энтропию Н(Х,Y) двухбуквенного сочетания и условную энтропию Н(Y/X) заданного текстового сообщения.

Х – 32-х буквенный алфавит

Y – 32-х буквенный алфавит

Задание 1

Таблица совместных вероятностей:

xi/yi	y1	y2	y3	y4	y5	y6	y7	y8	y9	y10	pi p(xi)
x1	0,001	0,031	0,001	0,001	0,002	0,001	0,02	0,007	0,007	0,001	0,072
x2	0,004	0,01	0,02	0,01	0,001	0,003	0,012	0,003	0,017	0,005	0,085
x3	0,001	0,003	0,014	0,002	0,011	0,003	0,004	0,004	0,004	0,04	0,086
x4	0,002	0,03	0,005	0,002	0,001	0,007	0,013	0,018	0,005	0,017	0,1
x5	0,008	0,005	0,003	0,001	0,001	0,002	0,03	0,015	0,002	0,001	0,068
x6	0,001	0,002	0,007	0,003	0,003	0,01	0,01	0,02	0,003	0,007	0,066
x7	0,006	0,009	0,012	0,001	0,004	0,018	0,01	0,008	0,003	0,004	0,075
x8	0,001	0,001	0,05	0,04	0,015	0,06	0,012	0,006	0,01	0,05	0,245
x9	0,01	0,01	0,001	0,004	0,001	0,007	0,014	0,017	0,032	0,003	0,099
x10	0,015	0,02	0,014	0,02	0,006	0,011	0,001	0,003	0,01	0,004	0,104
ri p(yj)	0,049	0,121	0,127	0,084	0,045	0,122	0,126	0,101	0,093	0,132	1

Таблица условных вероятностей p (x_i / y_j)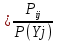

Канальная матрица от приемника Y к источнику X.

xi/yi	y1	y2	y3	y4	y5	y6	y7	y8	y9	y10
x1	0,0204	0,2562	0,0079	0,0119	0,0444	0,0082	0,1587	0,0693	0,0753	0,0076
x2	0,0816	0,0826	0,1575	0,1190	0,0222	0,0246	0,0952	0,0297	0,1828	0,0379
x3	0,0204	0,0248	0,1102	0,0238	0,2444	0,0246	0,0317	0,0396	0,0430	0,3030
x4	0,0408	0,2479	0,0394	0,0238	0,0222	0,0574	0,1032	0,1782	0,0538	0,1288
x5	0,1633	0,0413	0,0236	0,0119	0,0222	0,0164	0,2381	0,1485	0,0215	0,0076
x6	0,0204	0,0165	0,0551	0,0357	0,0667	0,0820	0,0794	0,1980	0,0323	0,0530
x7	0,1224	0,0744	0,0945	0,0119	0,0889	0,1475	0,0794	0,0792	0,0323	0,0303
x8	0,0204	0,0083	0,3937	0,4762	0,3333	0,4918	0,0952	0,0594	0,1075	0,3788
x9	0,2041	0,0826	0,0079	0,0476	0,0222	0,0574	0,1111	0,1683	0,3441	0,0227
x10	0,3061	0,1653	0,1102	0,2381	0,1333	0,0902	0,0079	0,0297	0,1075	0,0303

Таблица условных вероятностей p (y_j / x_i)