Отчет по лабораторной работе 3 Спектральный анализ случайных процессов по дисциплине
 Скачать 479.3 Kb. Скачать 479.3 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Томский политехнический Университет»  Инженерная школа ядерных технологий Направление 01.04.02 «Прикладная математика и информатика» ОТЧЕТ По лабораторной работе 3 Спектральный анализ случайных процессов по дисциплине: Цифровая обработка сигналов
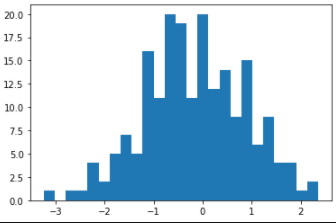
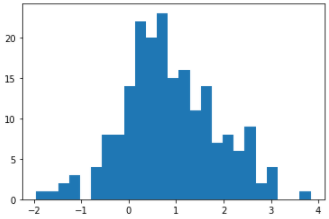
Томск – 2021 Оглавление ЗаданиеСгенерировать две последовательности x(n) и y(n) в виде выборки случайных данных с нормальным законом распределения с помощью датчика случайных чисел (ДСЧ). Значения математического ожидания и дисперсии выбрать из таблицы 1 в соответствии с вашим вариантом. Объем каждой выборки 200 значений. По выборкам получить оценки математического ожидания и дисперсии и сравнить с заданными. По каждой выборке построить автокорреляционные функции Rx(t) и Ry(t) соответственно. Объяснить, что они показывают и вычислить по ним оценки радиуса корреляции и дисперсии. Сравнить полученную оценку дисперсии с заданной. Путем ДПФ построить спектральные плотности по двум корреляционным функциям и объяснить, что они показывают. Оценить энергию сигнала(дисперсию) по спектральной плотности. Построить функцию взаимной корреляции Rxy(t), определить положение ее максимума и объяснить, что показывает это положение. Путем ДПФ построить взаимную спектральную плотность от взаимной корреляционной функции, разложить ее на взаимный амплитудный и фазовый спектры и объяснить, что они показывают. Провести анализ полученных результатов и написать отчет о проделанной работе. Цель работыПриобретение необходимых навыков по корреляционному анализу случайных процессов. Теоретическая частьАвтокорреляционная функция – выражает зависимость взаимосвязи между сигналом и его копией от значения сдвига копии по аргументу. Для детерминированного непрерывного сигнала 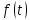 АКФ представляет собой интеграл: АКФ представляет собой интеграл: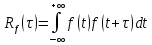 (1) (1)При представлении сигнала в виде вектора в функциональном пространстве, АФК – скалярное произведение вектора 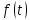 и и 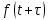 : :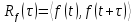 (2) (2)Для периодических сигналов, например sin или cos АФК рассчитывается за один период. При помощи АФК можно исследовать сигнал на присутствие в нем скрытых периодических составляющих. Функция взаимной корреляции - выражает зависимость взаимосвязи между двумя сигналами от значения сдвига одного сигнала относительно другого по аргументу:  (3) (3)Если сигналы представлены в виде дискретной выборки, то корреляционная функция выражается последовательностью 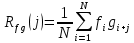 (4) (4)Радиус корреляции – значение 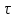 на котором значения процесса можно считать некоррелированными: на котором значения процесса можно считать некоррелированными: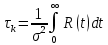 . (5) . (5) Любая функция может быть представлена в функциональном пространстве через ортогональный базис. Так как функции sin и cos, а также их гармоники ортогональны, через их систему можно представить любую функцию. Верно и обратное, зная коэффициенты и функции составляющие ортогональный базис можно восстановить любую функцию. Разложение периодической функции на сумму тригонометрических функций называется разложение Фурье: 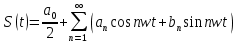 (6) (6)По формуле Эйлера выражение 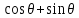 можно выразить через комплексное выражение можно выразить через комплексное выражение 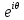 , где , где 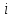 -мнимая единица. Тогда разложение Фурье принимает вид: -мнимая единица. Тогда разложение Фурье принимает вид: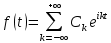 (7) (7)Дискретное преобразование Фурье – один из видов разложения функции в ряд Фурье. Сигнал представлен в виде цифровой последовательности размером N с интервалом дискретизации 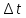 и длительностью и длительностью 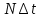 : :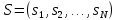 (8) (8)Длительность сигнала 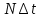 принимаем его периодом. Тогда S – вектор в N-мерном функциональном пространстве. Его можно выразить через N – мерный ортонормированный базис функций принимаем его периодом. Тогда S – вектор в N-мерном функциональном пространстве. Его можно выразить через N – мерный ортонормированный базис функций 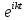 , где , где 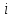 -мнимая единица, k = (0,1,2, …, N - 1). Комплексные коэффициенты Фурье определяются как скалярное произведение сигнала S на соответствующую базисную функцию: -мнимая единица, k = (0,1,2, …, N - 1). Комплексные коэффициенты Фурье определяются как скалярное произведение сигнала S на соответствующую базисную функцию: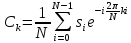 (9) (9)Энергия сигнала по теореме Парсеваля: 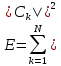 (10) (10) Фазой частотной составляющей является аргумент комплексного коэффициента Фурье. Основная частьНа языке Python генерируем последовательности случайных величин с нормальным распределением 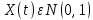 и и 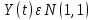 в количестве 200 значений в каждой с помощью генератора случайных чисел с равномерным распределением на интервале [0,1]. Результат представлен на Рис.1. в количестве 200 значений в каждой с помощью генератора случайных чисел с равномерным распределением на интервале [0,1]. Результат представлен на Рис.1.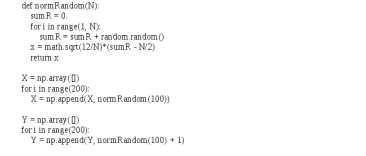
Рис. 1. Гистограммы случайных последовательностей X и Y Оценка среднего и дисперсии для выборок: 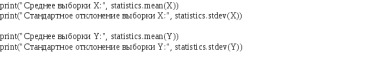 Среднее выборки X: -0.1625659738371587 Стандартное отклонение выборки X: 1.0415953865688774 Среднее выборки Y: 0.8707756490414005 Стандартное отклонение выборки Y: 0.9885475325426426 Рис. 2.Оценка среднего и дисперсии для выборок X и Y По формуле (4) вычисляем автокорреляционные функции для последовательностей X и Y и их функцию взаимной корреляции (Рис.3).  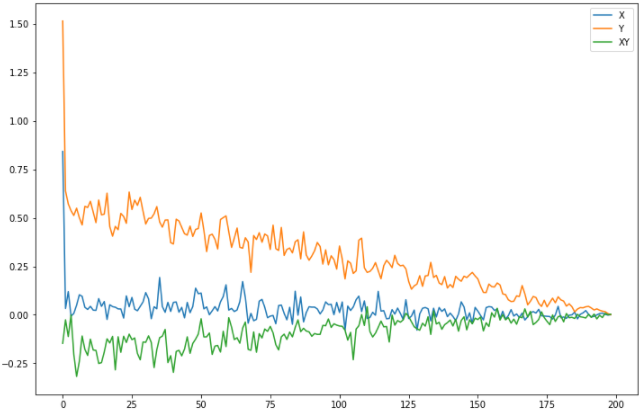 Рис. 3. Функции автокорреляций и взаимной корреляции последовательностей X и Y Так как последовательности конечные, при сдвиге наблюдается краевой эффект, когда количество парных произведений уменьшается. В этом случае предполагается, что за пределами последовательностей сигнал нулевой. Либо можно увеличить одну последовательность в два раза, обеспечив при этом адекватное сопряжение двух частей (Рис 4).  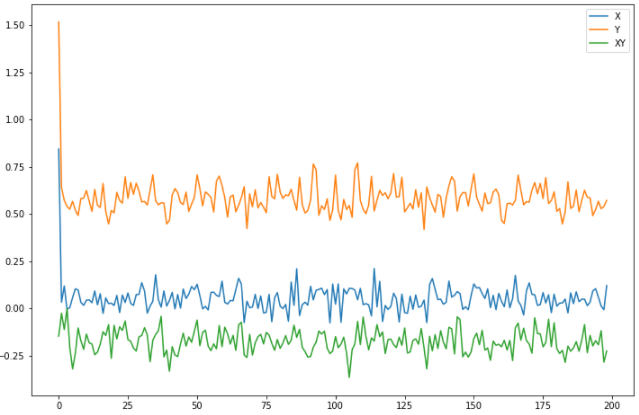 Рис. 4. Функции автокорреляций и взаимной корреляции последовательностей X и Y без краевых эффектов Так как сигнал Y не центрированный, то есть в нем присутствует постоянная составляющая, то для сравнения автокорреляционных функций сигналов и определения радиуса корреляции и дисперсии необходимо из функции автокорреляции вычесть квадрат постоянной составляющей (Рис.5).  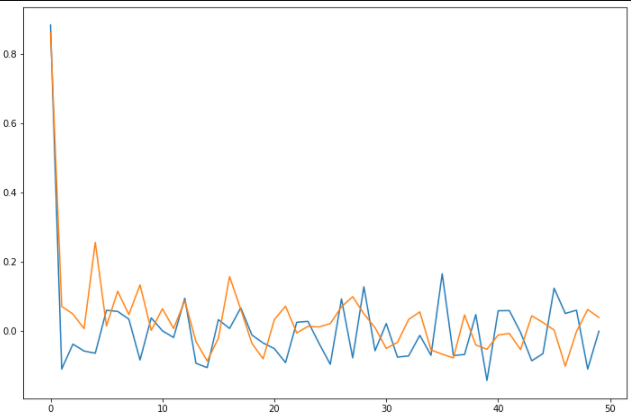 Рис. 5. Центрированные функции автокорреляции По Рис. 5 можно оценить дисперсии сигналов X и Y. Дисперсия равна значению центрированной функции автокорреляции в точке 0 (Рис. 6). D(X) = 0.8833304666848637 D(Y) = 0.8617546258778195 Рис. 6. Оценка дисперсии сигналов X и Y Радиус корреляции определяем по формуле (5). Так как процесс центрированный, интеграл равен нулю. Дисперсии сигналов равны значениям их функций автокорреляций в точке 0. Получаем: 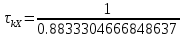 =1.1320791455920192 =1.1320791455920192 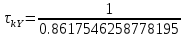 =1.1604231297062757 =1.1604231297062757 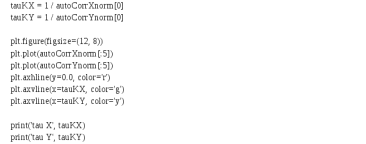 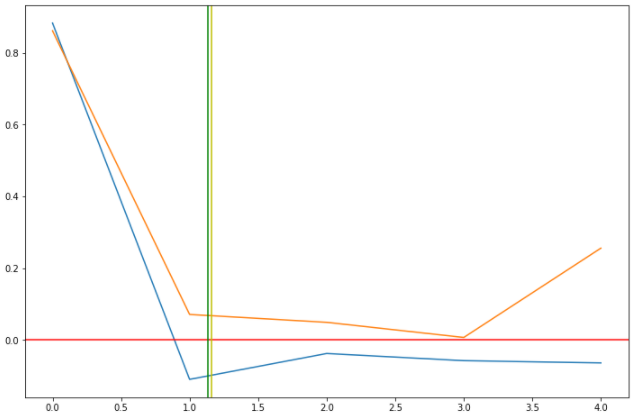 Рис. 7.Оценка радиусов корреляции сигналов X и Y На Рис.7 приведены оценки радиусов корреляции сигналов X (зеленая линия) и Y (желтая линия). На Рис. 8 приведен местоположение максимума функции взаимной корреляции сигналов X и Y. Так как максимум функции имеет отрицательное значение, то в этой точке сигналы X и Y имеют минимальное сходство. 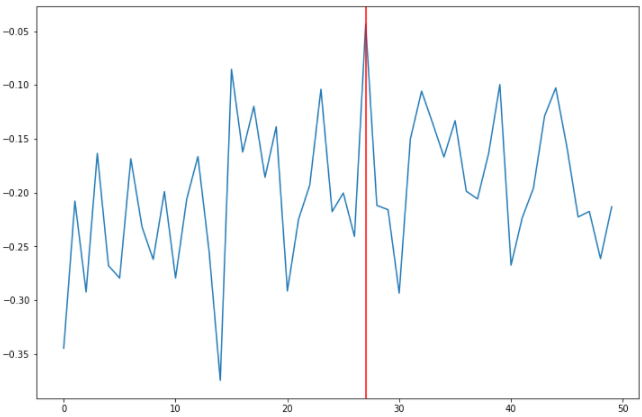 Рис. 8.Максимум функции взаимной корреляции При помощи дискретного преобразования Фурье строим спектральные плотности автокорреляционных функций сигналов X и Y (Рис. 9, Рис. 10)  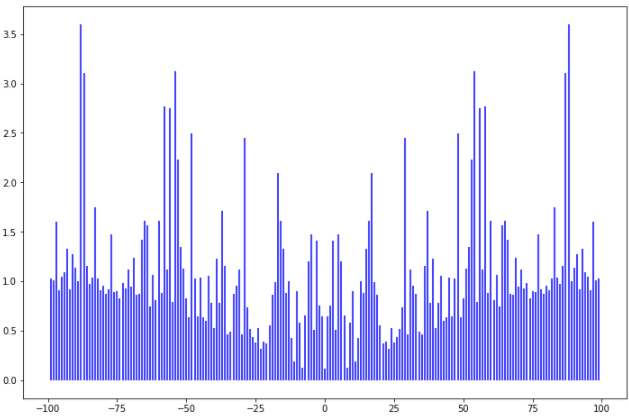 Рис. 9.Спектральная плотность автокорреляционной функции сигнала X 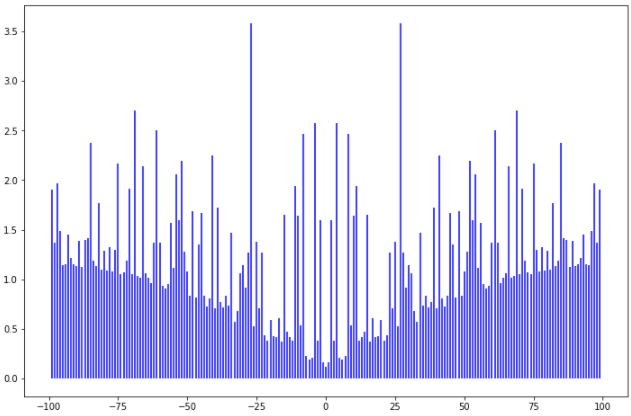 Рис. 10. Спектральная плотность автокорреляционной функции сигнала Y Каждая линия на графиках Рис 9, Рис 10 представляет составляющую частоту, присутствующую в сигнале, высота линии – амплитуду соответствующей частотной составляющей. Энергия сигнала по (10): 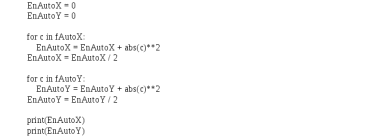 Энергия автокорреляции X: 158.64839015981255 Энергия автокорреляции Y: 182.24450407102864 При помощи дискретного преобразования Фурье строим частотный и фазовый спектр функции взаимной корреляции сигналов X и Y (Рис. 11, Рис. 12) 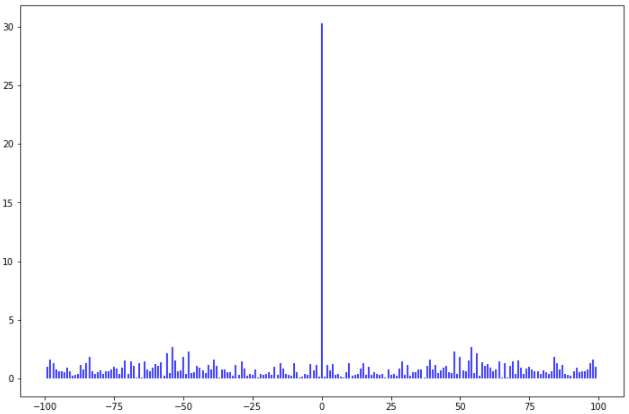 Рис. 11. Спектральная плотность функции взаимной корреляции сигналов X и Y 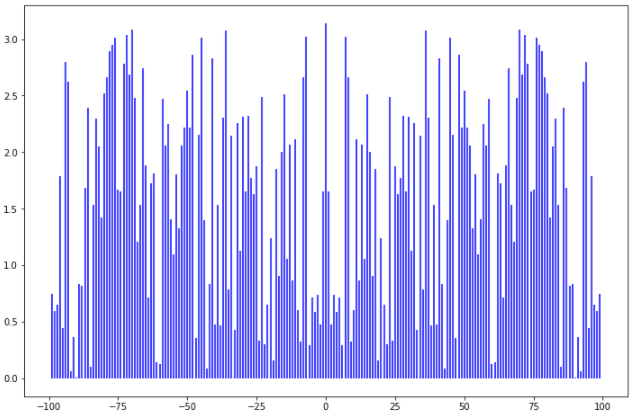 Рис. 12. Фазовый спектр функции взаимной корреляции сигналов X и Y Каждая линия на графике Рис 11 представляет составляющую частоту, присутствующую в сигнале, высота линии – амплитуду соответствующей частотной составляющей. Видно, что преобладает постоянная составляющая (f = 0). Каждая линия на графике Рис 12 представляет фазовый сдвиг соответствующей частотной составляющей, присутствующей в сигнале, высота линии – значение сдвига в радианах. ЗаключениеВ работе проведено исследование автокорреляционных функций сигналов и функции их взаимной корреляции. При помощи дискретного преобразования Фурье построены частотные и фазовые спектры сигналов. Приведены теоретические сведения, программный код, рисунки с результатами работы. Работа выполнена на языке Python в среде Jupyter Lab. ПриложениеКодзадания import random import math import numpy as np import matplotlib.pyplot as plt import scipy import statistics from scipy.stats import normaltest def normRandom(N): sumR = 0. for i in range(1, N): sumR = sumR + random.random() x = math.sqrt(12/N)*(sumR - N/2) return x X = np.array([]) for i in range(200): X = np.append(X, normRandom(100)) print(X) Y = np.array([]) for i in range(200): Y = np.append(Y, normRandom(100) + 1) print(X) n, bins, patches = plt.hist(X, bins = 25) plt.show() print(n) print(bins) Yn, Ybins, Ypatches = plt.hist(Y, bins = 25) plt.show() print(Yn) print(Ybins) print("Среднее выборки X:", statistics.mean(X)) print("Стандартное отклонение выборки X:", statistics.stdev(X)) print("Среднее выборки Y:", statistics.mean(Y)) print("Стандартное отклонение выборки Y:", statistics.stdev(Y)) k2, p = normaltest(X) alpha = 5e-2 print("p = {:g}".format(p)) if p < alpha: print("Нулевая гипотеза отвергается") else: print("Нулевая гипотеза не может быть отвергнута") def kf(S1, S2): print(len(S1), len(S2) ) n = len(S1) KF = [] for j in range(n-1): _sum = 0. for i in range(n-1): k = i+j if(k >= len(S2)): break _sum = _sum + S1[i]*S2[k] # load sum KF.append(_sum / n) return KF YL = np.append(Y, Y) XL = np.append(X, X) autoCorrX = kf(X, XL) autoCorrY = kf(Y, YL) CorrXY = kf(X, YL) CorrYX = kf(Y, X) plt.figure(figsize=(12, 8)) plt.plot(autoCorrX) plt.plot(autoCorrY) plt.plot(CorrXY) plt.legend(['X', 'Y', 'XY']) autoCorrXnorm = (autoCorrX - (statistics.mean(X))**2) # / autoCorrX[0] autoCorrYnorm = (autoCorrY - (statistics.mean(Y))**2) #/ autoCorrY[0] plt.figure(figsize=(12, 8)) plt.plot(autoCorrXnorm[:50]) plt.plot(autoCorrYnorm[:50]) #plt.plot(CorrXY) print("D(X) = ", autoCorrXnorm[0]) print("D(Y) = ", autoCorrYnorm[0]) tauKX = 1 / autoCorrXnorm[0] tauKY = 1 / autoCorrYnorm[0] plt.figure(figsize=(12, 8)) plt.plot(autoCorrXnorm[:5]) plt.plot(autoCorrYnorm[:5]) plt.axhline(y=0.0, color='r') plt.axvline(x=tauKX, color='g') plt.axvline(x=tauKY, color='y') print('tau X', tauKX) print('tau Y', tauKY) plt.figure(figsize=(12, 8)) plt.plot(CorrXY[:50]) plt.axvline(x=CorrXY.index(max(CorrXY)), color='r') from scipy.fft import fft, fftfreq, rfft import matplotlib.pyplot as plt import numpy as np from matplotlib import collections as matcoll def speDencityPlt(X, T=1, color='b'): yf = fft(X) xf = fftfreq(len(X), T/len(X)) plt.figure(figsize=(12, 8)) for i in range(len(yf)): plt.vlines(xf[i], 0, abs(yf[i]), linestyles ="solid", colors ="b") plt.show() return yf, xf fAutoX, xfX = speDencityPlt(autoCorrXnorm) fAutoY, xfY = speDencityPlt(autoCorrYnorm) EnAutoX = 0 EnAutoY = 0 for c in fAutoX: EnAutoX = EnAutoX + abs(c)**2 EnAutoX = EnAutoX / 2 for c in fAutoY: EnAutoY = EnAutoY + abs(c)**2 EnAutoY = EnAutoY / 2 print("Энергия автокорреляции X:", EnAutoX) print("Энергия автокорреляции Y:", EnAutoY) import cmath fCorrXY, xfXY = speDencityPlt(CorrXY) phaseXY = [] for c in fCorrXY: phaseXY.append(cmath.phase(c)) plt.figure(figsize=(12, 8)) for i in range(len(phaseXY)): plt.vlines(xfXY[i], 0, abs(phaseXY[i]), linestyles ="solid", colors ="b") plt.show() |