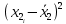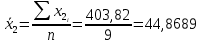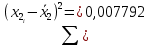чугуны. Отчет по лабораторной работе 3 Виды и методы измерения физических величин
 Скачать 225.65 Kb. Скачать 225.65 Kb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО «Алтайский государственный технический университет им. И.И. Ползунова» Кафедра «Детали машин» Работа защищена с оценкой __________ Преподаватель ___________________ (подпись) «___» _____________ 2020 г. дата Отчет по лабораторной работе № 3 «Виды и методы измерения физических величин» по дисциплине «Метрология, стандартизация и сертификация» ЛР03.23.05.01.07 Студент группы ТТС-82 Найденов М.Е. фамилия, и.о. Преподаватель Собачкин В.В. фамилия, и.о. БАРНАУЛ, 2020 Цель работы: ознакомление с основными видами и методами измерений физических величин, погрешностями измерений и их классификацией; обработкой результатов прямых и косвенных многократных измерений. Оборудование, технические средства измерения, расходные материалы: 1) деталь; 2) гладкий микрометр типа МК по ГОСТ 6507-90; 3) штангенциркуль по ГОСТ 166-89. Задание: Выполнить эскиз измеряемой детали. Выполнить замеры согласно эскизу. Произвести обработку результатов однократных и многократных (n=10) измерений. Результаты обработки занести в таблицы 1-4. Выполнение работы: 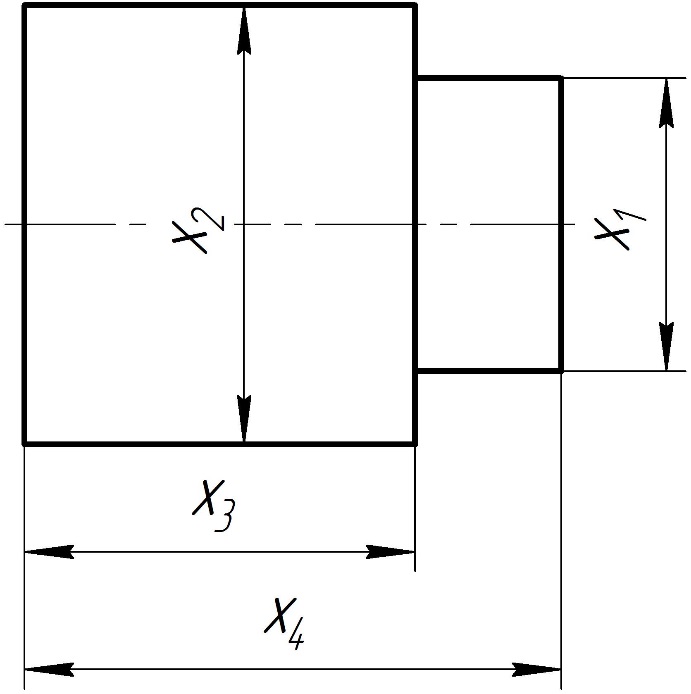 Рисунок 1 – Эскиз образца для измерений Таблица 1 – Результаты однократных измерений и расчетов
Таблица 2 – Результаты многократных измерений размеров х1 и х2
Проведем анализ полученных результатов измерений размера х1. Расположим результаты измерений в вариационный ряд по возрастанию: 30,01; 30,01; 30,03; 30,03; 30,03; 30,04; 30,09; 30,16; 30,20; 30,49. Д  адим графическую интерпретацию результатов измерений на числовой оси и покажем сомнительный результат измерения: Рисунок 2 – Графическая интерпретация на числовой оси результатов измерений размера х1 Оценим наличие промаха в измерениях по критерию Романовского: Среднее арифметическое без учета сомнительного числа: 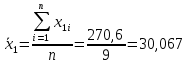 мм; мм;Оценка среднего квадратического отклонения без учета сомнительного числа 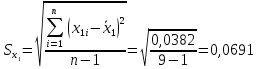 мм; мм;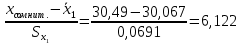 ; ;Критическое значение 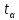 критерия Романовского при критерия Романовского при 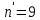 и и 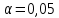 составляет составляет 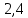 . . 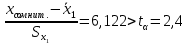 . Таким образом, значение измерения 30,49 является промахом и исключается из общей совокупности измерений. . Таким образом, значение измерения 30,49 является промахом и исключается из общей совокупности измерений.Таблица 3 – Результаты многократных измерений размера х1 и обработки результатов после исключения промаха
Продолжение таблицы 3
Для размера х1 выполним следующие действия: Оценка среднего квадратического отклонения результатов единичных измерений в ряду измерений: 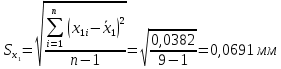 ; ;Оценка среднего квадратического отклонения результата измерения среднего арифметического: 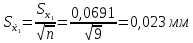 ; ;Границы доверительного интервала случайной погрешности без учета знака: 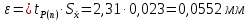 , где , где 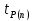 принято по таблице 4 для принято по таблице 4 для 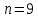 и и 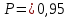 ; ;Границы неисключенной систематической погрешности (без учета знака) по ГОСТ 8.207-76 при вероятности 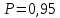 и и 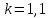 : :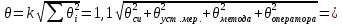 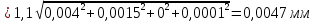 , где , где 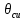 – предел допускаемой погрешности микрометра, – предел допускаемой погрешности микрометра, 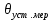 – погрешность установочной меры (определяется по таблице 3 для номинального размера 30 мм), – погрешность установочной меры (определяется по таблице 3 для номинального размера 30 мм), 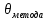 – погрешность метода непосредственной оценки и условий измерения, – погрешность метода непосредственной оценки и условий измерения, 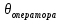 – погрешность оператора. – погрешность оператора.Соотношение неисключенной систематической погрешности 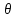 и среднего квадратического отклонения результата измерения и среднего квадратического отклонения результата измерения 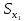 : : 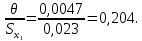 Выполняется условие Выполняется условие 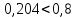 . Тогда границы погрешности результата измерения (без учета знака): . Тогда границы погрешности результата измерения (без учета знака): 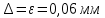 ; ;Окончательный результат: 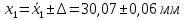 Проведем анализ полученных результатов измерений размера х2. Расположим результаты измерений в вариационный ряд по возрастанию: 44,81; 44,84; 44,85; 44,86; 44,88; 44,88; 44,89; 44,90; 44,91; 45,09. Д  адим графическую интерпретацию результатов измерений на числовой оси и покажем сомнительный результат измерения: Рисунок 2 – Графическая интерпретация на числовой оси результатов измерений размера х2 Оценим наличие промаха в измерениях по критерию Романовского: Среднее арифметическое без учета сомнительного числа: 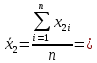 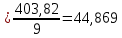 мм; мм;Оценка среднего квадратического отклонения без учета сомнительного числа 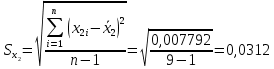 мм; мм;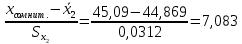 ; ;Критическое значение 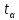 критерия Романовского при критерия Романовского при 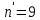 и и 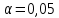 составляет составляет 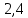 . . 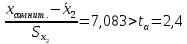 . Таким образом, значение измерения 45,09 является промахом и исключается из общей совокупности измерений. . Таким образом, значение измерения 45,09 является промахом и исключается из общей совокупности измерений.Таблица 4 – Результаты многократных измерений размера х2 и обработки результатов после исключения промаха
Для размера х2 выполним следующие действия: Оценка среднего квадратического отклонения результатов единичных измерений в ряду измерений: 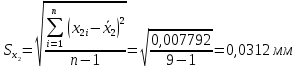 ; ;Оценка среднего квадратического отклонения результата измерения среднего арифметического: 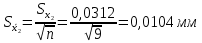 ; ;Границы доверительного интервала случайной погрешности без учета знака: 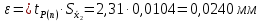 , где , где 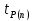 принято по таблице 4 для принято по таблице 4 для 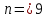 и и 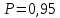 ; ;Границы неисключенной систематической погрешности (без учета знака) по ГОСТ 8.207-76 при вероятности 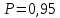 и и 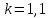 : :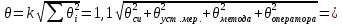 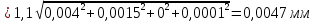 , где , где 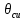 – предел допускаемой погрешности микрометра, – предел допускаемой погрешности микрометра, 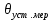 – погрешность установочной меры (определяется по таблице 3 для номинального размера 30 мм), – погрешность установочной меры (определяется по таблице 3 для номинального размера 30 мм), 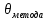 – погрешность метода непосредственной оценки и условий измерения, – погрешность метода непосредственной оценки и условий измерения, 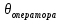 – погрешность оператора. – погрешность оператора.Соотношение неисключенной систематической погрешности 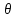 и среднего квадратического отклонения результата измерения и среднего квадратического отклонения результата измерения 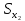 : : 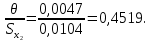 Выполняется условие Выполняется условие 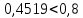 . Тогда границы погрешности результата измерения (без учета знака): . Тогда границы погрешности результата измерения (без учета знака): 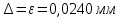 ; ;Окончательный результат: 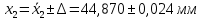 . .Вывод: в ходе выполнения лабораторной работы были изучены основные виды и методы измерений физических величин, погрешности измерений и их классификация. При проведении однократных измерений были получены следующие результаты: х1 = 30,040±0,004 мм; х2 = 44,880±0,004 мм; х3 = 40,450±0,004 мм; х4 = 54,9±0,1 мм. При проведении многократных измерений были получены следующие результаты: х1 = 30,07±0,06 мм; х2 = 44,870±0,024 мм. |

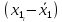 , мм
, мм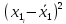
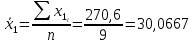
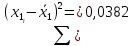
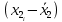 , мм
, мм