ТОЭ лаб1. Отчет по лабораторной работе 4 Исследование резонанса напряжений

Название	Отчет по лабораторной работе 4 Исследование резонанса напряжений
Анкор	ТОЭ лаб1.doc
Дата	07.05.2018
Размер	314 Kb.
Формат файла
Имя файла	ТОЭ лаб1.doc
Тип	Отчет #18960

Министерство образования и науки РФ

Томский Государственный Университет Систем Управления и Радиоэлектроники

(ТУСУР)
Кафедра ТОЭ
Отчет по лабораторной работе №4
«Исследование резонанса напряжений»

Выполнили:

студенты гр.420-1 Пичуева И.С

Демидова Ю.В

Проверил:

Коваленко В.Е.______

2012
ВВЕДЕНИЕ
Целью данной лабораторной работы является изучение физического смысла и условий наступления резонанса в последовательном RLС контуре, исследование в СМ МАРС поведения электрических переменных в резонансной и околорезонансной зоне при изменении параметров контура и анализ поведения этих же переменных в зависимости от частоты в зоне резонанса.

1 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Резонанс в последовательном контуре наступает при условии

Из этого условия можно сделать вывод, что резонанса в контуре можно достичь двумя способами:
1: Изменение и нахождение определенной резонансной частоты

при постоянных параметрах цепи;
2: Изменение и нахождение определенных параметров L и C при постоянной

;

В этих двух случаях достигается резонанс.
Для подтверждения первого пункта проводим эксперимент на установке показанной на рисунке 1.1
Изменяя частоту при постоянных параметрах цепи (C,L) , мы находим такое Wo , при котором амплитуда напряжения достигает максимального значения (максимум на осциллографе).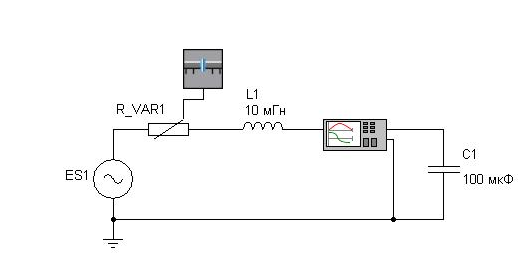

Рисунок 1.1 Схема эксперимента для нахождения резонансной частоты

где:

R_VAR1-активное сопротивление;

L1-индуктивность;

C1-емкость;

Ч- частотный настройщик (генератор);
Для подтверждения пункта второго строится цепь показанная на рисунке 1.2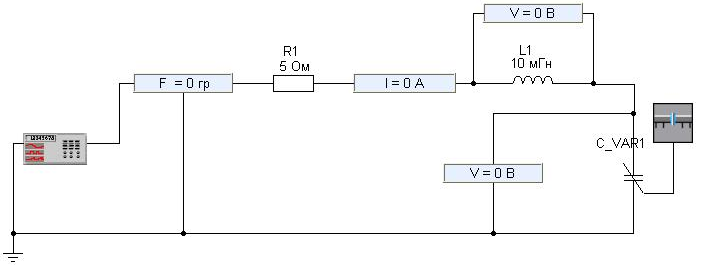

Рисунок 1.2 Схема для вычислительного эксперимента

Признаком резонанса является также отсутствие реактивного сопротивления, т.е угол между U и I должен быть равен = 0. Прибор F предназначен для определения

между U и I.На данной установке (рис. 1.2 ) устанавливаем резонансную частоту Wo , при которой сопротивление Xс на конденсаторе равно по модулю сопротивлению на индуктивности Xl и противоположно по знаку, т.е.

=0.Это должен зафиксировать прибор F.Затем изменяем емкость конденсатора и фиксируем параметры цепи.

Номер варианта	С	L	R
Номер варианта	Ф	Гн	Ом
4	0.0005	0.04	4

Таблица. 2.1 Значение начальных параметров цепи

2 ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Значение резонансной частоты:

(2.1)
Угол сдвига фаз между напряжением и током на входе цепи:

(2.2)

Значение тока установившегося при резонансе:

(2.3)

Значение сопротивления на индуктивности:

(2.4)
Значение сопротивления на емкости:

(2.5)

Значение добротности контура: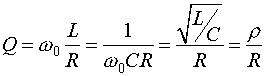

(2.6)
Характеристическое волновое сопротивление:

(2.7)
Величина затухания:

(2.8)

(2.9)
Полное сопротивление цепи Z:

(2.10)

Напряжения U_C₀ и U_L₀:

(2.11)

Полоса пропускания:

П=ω₀/Q (2.12)
Мощность:

Р=UI (2.13)

Падение напряжения на резисторе

U=I*R (2.14)

3 РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ

Находим резонансную частоту для данного контура по формуле (2.1):

f₀ =

(Гц)

= 223,607 с^-1

Найдем сопротивления на индуктивности и на емкости по формулам (2.4) и (2.5):

(Ом)

(Ом)

Находим ток в цепи I по формуле (2.3):

^-

Находим напряжения на индуктивности и емкости по формуле (2.11):

Найдем значение добротности по формуле (2.6):

Q=223,6*0,04/4= 2,236

Найдем значение полосы пропускания по формуле(2.12):

П=223,6*2,236=499,96 Рад/с

Найдем значение волнового сопротивления по формуле(2.7):

ρ=

=8,944 Ом

Находим значение мощности по формуле (2.13):

Экспериментальные данные, которые были установлены в ходе эксперимента показаны в таблице 3.1

U=10	ω_р	f_р	U_c	U_p	П	ρ	Q
B	Рад/с	кГц	В	А	Рад/с	Ом
Предварительный расчет	223,6	35,588	15,81	7,07	499,96	8,944	2,236
Вычислительный эксперемент	222	31,86	17,308

Таблица 3.1 Экспериментальные данные

Токи в цепи и напряжения на ее элементах для режимов представлены в таблице 3.2

Данные анализа на ПЭВМ						ПараметрС
U	I,мА	φ	U_L	U_C	Режим		Значение
7,07	207	-0,07	1,479	11,583	C1		C1=0.00005
7,07	2515	0	23,373	23,373	C2=Cрез		C2=0.0005
7,07	1124	0,5	11,583	1,479	C3>Cрез		C3= 0.005

Таблица 3.2 Режимы расчетов

Найдем сопротивления на индуктивности и на емкости по формулам (2.4) и (2.5):

(Ом)

(Ом)

Находим ток в цепи I по формуле (2.3):

Находим напряжения на индуктивности и емкости по формуле (2.11):

Результаты приведенных выше расчетов занесем в таблицу 3.3

U	ω₀	R	X_L₀	X_C₀	Z₀	I₀	U_L₀	U_C0	Q
В	рад/c	Ом	Ом	Ом	Ом	А	В	В
7,07	223,6	4	8,944	8,944	4	1,768	15,81	15,81	2,236

Таблица 3.2 Результаты расчета

Для заполнения таблицы 3.4 проведем расчеты по уже имеющимся формулам

Значения для C1:

Находим значения Xc (формула 2.5):

Ом

Находим значения

(формула2.4):

Ом

Находим значение общего сопротивления цепи (формула 2.10):

Ом

Находим силу тока в цепи (формула 2.3):

А

Находим падение напряжения на индуктивности(формула2.11):

U_L=89,44*0.087=7,84 В

Находим падение напряжения резисторе (формула2.14):

U_R=0.087*4=0.35 В

Находим мощность источника(формула 2.13):

P=7.07*0.087=0.615 Вт

Находим фазу между током и напряжением (формула3.2):

^о

Находим те же величины для С3:

Находим значения Xc (формула 2.5):

Ом

Находим значения

(формула2.4):

Ом

Находим значение общего сопротивления цепи (формула 2.10):

Ом

Находим силу тока в цепи (формула 2.3):

А

Находим падение напряжения на индуктивности(формула2.11):

U_L=0,89*0.785=0,698 В

Находим падение напряжения резисторе (формула2.14):

U_R=0.785*4=3,142 В

Находим мощность источника(формула 2.13):

P=7.07*0.785=5,54 Вт

Находим фазу между током и напряжением (формула3.2):

^о

Режим	U	I	C	X_С	X_L	Z	U_L	U_R	P	φ =atg(X/R)
Режим	В	А	Ф	Ом	Ом	Ом	В	В	Вт	φ
C1	4	0.087	0,00005	89,44	8,944	80,6	7,84	0,35	0,615	87,15
C2	4	1,768	0,0005	8,68	8,944	4	15,81	4	4,2	0,004
C3	4	0.785	0,005	0,89	8,944	9	0,698	3,142	5,54	63,5

Таблица 3.4 Результаты расчета

В таблице 4.4 дана зависимость падения напряжений на элементах цепи,фазы,тока от частоты.

ω	U_L	U_C	U_R	φ	I
Рад/с	B	В	В	Градусы	мА
100	1,715	8,575	1,567	-76	0,43
200	12,649	15,811	4,311	-26,5	1,581
500	8,575	1,715	3,162	76	0,4
1000	7,402	0,37	1,265	84	0,185
1500	7,215	0,16	0,813	86	0,012
2000	7,115	0,894	0,599	87	0,894
2500	7,112	0,57	0,417	87,6	0,712
3000	7,107	0,395	0,395	88	0,592
4000	7,091	0,221	0,295	88,5	0,443

Таблица 4.4

На основани даных таблицы 4.4 можно построить графики зависимости I=f(w), U_C=f(w) ,U_L=f(w)

U_R=f(w), φ=f(w) C⁰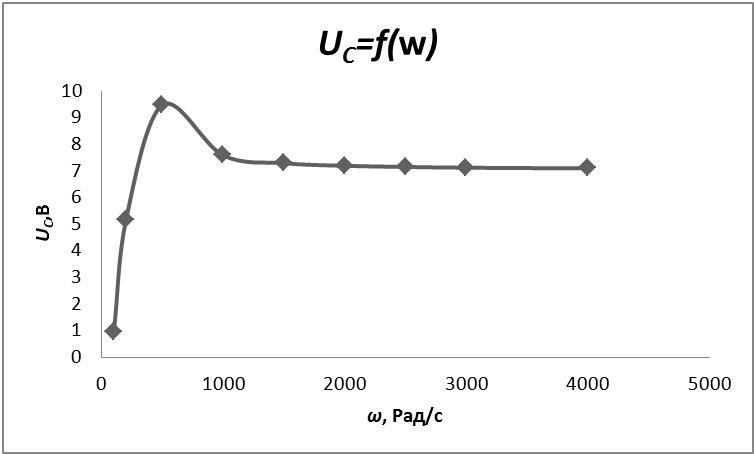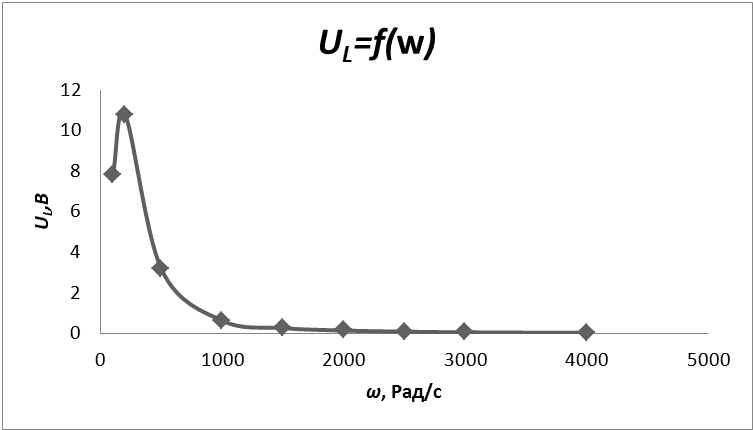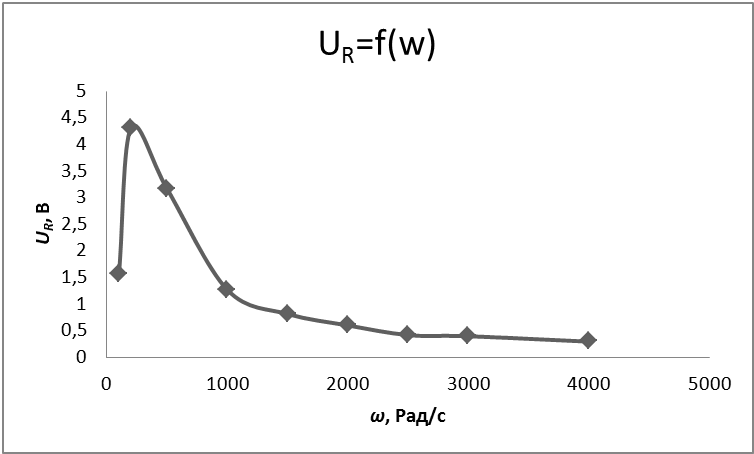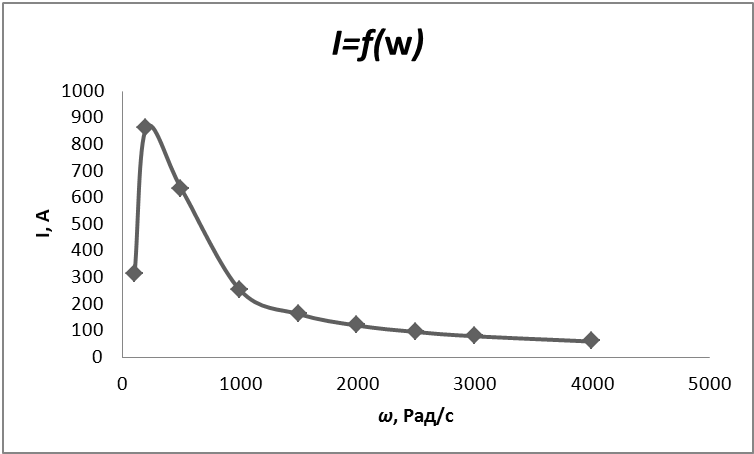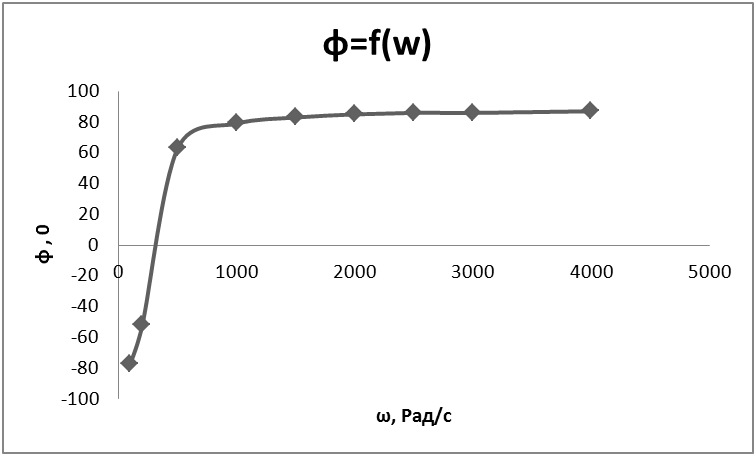

Контрольные вопросы

1. В чем причина наступления резонанса напряжений, и каковы характеризующие его соотношения?

Ответ: Если подобрать элементы L и C таким образом, чтобы их сопротивления стали равными (X_L=X_C), то индуктивное сопротивление станет равно нулю и общее сопротивление станет минимальным, а следовательно ток будет максимален. При резонансе U_L=U_C, X_L=X_C>>R, I=E/R, ω₀=(LC)^1/2– резонансная частота.
2. Как можно управлять резонансом?

Ответ: Изменять частоту при неизменных параметрах или изменять параметры L и C при частоте = const.

3. Какие режимы анализа необходимо использовать для получения временных и частотных характеристик?

Ответ: Для получения частотных характеристик необходимо установить зависимоть напряжения на резисторе от частоты W U_r=

.Для получения временных характеристик необходимо установить зависимость Ur ,Ul , Uc,I от времени при W=const.