Отчет по лабораторной работе 5 по дисциплине Цифровые методы формирования и обработки сигналов в итс

• Название: Отчет по лабораторной работе 5 по дисциплине Цифровые методы формирования и обработки сигналов в итс
• Анкор: lab5rrrrqq22
• Дата: 29.03.2023
• Размер: 187.11 Kb.
• Имя файла: Lab5_12001852_Hizhnyack.docx
• Тип: Отчет; #1024544

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОКОММУНИКАЦИОННЫХ ТЕХНОЛОГИЙ И СИСТЕМ СВЯЗИ

Отчет по лабораторной работе № 5

по дисциплине: «Цифровые методы формирования и обработки сигналов в ИТС»

Тема работы: «Квантование по уровню»
студента заочного отделения

5 курса 12001852 группы

Хижняка Юрия Павловича

Проверил:

Проверил: доцент кафедры ИТСиТ

Балабанова Татьяна Николаевна


БЕЛГОРОД, 2023

Цель работы:
Общая постановка задачи:

1. Выбрать N отсчетов сигнала x₃(t) из лабораторной работы №5.

2. Осуществить квантование по уровню при m=1; 2; 3; 4 разрядов квантования.

3. В каждом случае восстановить исходный сигнал по квантованным значениям.

4. Для каждого из случаев определить ошибку квантования. Построить график зависимости ошибки квантования от числа разрядов.

5. Сделать выводы по проделанной работе.
Результаты выполнения работы

1. 
   Осуществим квантование по уровню сигнала х3, при m=1; 2; 3; 4.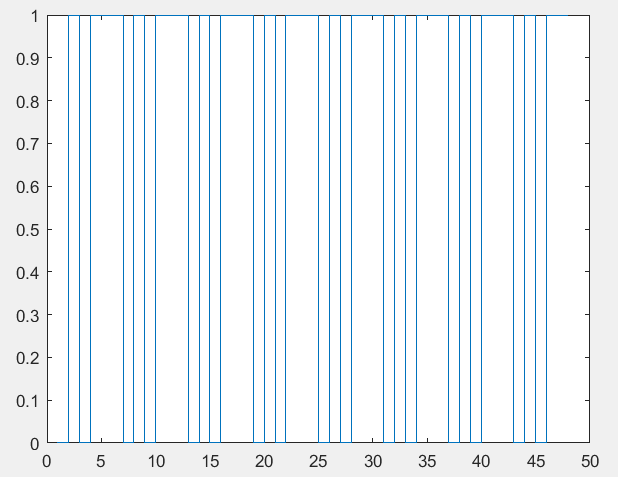
   

Рисунок_1_–_Квантованный_сигнал,_m_=_1_.'>Рисунок 1 – Квантованный сигнал, m=1.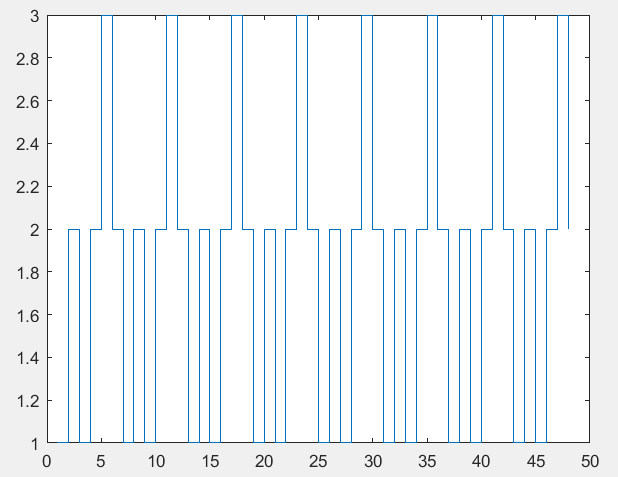



Рисунок 2 – Квантованный сигнал, m=2.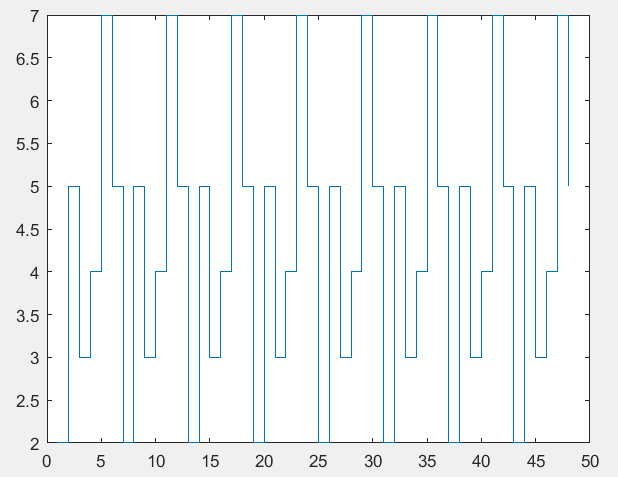



Рисунок 3 – Квантованный сигнал, m=3.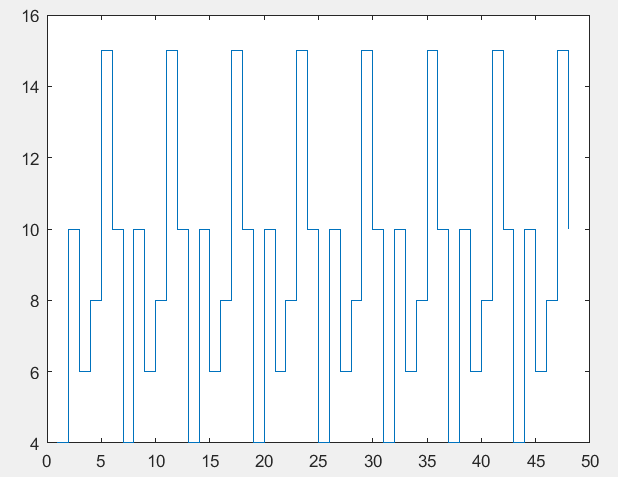



Рисунок 4 – Квантованный сигнал, m=4.

2. 
   Восстановим исходный сигнал по квантованным значениям.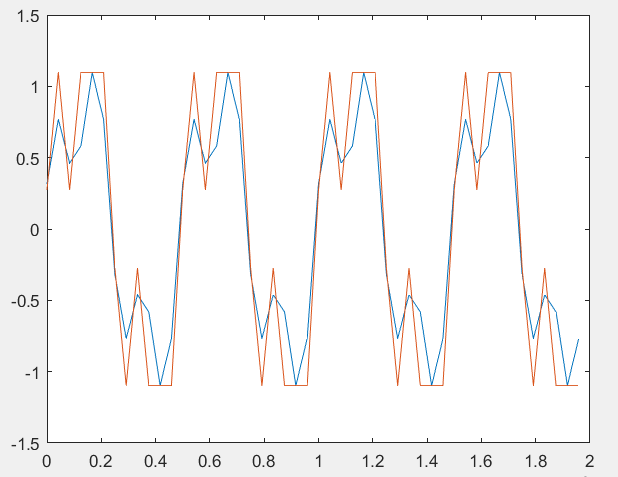
   

Рисунок 5– Восстановленный сигнал, m=1; ee=0.4137.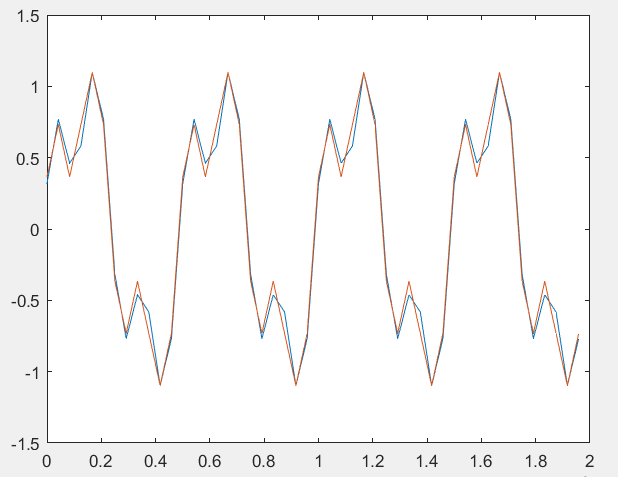



Рисунок 6 – Восстановленный сигнал, m=2; ee=0,1096.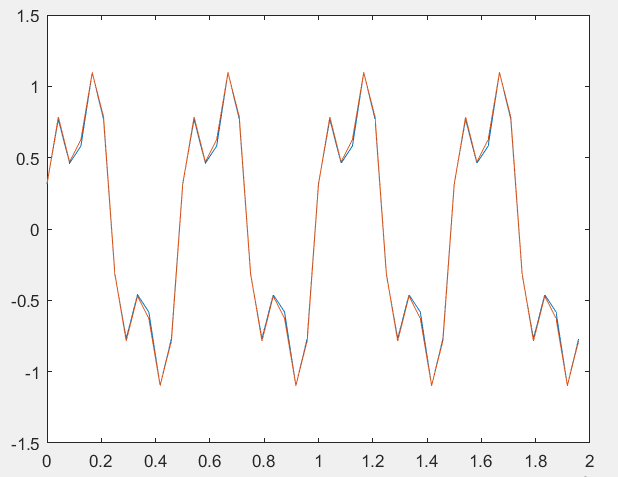


Рисунок 7 – Восстановленный сигнал, m=3; ee=0,0296.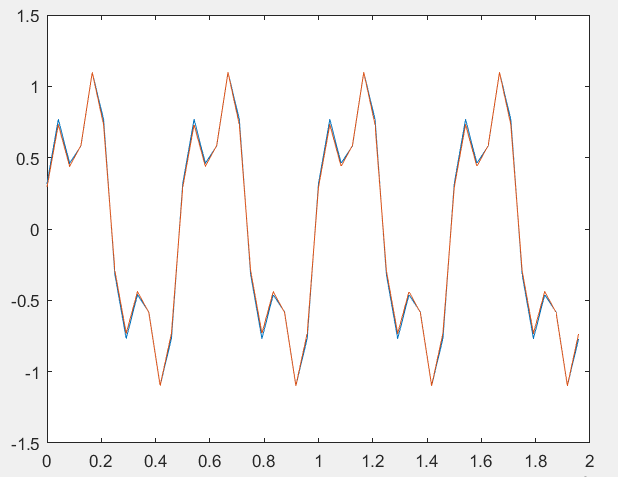



Рисунок 8 – Восстановленный сигнал m=4; ee=0,0354.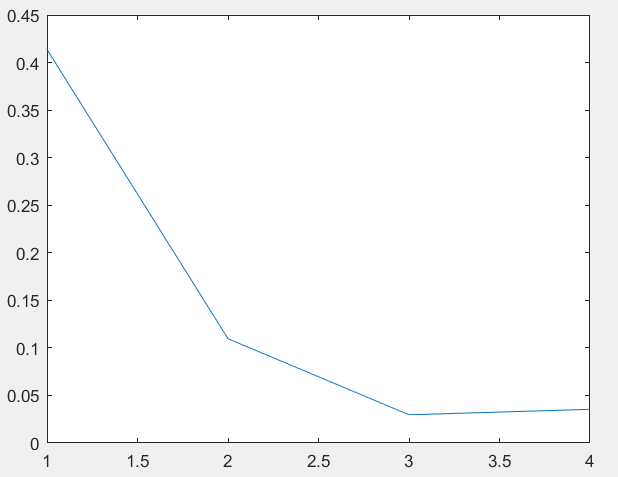



Рисунок 9 – График зависимости ошибки квантования от количества разрядов квантования.

Вывод:

По результатам, которые были получены при выполнении лабораторной работы очевидно, что большее количество разрядов квантования позволяет лучше восстановить сигнал по кантованным значениям. Также данный вывод подтверждают рассчитанные в ходе работы ошибки квантования.

ПРИЛОЖЕНИЕ 1
Листинг программы

clear;

clc;

f1=8000;

Fd=12*f1;

T=1/f1;

Td=1/Fd;

n=T/Td;

N=4*n;

fi=0*pi;

t=[1e-15:Td:T*N/n];

Xm=2.6;

x1=Xm*sin((2*pi*f1)*t+fi);

f2=3*f1;

Xm2=1/2*Xm;

fi2=pi/4;

x2=Xm2*sin((2*pi*f2).*t+fi2);

x3=x1+x2;

zn = sign(x3);
X3_max = max(abs(x3));


m1 = 1; % вектор чисел разрядов квантования

% Осуществим квантование сигнала х3 для одного уровня квантования

N1_quan = 2^m1-1; % число уровней квантования

del1 = 1/N1_quan; % шаг квантования

for i=1:length(x3)

S1_quan(i) = floor(((abs(x3(i)))/(X3_max*del1)) + 0.5); % квантованный сигнал

end

for i=1:length(S1_quan)

if S1_quan(i) == 0

d1(i) = 0.25;

else d1(i) = 0;

end

end

for i=1:length(S1_quan)

X3_BoccTaHoB1(i) = zn(i)*(S1_quan(i)+d1(i))*X3_max*del1; % восстановление сигнала

end

figure(1), stairs(S1_quan)

figure(2), plot (t, x3, t, X3_BoccTaHoB1)

D_x3_1 = sqrt(sum((X3_BoccTaHoB1-x3).^2)/(sum((x3).^2))); %ошибка квантования

% Проделаем эти же действия для двух разрядов квантования

m2 = 2;

N2_quan = 2^m2-1;

del2 = 1/N2_quan;

for i=1:length(x3)

S2_quan(i) = floor(((abs(x3(i)))/(X3_max*del2)) + 0.5);

end

for i=1:length(S2_quan)

if S2_quan(i) == 0

d2(i) = 0.25;

else d2(i) = 0;

end

end

for i=1:length(S2_quan)

X3_BoccTaHoB2(i) = zn(i)*(S2_quan(i)+d2(i))*X3_max*del2;

end

figure(3), stairs(S2_quan)

figure(4), plot (t, x3, t, X3_BoccTaHoB2)

D_x3_2 = sqrt(sum((X3_BoccTaHoB2-x3).^2)/(sum((x3).^2)));

% Проделаем эти же действия для трех разрядов квантования

m3 = 3;

N3_quan = 2^m3-1;

del3 = 1/N3_quan;

for i=1:length(x3)

S3_quan(i) = floor(((abs(x3(i)))/(X3_max*del3)) + 0.5);

end

for i=1:length(S3_quan)

if S3_quan(i) == 0

d3(i) = 0.25;

else d3(i) = 0;

end

end

for i=1:length(S3_quan)

X3_BoccTaHoB3(i) = zn(i)*(S3_quan(i)+d3(i))*X3_max*del3;

end

figure(5), stairs(S3_quan)

figure(6), plot (t, x3, t, X3_BoccTaHoB3)

D_x3_3 = sqrt(sum((X3_BoccTaHoB3-x3).^2)/(sum((x3).^2)));

% Проделаем эти же действия для четырех разрядов квантования

m4 = 4;

N4_quan = 2^m4-1;

del4 = 1/N4_quan;

for i=1:length(x3)

S4_quan(i) = floor(((abs(x3(i)))/(X3_max*del4)) + 0.5);

end

for i=1:length(S4_quan)

if S4_quan(i) == 0

d4(i) = 0.25;

else d4(i) = 0;

end

end

for i=1:length(S4_quan)

X3_BoccTaHoB4(i) = zn(i)*(S4_quan(i)+d4(i))*X3_max*del4;

end

figure(7), stairs(S4_quan)

figure(8), plot (t, x3, t, X3_BoccTaHoB4)

D_x3_4 = sqrt(sum((X3_BoccTaHoB4-x3).^2)/(sum((x3).^2)));

% Построим график зависимости ошибки квантования от числа разрядов

D = [D_x3_1, D_x3_2, D_x3_3, D_x3_4];

m = [m1 m2 m3 m4];

figure(9), plot(m, D)