Машинное обучение ЛР№5. МО ЛР5 Логинов О-5КМ91. Отчёт по лабораторной работе 5
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
Подразделение: Инженерная школа энергетики Направление подготовки: 09.04.03 – Прикладная информатика Отделение: Электроэнергетики и электротехники Кластеризация отчёт по лабораторной работе №5 Вариант 7 по дисциплине: «Машинное обучение»
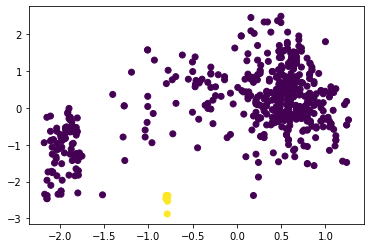
Томск 2021 Цель работы: написать программу на Python, которая выполняет алгоритм кластеризации. Задачи работы: В качестве набора данных выбрать один из рассмотренных ранее на других лабораторных работах. Выбрать два произвольных численных признака для кластеризации. При необходимости привести признаки к стандартному масштабу. Использовать алгоритмы кластеризации: K-means, агломеративная кластеризация и DBScan. Провести эксперимент по выявлению оптимального количества кластеров, для каждого результата вывести метрику качества, показать на графике кластеры и центроиды для каждого алгоритма и их гиперпараметров. Выбрать лучшее сочетание алгоритма и гиперпараметров, сделать выводы и отразить в отчёте. Ход работы В качестве набора данных был выбран датасет forestfires.csv из ЛР4. Для датасета был построен pairplot с целью выявления двух наиболее пригодных для кластеризации признаков (рисунок 1). 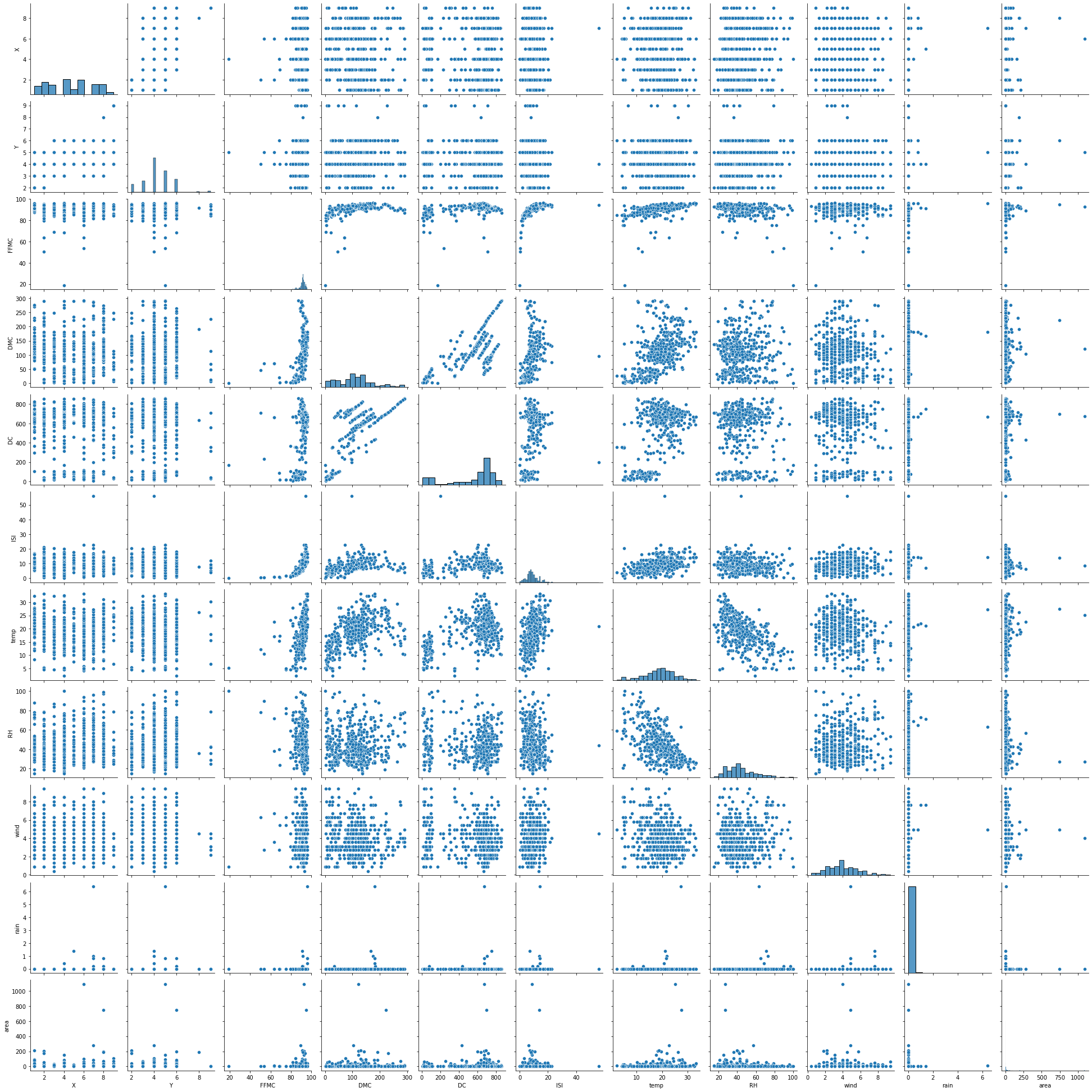 Рисунок 1 – Pairplot для датасета forestfires.csv Для дальнейшей работы была выбрана пара признаков DC (индекс засухи) и temp (температура) (рисунок 2). 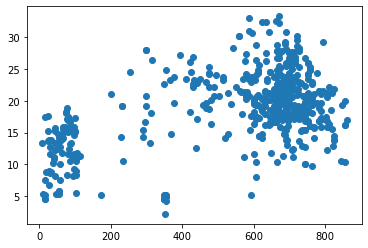 Рисунок 2 – Распределение значений Перед рассмотрением работы алгоритмов кластеризации произведём стандартизацию данных (листинг 1) Листинг 1
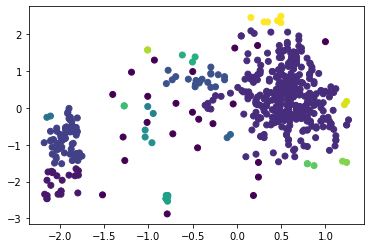
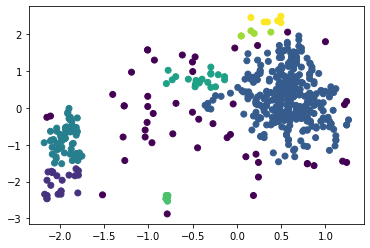
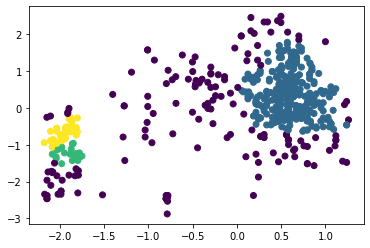
Исследуем алгоритм K-средних, зададим число кластеров, равное трём (листинг 2, рисунок 3). Листинг 2
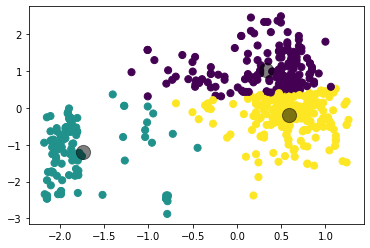 Рисунок 3 – Результат работы алгоритма K-means Определим силуэтные коэффициенты для количества кластеров от 2 до 8, листинг и результаты представлены на рисунках ниже. Листинг 3
 Рисунок 4 – Коэффициенты силуэта для различного количества кластеров по алгоритму K-means 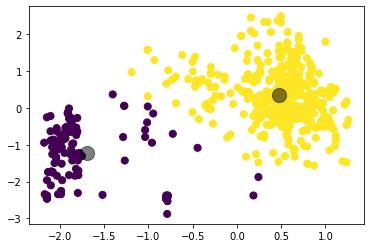 Рисунок 5 – Визуализация двух кластеров по алгоритму K-means 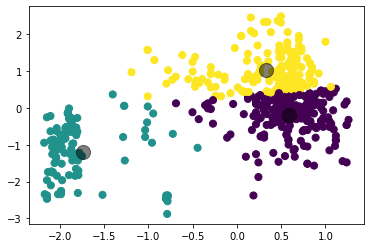 Рисунок 6 – Визуализация трёх кластеров по алгоритму K-means 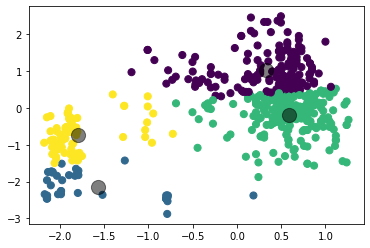 Рисунок 7 – Визуализация четырёх кластеров по алгоритму K-means 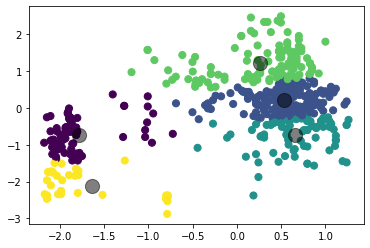 Рисунок 8 – Визуализация пяти кластеров по алгоритму K-means 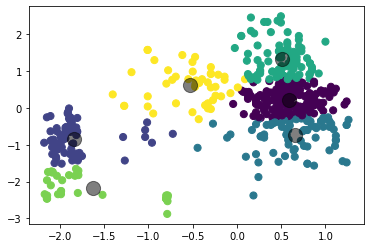 Рисунок 9 – Визуализация шести кластеров по алгоритму K-means 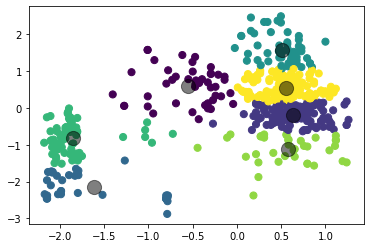 Рисунок 10 – Визуализация семи кластеров по алгоритму K-means 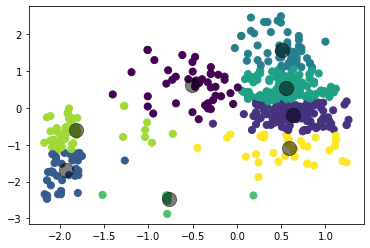 Рисунок 11 – Визуализация восьми кластеров по алгоритму K-means Как видно, наибольшее значение силуэтного коэффициента получено при двух кластерах. Далее определим оптимальное число кластеров по методу локтя. Для этого построим график зависимости искажения (внутрикластерной суммы квадратичных ошибок) от числа кластеров (листинг 4, рисунок 12). Листинг 4
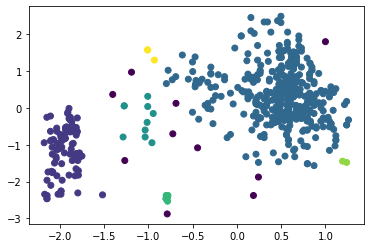
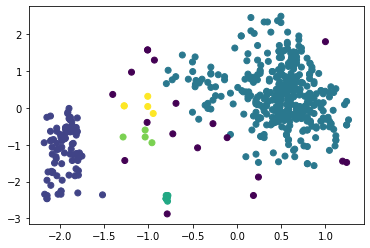
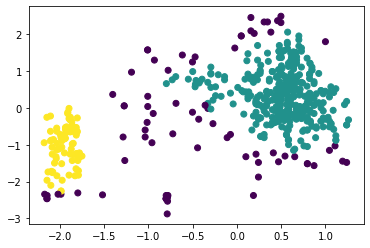
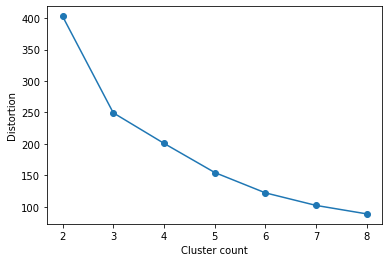 Рисунок 12 – График искажения для разных значений числа кластеров Согласно методу локтя, оптимальным числом кластеров является то, при котором искажение начинает увеличиваться быстрее всего. Как видно на рисунке 12, «локоть» расположен в точке k = 3, то есть для данного набора данных такое число кластеров может быть хорошим вариантом. Рассмотрим далее алгоритм агломеративной кластеризации при количестве кластеров, равном трём (листинг 5, рисунок 13). Листинг 5
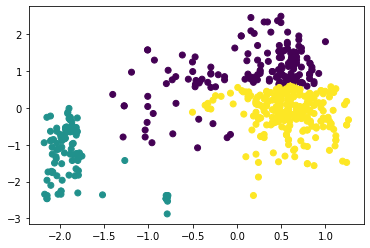 Рисунок 13 – Результат работы алгоритма агломеративной кластеризации Определим коэффициент силуэта для количества кластеров от 2 до 8, листинг и результаты представлены на рисунках ниже. Листинг 6
 Рисунок 14 – Коэффициенты силуэта для различного количества кластеров по алгоритму агломеративной кластеризации 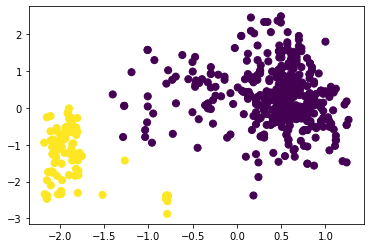 Рисунок 15 – Визуализация двух кластеров по алгоритму агломеративной кластеризации 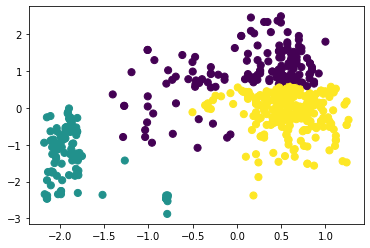 Рисунок 16 – Визуализация трёх кластеров по алгоритму агломеративной кластеризации 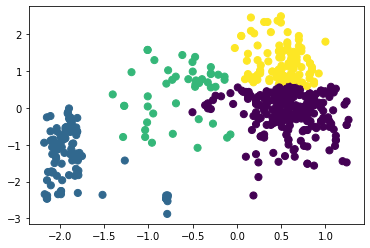 Рисунок 17 – Визуализация четырёх кластеров по алгоритму агломеративной кластеризации 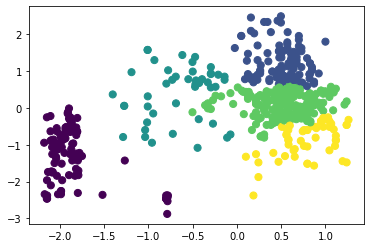 Рисунок 18 – Визуализация пяти кластеров по алгоритму агломеративной кластеризации 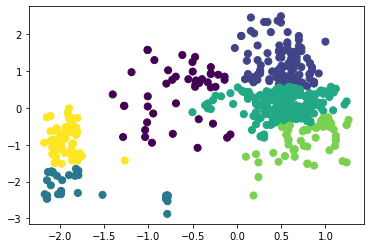 Рисунок 19 – Визуализация шести кластеров по алгоритму агломеративной кластеризации 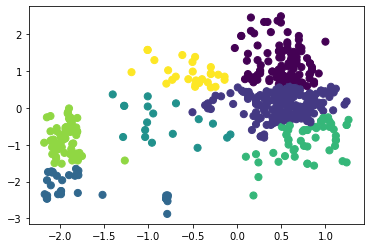 Рисунок 20 – Визуализация семи кластеров по алгоритму агломеративной кластеризации 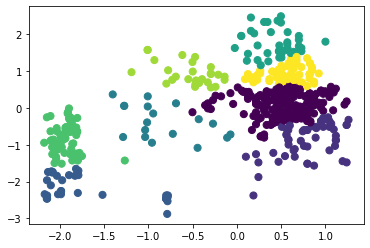 Рисунок 21 – Визуализация восьми кластеров по алгоритму агломеративной кластеризации Как и в случае с алгоритмом К-средних, наибольшее значение коэффициента получено при числе кластеров, равном двум. Рассмотрим далее алгоритм DBScan. В таблице 1 представлена зависимость результатов работы алгоритма от параметров eps и min_samples. Таблица 1 – Результаты работы алгоритма DBScan в зависимости от значений гиперпараметров
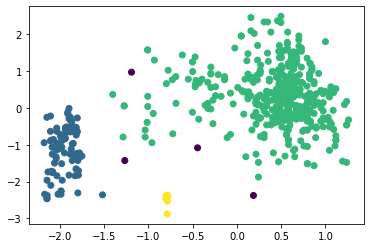
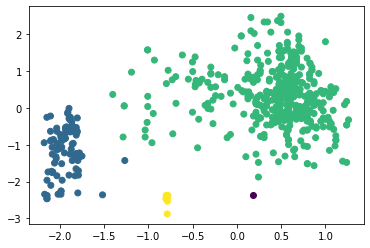
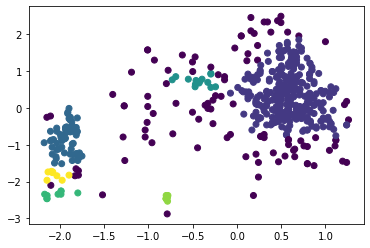
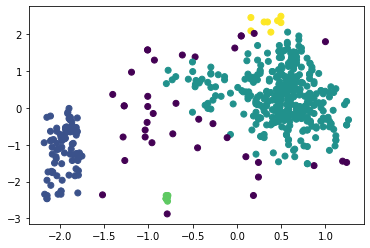
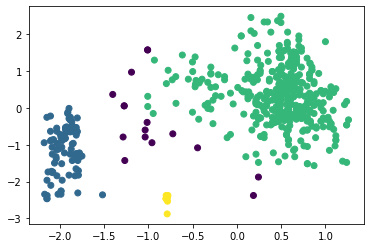
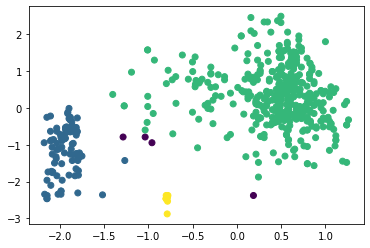
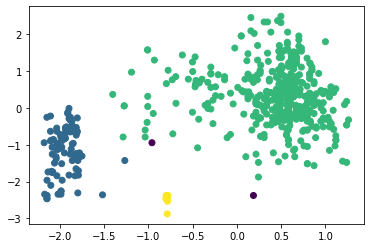
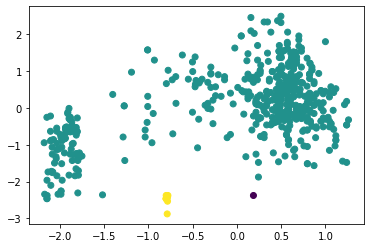
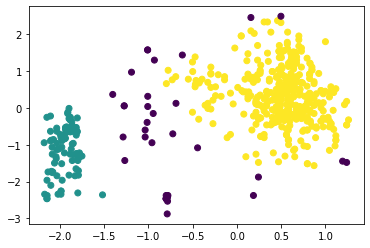
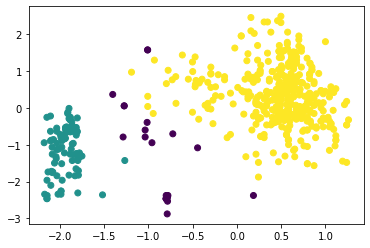
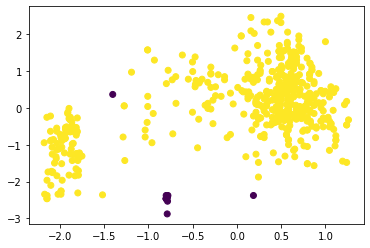
Наибольшее полученное значение коэффициента силуэта равно 0,5734 при eps = 0,53 и min_samples = 4 (листинг 7, таблица 1). При этом можно отметить, что алгоритм поделил исследуемый набор данных на три кластера достаточно точно (рисунок 22). Листинг 7
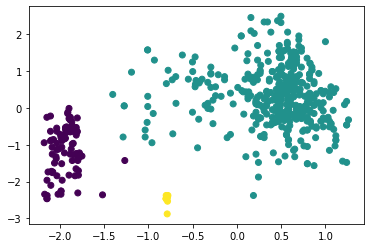 Рисунок 22 – Разделение на три кластера алгоритмом DBScan Вывод В результате выполнения работы написана программа на Python, которая выполняет кластеризацию по методу К-means, агломеративной кластеризации и DBScan. Путём оценки силуэтного коэффициента было выявлено, что наибольшее его значение имеет место при двух кластерах (для алгоритмов К-средних и агломеративной кластеризации), однако оценка по методу локтя показала, что оптимальным количеством кластеров является 3 (что больше соответствует действительности). При исследовании алгоритма DBScan было получено наилучшее сочетание гиперпараметров, при котором коэффициент силуэта для трёх кластеров составил 0,574, в то время как для алгоритмов K-means и агломеративной кластеризации он равен 0,453 и 0,436 соответственно. Полученный результат можно считать оптимальным, к тому же, он наилучшим образом иллюстрирует разделение на три кластера. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||