ПДС лаба 3. Лаба 3. Отчет. Отчет по лабораторной работе дисциплины Передача дискретных сообщений

• Название: Отчет по лабораторной работе дисциплины Передача дискретных сообщений
• Анкор: ПДС лаба 3
• Дата: 11.11.2022
• Размер: 0.78 Mb.
• Имя файла: Лаба 3. Отчет.docx
• Тип: Отчет; #782542

Министерство цифрового развития, связи и массовых коммуникаций РФ

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет телекоммуникаций и

информатики»

(СибГУТИ)

Кафедра инфокоммуникационных систем и сетей (ИКСС)
10.05.02 Информационная
безопасность телекоммуникационных
систем, специализация Защита
информации в системах связи и
управления - ВУЦ

(очная форма обучения)
отчет по лабораторной работе

дисциплины «Передача дискретных сообщений»

Эффективное кодирование на примере кода Хаффмена
Выполнил:

студент ИБ,

гр. АБ-016 / Н. А. Сакулян/

«__»_________ 2022 г. (подпись)
Проверил:

Преп. каф. ИКСС / Д. Д. Калмыкова/

«__»_________ 2022 г. (подпись)
Новосибирск 2022

Цель работы: Изучение принципа эффективного кодирования источника дискретных сообщений.
Домашнее задание:

1. 
   Изучить принцип эффективного кодирования источника дискретных сообщений (метод Хаффмена)
   
2. 
   Осуществить кодирование каждого сообщения алфавита, данного в виде таблицы, используя двоичный код:
   

• 
  Равномерный;
  
• 
  Код Хаффмена, в соответствии с заданным вариантом.
  

3. 
   Определить значения Hmax(x), H (x) и l3
   
4. 
   Рассчитать значения Ксс и Коэ.
   

Результаты выполнения домашней работы: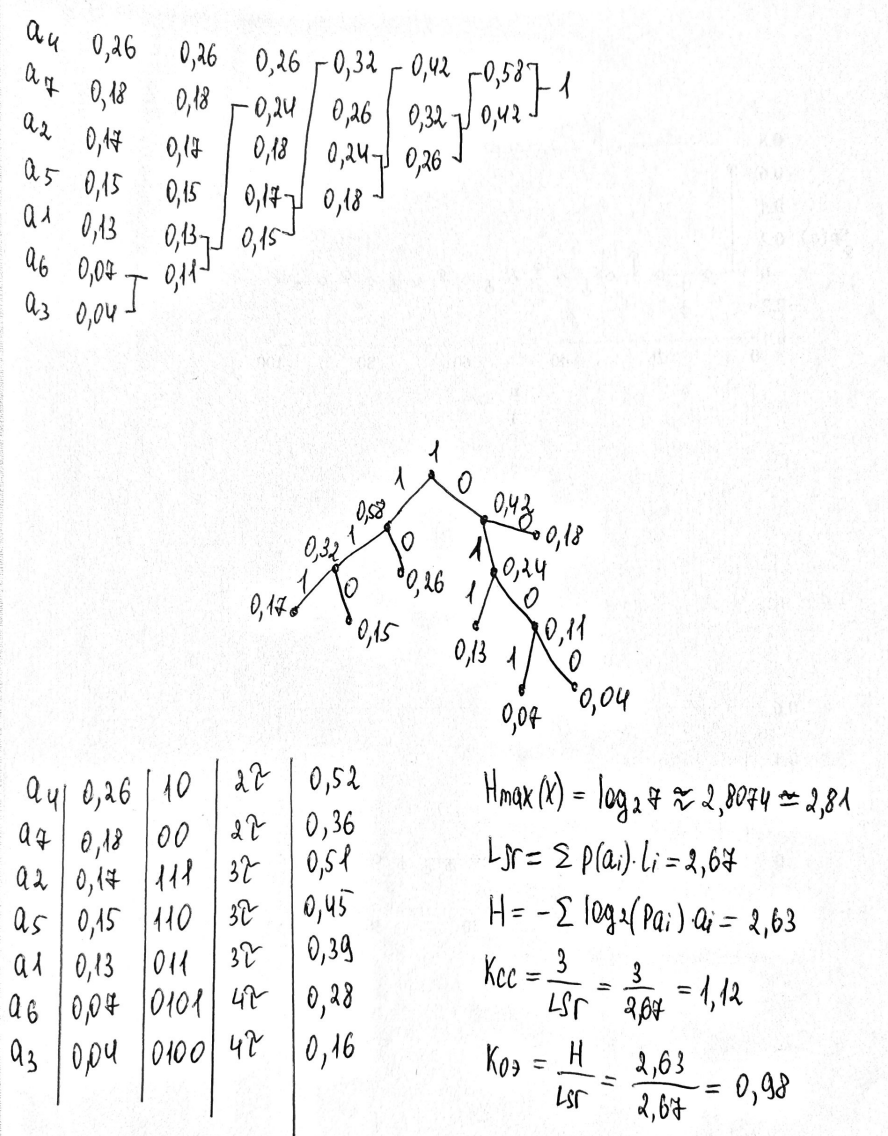



Рисунок 1.1 Результат выполнения домашней работы

Результаты выполнения лабораторной работы

Задание 1:

Проверка результатов расчетов домашнего задания.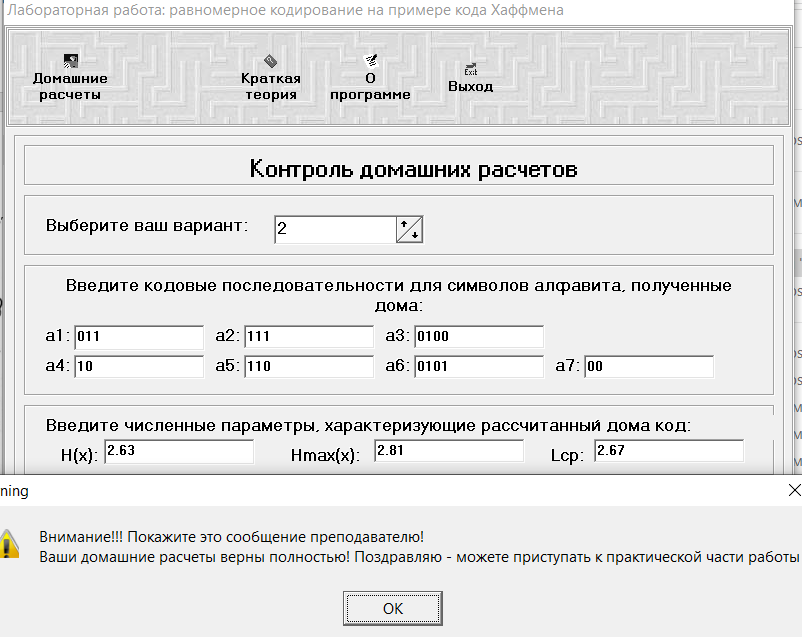


Рисунок 2.2 Контроль домашних расчетов
Все результаты верны, приступаем к лабораторной работе.
Задание 2:

Определение средней длины сообщения при передаче последовательностей, составленных из сообщений, имеющих разную вероятность появления.

После открытия окна ввода, выставляем алфавит из домашнего задания. Далее составим три последовательности по заданию. Вводим их и смотрим среднюю длину кодовой комбинации на сообщение алфавита при равномерном и эффективном кодировании.



Рисунок 3.3 Чередование двух наиболее вероятных сообщений (a4, a7)


Рисунок 4.4 Рассчитанное по формуле значение: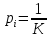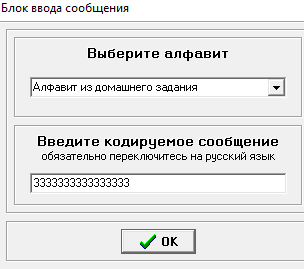


Рисунок 5.5 Сообщение с минимальной вероятностью появления (a3)

Вывод по заданию 2: при кодировании равномерным кодом средняя длина символа последовательности не зависит от вероятностей символов. При кодировании кодом Хаффмена средняя длина последовательности с уменьшением вероятностей сообщений увеличивается, т.е. чем менее вероятное сообщение, тем большей длины потребуется символ для кодировки.
Задание 3:

Исследование влияния одиночной ошибки на результаты декодирования.

Составляем и вводим произвольную комбинацию из 16 сообщений. Далее в блоке ввода ошибки изменяем элемент на противоположный, инвертируем.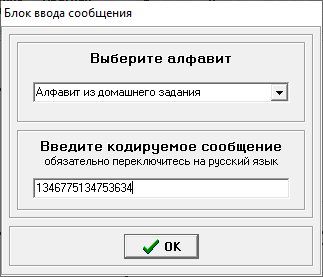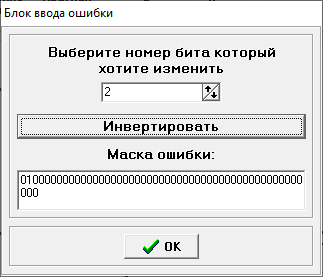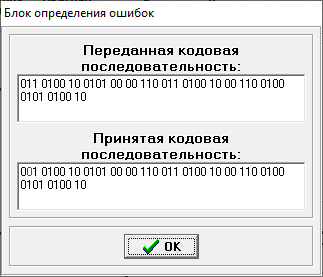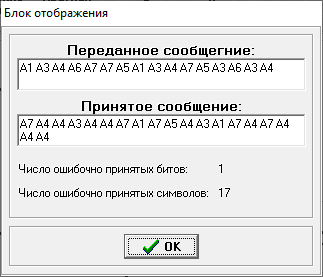



Рисунок 6.6 Результаты выполнения операций
Промежуточные выводы: мы изменили второй элемент, поменялась последовательность. В итоге это полностью повлияло на принятое сообщение, оно совершенно отличается от исходного.

Далее устанавливаем для ввода русский алфавит, вводим последовательность слов, состоящих из количества, равное или меньше 24.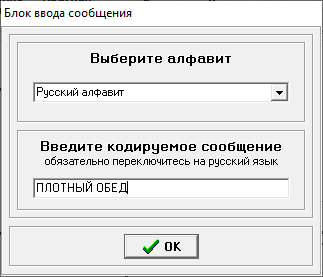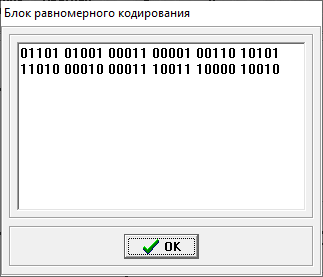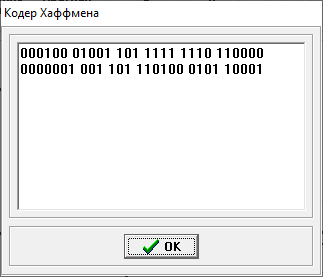



Рисунок 7.7 Результаты выполнения операций
Сравним количество двоичных символов, необходимых для передачи введенного текста при кодировании равномерным кодом и кодом Хаффмена. При равномерном кодировании это число составляет 60, а при Хаффмене 56.

Можем сделать вывод, что количество двоичных символов при кодировании кодом Хаффмана меньше, чем при кодировании равномерным кодом. Это говорит о том, что число символов, имеющих большую вероятность, больше, чем число символов с меньшей вероятностью. Если бы количество двоичных символов при кодировании кодом Хаффмана было бы больше, чем при кодировании равномерным кодом, то число символов с меньшей вероятностью было бы больше, чем число символов с большей вероятностью.

Вводим ошибку в единичный элемент, соответствующий варианту. Далее смотрим как расшифровывается последовательность.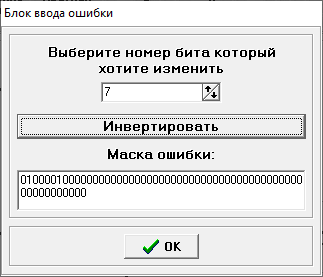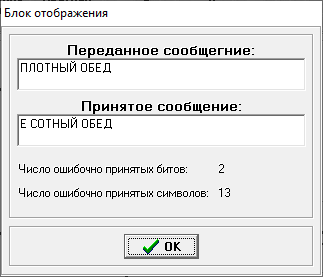



Рисунок 8.7 Результаты выполнения операций

В связи с тем, что мы ввели ошибку, принятое сообщение снова выдается неправильно.

Выводы по работе:

В дополнение к промежуточным выводам в работе, стоит отметить следующее.

Можно выделить следующие недостатки метода Хаффмена. Когда вероятность символов для входных данных неизвестна, статические коды Хаффмена работают неэффективно. Еще один недостаток кодов Хаффмена — это то, что минимальная длина кодового слова для них не может быть меньше единицы, тогда как энтропия сообщения вполне может составлять и 0,1, и 0,01 бит/букву. В этом случае код Хаффмена становится существенно избыточным. аконец, код Хаффмена обеспечивает среднюю длину кода, совпадающую с энтропией, только в том случае, когда вероятности символов источника являются целыми отрицательными степенями двойки: 1/2 = 0,5; 1/4 = 0,25; 1/8 = 0,125; 1/16 = 0,0625 и т.д. На практике же такая ситуация встречается очень редко или может быть создана блокированием символов со всеми вытекающими отсюда последствиями.

Равномерные коды легче декодировать, но закодированные сообщения будут содержать больше символов. Сообщения, закодированные неравномерными кодами, будут короче, чем на равномерных кодах, но необходимо будет для кодирования сообщения проверять код на условие Фано, и закодированное сообщение сложнее раскодировать. Так же невозможно сразу посчитать количество символов, по сравнению с равномерными кодами.