ИССЛЕДОВАНИЕ ДИСКРЕТНЫХ СИГНАЛОВ ВО ВРЕМЕННОЙ ОБЛАСТИ. Отчет по лабораторной работе исследование дискретных сигналов во временной области по курсу общая теория связи
 Скачать 145.52 Kb. Скачать 145.52 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ» КАФЕДРА №52 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург, 2021 Вариант 2.4(Фазовая модуляция): 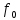 = 2400 Гц – несущая частота; = 2400 Гц – несущая частота;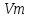 = 600 Бод – модуляционная скорость; = 600 Бод – модуляционная скорость;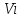 = 1200 бит/с – информационная скорость. = 1200 бит/с – информационная скорость.Цель работы Получение описания сигнального множества во временной и частотной модуляции. Построить графики всех сигналов Вычислить энергию всех сигналов Формулы для вычисления недостающих параметров 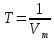 , (1.1) , (1.1)где T – период следования сигналов; 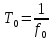 , (1.2) , (1.2)где 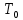 – период несущей частоты – период несущей частоты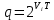 (1.3) (1.3)где q – количество сигналов; 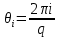 (1.4) (1.4)где 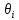 – начальная фаза. – начальная фаза.Вычисления недостающих параметров: 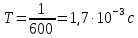 (1.1) (1.1)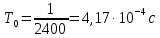 (1.2) (1.2)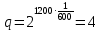 (1.3) (1.3)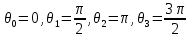 (1.4) (1.4)Приведение аналитического выражение для всех сигналов из множества как функций времени Сигналы дискретной фазовой модуляции задаются следующим образом: Si(t) = 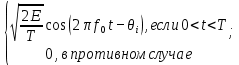 (2.1) Известно, что для любого i=0,1,2,…,q-1 выполняется условие 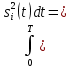 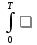 = E = E (2.2) Проверим выполнения условия: 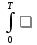 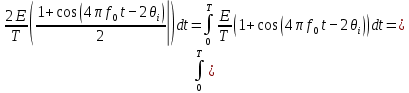 = 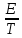 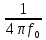 E + E + 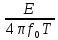 (2.3) Для первого сигнала 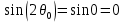 , ,для второго 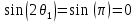 , , для третьего 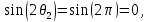 для четвертого 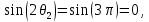 поэтому действует одно уравнение: поэтому действует одно уравнение: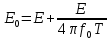 Следовательно энергии всех сигналов равны ( 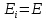 , что и требовалось доказать. , что и требовалось доказать.Вычисление значения энергии всех сигналов Пусть 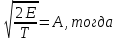 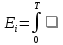 Пользуясь заменой переменных получаем, что: 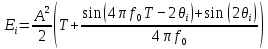 (3.1) (3.1)и полагаем, что A = 1. Вычисления: 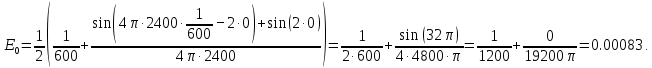 Данный результат совпадает с результатом, посчитанным в среде Matlab 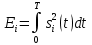 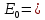 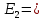 0.000837500000000000 0.000837500000000000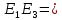 0.000833333333333333 0.000833333333333333 Погрешность вычислений: 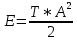 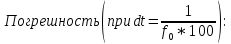 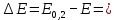 4.16 4.16 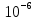 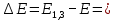 -1.08 -1.08 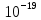 При увеличении шага дискретизации уменьшается погрешность энергии. Графики сигналов 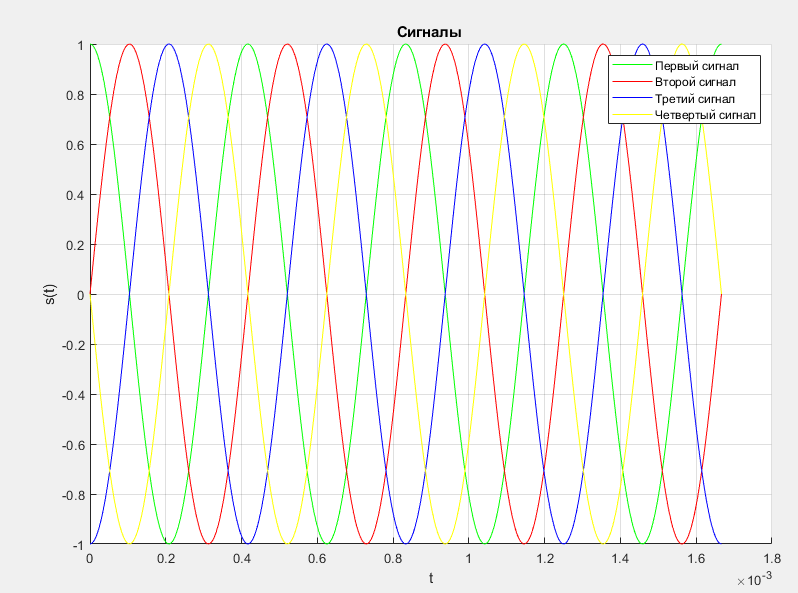 Рис. 1 Графики сигналов ФМ На данном графике видно 4 сигнала с значениями начальных фаз 0, 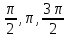 . .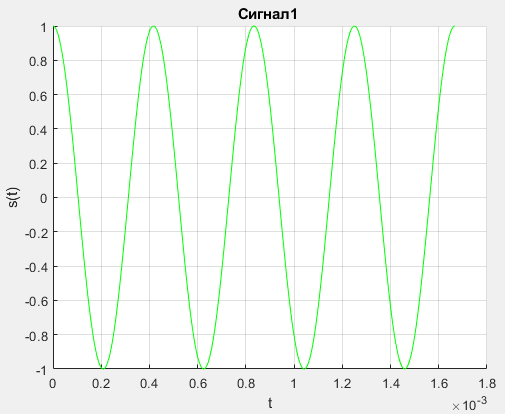 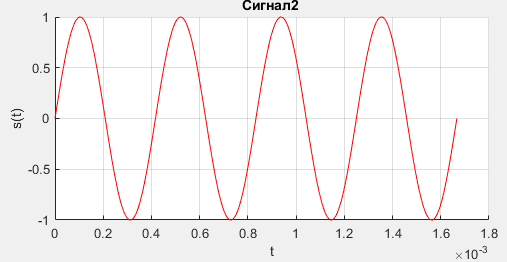 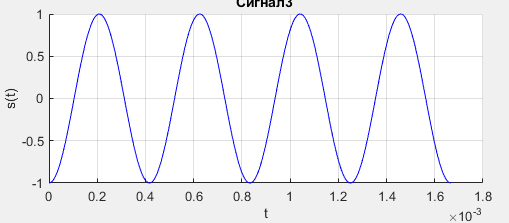 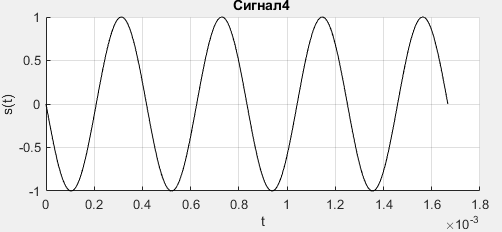 Рис. 2 Графики сигналов отличных по фазе Вывод: В данной лабораторной работе было определено количество сигналов в данном варианте q=4, фазовые сдвиги сигналов равные 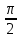 . Также были приведены аналитические выражения сигналов, подсчитана энергия каждого, которая равна 0,00083, и была произведена проверка значений, подсчитанных в среде Matlab, где была выявлена погрешности при дискретизации. Затем были построены графики сигналов, которые показаны на рис. 1. . Также были приведены аналитические выражения сигналов, подсчитана энергия каждого, которая равна 0,00083, и была произведена проверка значений, подсчитанных в среде Matlab, где была выявлена погрешности при дискретизации. Затем были построены графики сигналов, которые показаны на рис. 1.Код программы:
|
