Отчет по лабораторной работе «Изучение спектра атома водорода». Отчет по лабораторной работе Изучение спектра атома водорода
 Скачать 72.8 Kb. Скачать 72.8 Kb.
|
|
Отчет по лабораторной работе «Изучение спектра атома водорода» Цель работы: изучение видимой части спектра атомарного водорода и его анализ на основе квантовой теории Теоретическое введение Положение линий в атомных спектрах может быть объяснено только на основе квантовых представлений. Квантовая механика показывает, что энергия электронов в атоме может принимать не любые, а только некоторые определѐнные значения, образующие дискретный набор. Состояния с различными значениями энергии называются уровнями. Спектральные линии возникают при переходе электронов с одного уровня Em на другой (более низкий) En, энергия кванта равна разности энергий этих двух уровней:
где h – постоянная Планка. Совокупность линий, имеющих общий нижний уровень, составляет спектральную серию. Наиболее простую картину образуют уровни атома водорода (рис. 2). Теория показывает, что энергия уровней водорода рассчитывается по формуле:
где n – целое число (главное квантовое число); me – масса электрона; ε0 – электрическая постоянная; e – элементарный заряд. Из формул (1) и (2) следует, что частоты излучаемых квантов равны:
Так как частота и длина волны излучения связаны между собой ν = c / λ, то формулу (3) можно переписать в виде
где через R обозначена величина, называемая постоянной Ридберга:
На рисунке 1 стрелками обозначены переходы между уровнями, соответствующие спектральным линиям. Видно, что линии в спектре водорода можно расположить по сериям: для всех линий серии значение n остается постоянным, а m может принимать любые целые значения от m = n +1 до 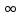 . .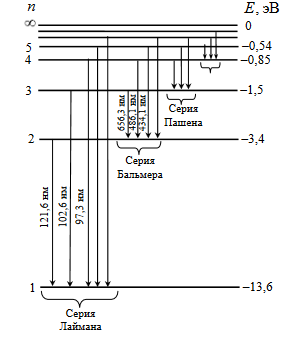 Рисунок 2 – Уровни энергии атома водорода и образование спектральных линий В настоящей работе изучается серия Бальмера, линии которой лежат в видимой области спектра. Для серии Бальмера n = 2 . Величина m для первых четырѐх линий этой серии принимает значения 3, 4, 5, 6. Эти линии обозначаются символами Нα, Нβ, Нγ, Нδ. В ходе работы нужно измерить длины волн этих линий, затем с помощью формулы (4) определить постоянную Ридберга и сравнить еѐ значение с расчѐтом по формуле (5). Установка содержит осветительное устройство ОУ с водородной и ртутной лампами, блок питания ламп БП и универсальный монохроматор УМ-2 (рис. 2). Водородная лампа представляет собой тонкую стеклянную трубку с двумя электродами, заполненную водородом под малым давлением. Вырабатываемое БП высокое напряжение прикладывается к электродам лампы и ускоряет в ней свободные электроны. Сталкиваясь с атомами и молекулами, они возбуждают их, вследствие чего возникает излучение фотонов. Аналогично работает ртутная лампа, только для еѐ свечения требуется более низкое напряжение (220 В). С помощью переключателя «ЛАМПА» на БП можно поочередно включать либо ртутную, либо водородную лампу. Для наблюдения и измерения спектров излучения используется высокоточный оптический прибор – универсальный монохроматор. Световой пучок от лампы собирается линзой L на входную щель 1, ширина которой может регулироваться микрометрическим винтом 2. С помощью коллиматорного объектива 3 пучок затем становится параллельным и попадает на сложную призму 5, склеенную из трѐх призм. В ней вследствие дисперсии лучи разных длин волн преломляются под различными углами. Призма, установленная на столике 6, может поворачиваться вокруг вертикальной оси с помощью микрометрического винта 7, снабжѐнного отсчѐтным барабаном. На нѐм нанесена винтовая канавка с градусными делениями. Вдоль канавки скользит указатель поворота барабана. При вращении барабана призма 5 поворачивается и в поле зрения наблюдателя попадают различные участки спектра. Объектив 8 в своей фокальной плоскости даѐт цветное изображение входной щели 1. Его рассматривают с помощью окуляра 9. В случае надобности окуляр можно вынести за пределы монохроматора, а на его место поставить выходную щель, которая пропустит одну из линий спектра. 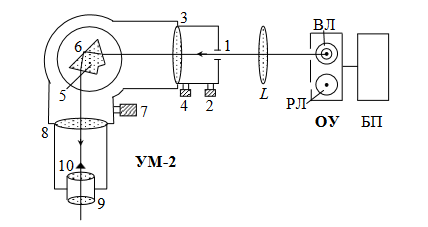 Рисунок 1 – Схема экспериментальной установки: ОУ – осветительное устройство: БП – блок питания ламп; ВЛ – водородная лампа; РЛ – ртутная лампа; L – линза УМ-2 – монохроматор: 1 – входная щель; 2, 4 – микрометрические винты; 3 – коллиматорный объектив; 5 – призма; 6 – поворотный столик; 7 – отсчѐтный барабан; 8 – объектив; 9 – окуляр; 10 – указатель Спектр, полученный с помощью призмы, является нелинейным, т.е. отсчѐт по шкале барабана не связан с длиной волны λ прямой пропорциональной зависимостью. Поэтому монохроматор нуждается в предварительной градуировке. С этой целью используется ртутная лампа ДРСк-125, так как длины волн спектра ртути хорошо известны. Если, наблюдая в монохроматор ртутный спектр, отметить отсчѐты на барабане, соответствующие длинам волн отдельных линий, то можно построить график зависимости отсчѐта N от длины волны λ. Этот график можно использовать в дальнейшем при изучении спектра водорода: с его помощью определять λ по величине отсчѐта N на барабане. Экспериментальная часть В таблице представлен набор данных, полученных при измерениях в лабораторной работе «Изучение спектра атома водорода». Таблица 1. Набор полученных и расчетных данных лабораторной работы
По результатам таблицы 1 был построен график зависимости λ от N, представленный на рисунке 3. 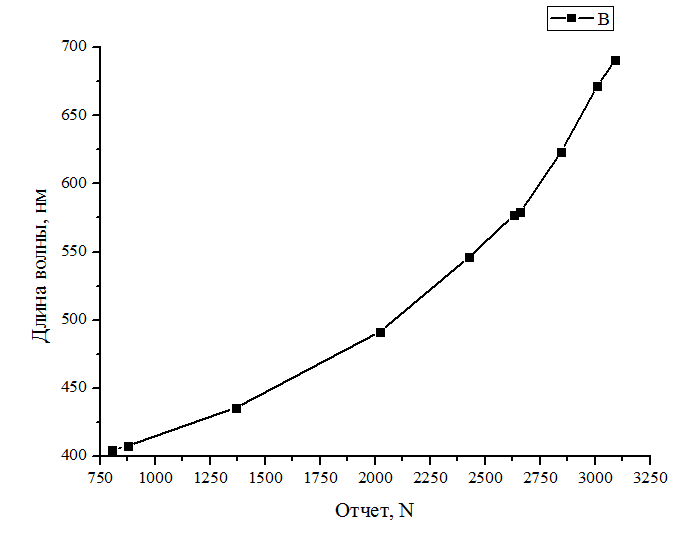 Рисунок 3 – График зависимость λ от N По графику зависимости λ от N определили длины волн для линий Нα, Нβ, Нγ водородной лампы. Результаты представлены в таблице 2. Таблица 2. Результаты расчетов длин волн для водородной лампы.
По результатам длин волн водородной лампы были посчитаны постоянные Ридберга. Результаты представлены в таблице 3. Таблица 3. Результаты расчетов постоянных Ридберга.
Пример расчетов: Среднее значение шкалы отсчета 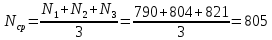 Расчет постоянной Ридберга: 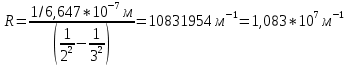 Выводы Мне были предоставлены данные указанные в таблице 1 и 2 для измерений, и по ним, пользуясь формулами указанных в экспериментальной части и формулой (4) был проведен расчет экспериментальных данных. Значение постоянной Ридберга составило 1,083; 1,112 и 1,095·107 м-1, что очень хорошо согласуется с табличными значениями 1,1·107 м-1 |

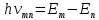 ,
,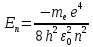 ,
,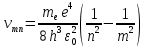 .
.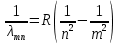 ,
,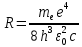 .
.