лр 3. Отчет по лабораторной работе по дисциплине
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ БОЛЬЦМАНА И ОПРЕДЕЛЕНИЕ РАБОТЫ ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА В ВАКУУМ Отчет по лабораторной работе по дисциплине «Физика»
Томск 2022 1. ЦЕЛЬ РАБОТЫ Целью настоящей работы является изучение распределения Больцмана на примере исследования температурной зависимости тока термоэлектронов, а также определение работы выхода электронов из металла в вакуум. 2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА 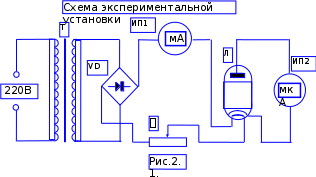 Схема экспериментальной установки приведена на рис.2.1. Первичная обмотка трансформатора Т питается от сети переменного тока напряжением 220 В. Вторичная обмотка подключена к диодному мосту VD, выпрямленное напряжение с которого подается на накальную спираль электронной лампы Л. Регулировка тока накала производится сопротивлением R, движок управления которым выведен на лицевую панель установки. На этой же панели расположен миллиамперметр ИП1. Определение температуры катода осуществляется по величине тока накала IН , измеренного миллиамперметром ИП1, с помощью градуировочной кривой. Для измерения тока IA термоэлектронов, попадающих на анод, служит микроамперметр ИП2, включенный в анодную цепь. Прибор ИП2 также расположен на лицевой панели установки. Суть эксперимента заключается в измерении зависимости анодного тока IA от тока накала IН . 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Работа выхода электрона из металла (в Дж): E = -ka, (3.1) где k - постоянная Больцмана; a - угловой коэффициент линеаризованного графика 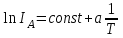 (3.2) (3.2)Абсолютная приборная погрешность вычисляется так: 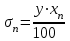 (3.3) (3.3)где у - класс точности применяемого прибора, хn – так называемое «нормирующее значение». Доверительный интервал равен =2( ln IA) где ln IA – величина, измеряемая косвенно, то результат этого измерения – это функция одного или нескольких прямых измерений, (где (ln IA)– абсолютные погрешности равные приборным абсолютным погрешностям). 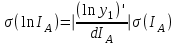 (3.4) (3.4)где (3.8) – формула для определения погрешности косвенного измерения прологарифмированного тока термоэлектронов. где у1– это функция одного или нескольких прямых измерений. 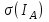 - абсолютные приборные погрешности. - абсолютные приборные погрешности.Доверительный интервал равен =2  1/Т 1/Тгде 1/Т – величина, измеряемая косвенно, то результат этого измерения – это функция одного или нескольких прямых измерений, следовательно абсолютная погрешность  1/Т равна: 1/Т равна: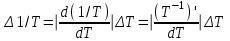 (3.5) (3.5)где (3.9) – формула для определения погрешности косвенного измерения обратной температуры. где 1/Т - косвенно измеряемая величина, 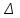 Т - абсолютная погрешность измеряемой величины, Т – прямо измеряемая величина. Т - абсолютная погрешность измеряемой величины, Т – прямо измеряемая величина.Где 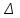 T =0,5К т.к. класс точности прибора не указан. В этом случае абсолютная погрешность п(Т) не зависит от результата измерения Т. И так как прибор – не цифровой, а- линейка, то п(Т) равна половине цены деления прибора. T =0,5К т.к. класс точности прибора не указан. В этом случае абсолютная погрешность п(Т) не зависит от результата измерения Т. И так как прибор – не цифровой, а- линейка, то п(Т) равна половине цены деления прибора.4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. Экспериментальные данные и результаты их обработки представлены в таблице. Результаты прямых и косвенных измерений таб. 4.1
Результаты измерений приведены в таблице 4.1. Там же представлены рассчитанные ln IA и 1/T. Абсолютные приборные погрешности по формуле (3.3) равны: 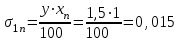 мА и мА и 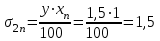 мкА. мкА.Доверительный интервал (учитывая косвенность измерений равен 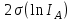 ) находим по формуле (3.4) ) находим по формуле (3.4)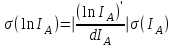 =1,5/9=0,17мкА =1,5/9=0,17мкА 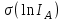 =1,5/13=0,115 мкА =1,5/13=0,115 мкА 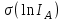 =1,5/18=0,083 мкА =1,5/18=0,083 мкА 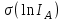 =1,5/25=0,06 мкА =1,5/25=0,06 мкА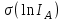 =1,5/33=0,045мкА =1,5/33=0,045мкА 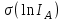 =1,5/45=0,033 мкА =1,5/45=0,033 мкА 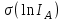 =1,5/59=0,0254 мкА =1,5/59=0,0254 мкА 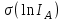 =1,5/77=0,019 мкА =1,5/77=0,019 мкА Доверительные интервалы ln IA: -11.61 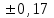 ; ; -11.25 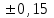 -10.92 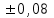 ; ;-10.59 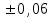 ; ;-10.31 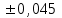 ; ;-10.00 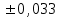 ; ;-9.737 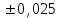 ; ;-9.47 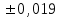 ; ;Абсолютные погрешности 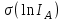 для других экспериментальных точек приведены в таб. 4.2 для других экспериментальных точек приведены в таб. 4.2таб. 4.2
По формуле (3.5) найдем абсолютную погрешность косвенно измеряемой ве личины – 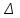 1/T. 1/T. 1) ( 1/T)1 = 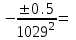 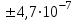 ; 5) ( 1/T)2 = ; 5) ( 1/T)2 = 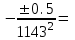 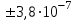 ; ;2) ( 1/T)3 = 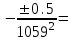 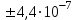 ; 6) ( 1/T)4 = ; 6) ( 1/T)4 = 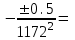 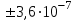 ; ;3) ( 1/T)5 = 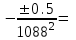 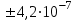 ; 7) ( 1/T)6 = ; 7) ( 1/T)6 = 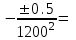 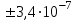 ; ;4) ( 1/T)7 = 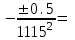 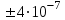 ; 8) ( 1/T)8 = ; 8) ( 1/T)8 = 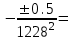 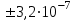 ; ;Доверительные интервалы 1/T: 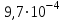 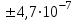 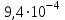 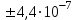 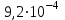 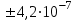 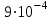 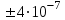 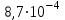 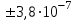 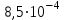 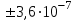 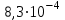 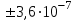 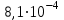 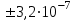 Абсолютные погрешности 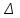 1/T для всех экспериментальных точек приведены в Таблице 4.3 1/T для всех экспериментальных точек приведены в Таблице 4.3таб. 4.3
График Зависимость ln I от 1/T. График идет ниже оси ОХ т.к. ln I брал от 9∙10-6, 13∙10-6, 18∙10-6, 25∙10-6, 33∙10-6, 45∙10-6, 59∙10-6, 77∙10-6 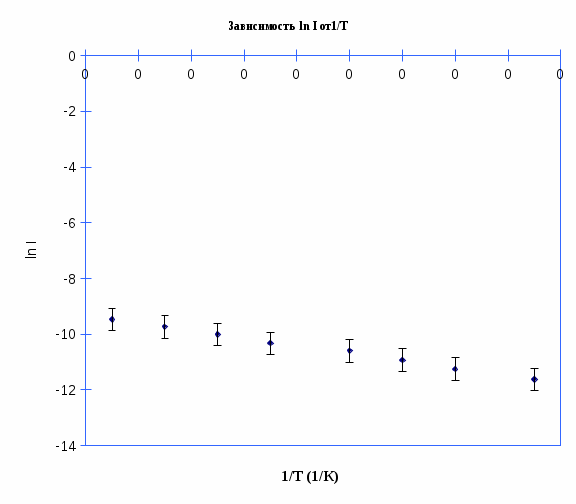 Далее рассчитаем угловой коэффициент графика по формуле (3.2): 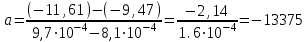 Из формулы 3.3 определил угловой коэффициент и он равен -13375следовательно работа выхода электронов(3.1) равна 1,380622∙10-23∙13375 и равна 1,8465∙10-19(Дж) ВЫВОДЫ. В результате проделанной лабораторной работы на экспериментальной установке мы провели исследования температурной зависимости тока термоэлектронов в системе металл-вакуум. На примере практического исследования температурной зависимости тока термоэлектронов убедились в справедливости закона распределения Больцмана. Произведя сравнение интерполирующей прямой с ее уравнением определили работу выхода электронов из металла в вакуум. С целью изучения распределения Больцмана была исследована температурная зависимость тока термоэлектронов, имеется линейная зависимости. Определена работу выхода электронов из металла. Линейность графика подтверждает закон распределения Больцмана, который гласит: «концентрация частиц газа зависит от их потенциальной энергии во внешнем поле». Работа выхода равна электрона из металла равна 1,8465∙10-19(Дж) Ответы на контрольные вопросы: 1. Под распределением Больцмана понимают зависимость концентрации частиц газа от их потенциальной энергии во внешнем поле: 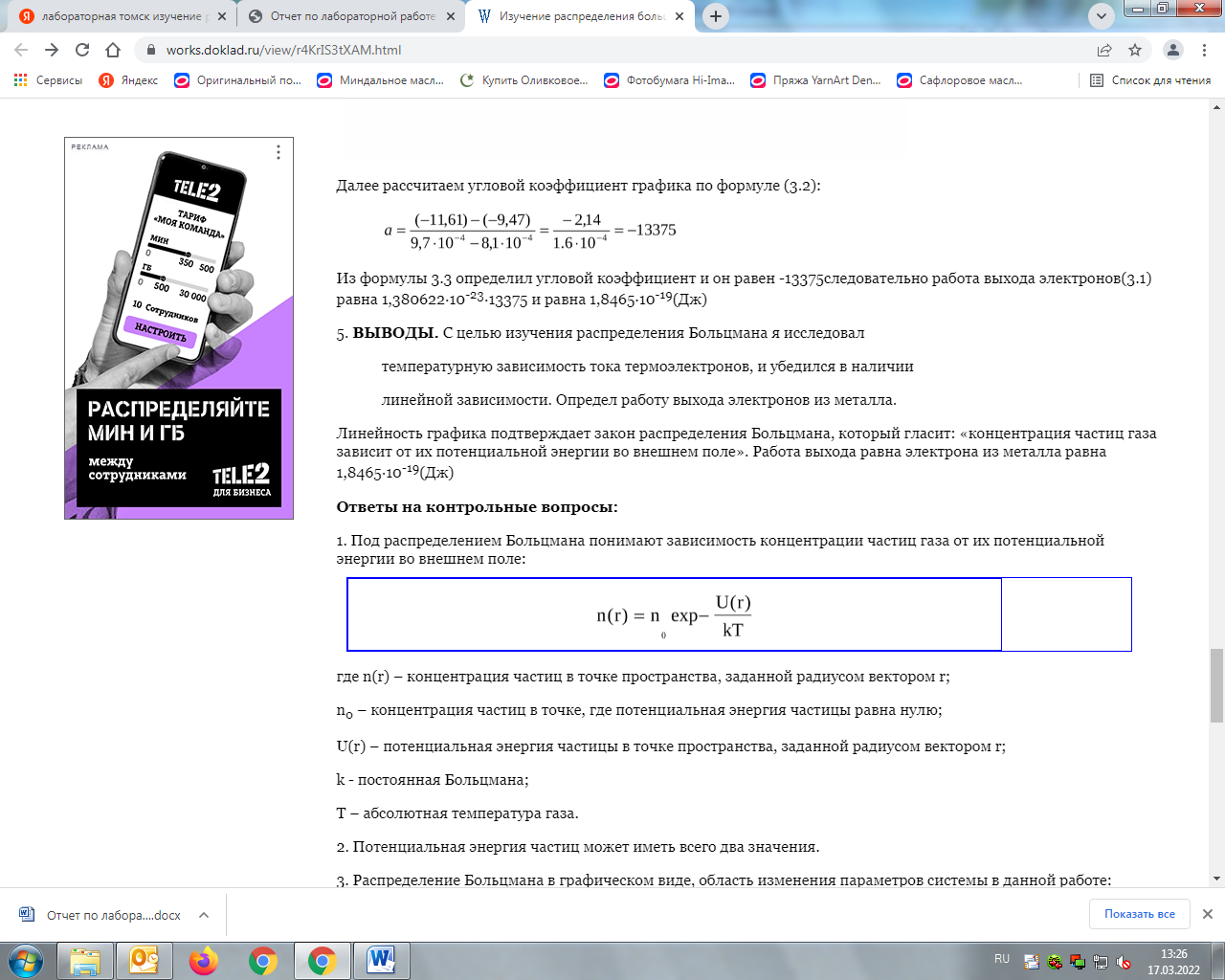 где n(r) – концентрация частиц в точке пространства, заданной радиусом вектором r; n0 – концентрация частиц в точке, где потенциальная энергия частицы равна нулю; U(r) – потенциальная энергия частицы в точке пространства, заданной радиусом вектором r; k - постоянная Больцмана; T – абсолютная температура газа. 2. Потенциальная энергия частиц может иметь всего два значения. 3. Распределение Больцмана в графическом виде, область изменения параметров системы в данной работе: 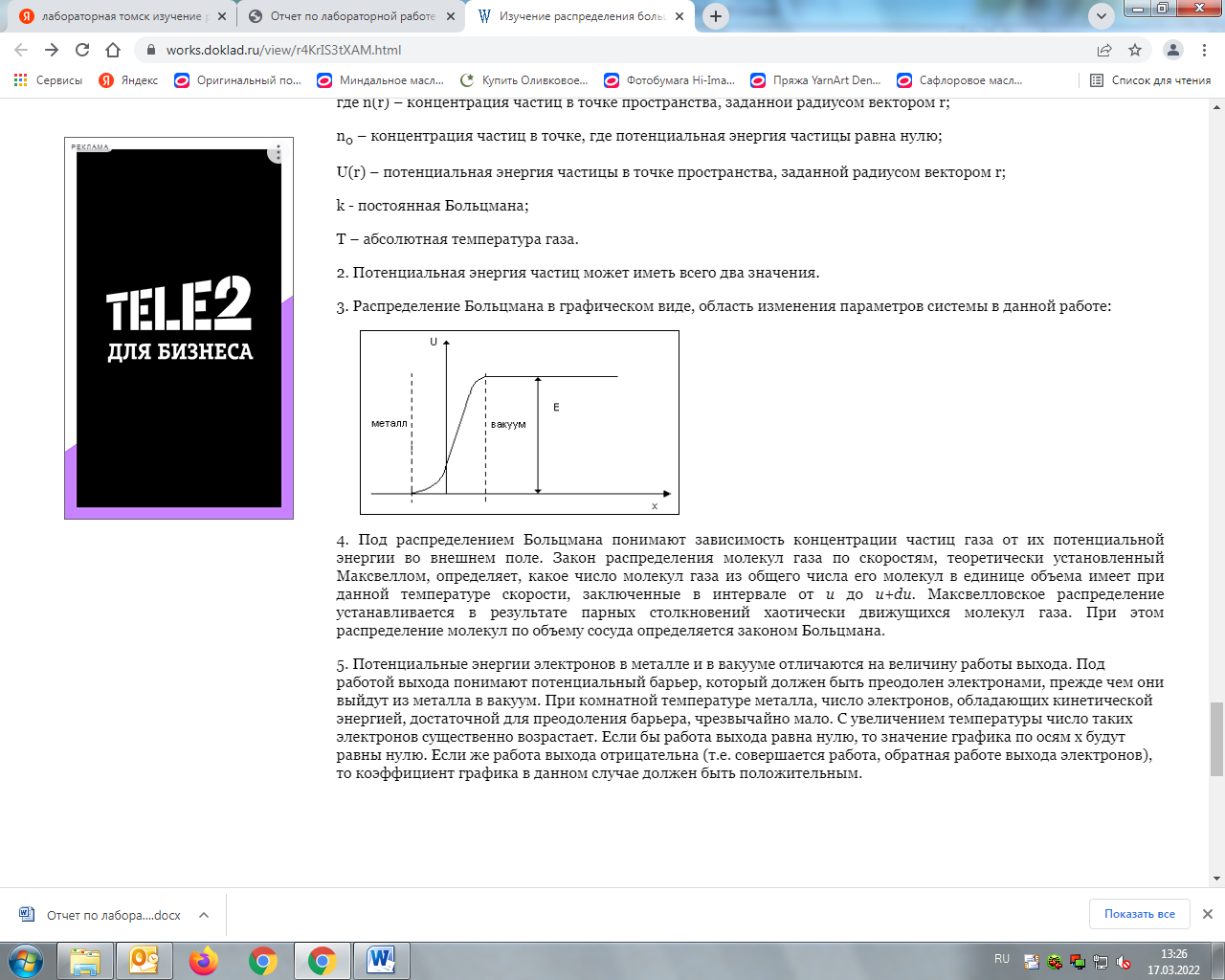 4. Под распределением Больцмана понимают зависимость концентрации частиц газа от их потенциальной энергии во внешнем поле. Закон распределения молекул газа по скоростям, теоретически установленный Максвеллом, определяет, какое число молекул газа из общего числа его молекул в единице объема имеет при данной температуре скорости, заключенные в интервале от u до u+du. Максвелловское распределение устанавливается в результате парных столкновений хаотически движущихся молекул газа. При этом распределение молекул по объему сосуда определяется законом Больцмана. 5. Потенциальные энергии электронов в металле и в вакууме отличаются на величину работы выхода. Под работой выхода понимают потенциальный барьер, который должен быть преодолен электронами, прежде чем они выйдут из металла в вакуум. При комнатной температуре металла, число электронов, обладающих кинетической энергией, достаточной для преодоления барьера, чрезвычайно мало. С увеличением температуры число таких электронов существенно возрастает. Если бы работа выхода равна нулю, то значение графика по осям x будут равны нулю. Если же работа выхода отрицательна (т.е. совершается работа, обратная работе выхода электронов), то коэффициент графика в данном случае должен быть положительным. Что называется распределением Больцмана? Распределение Больцмана – это зависимость концентрации частиц газа от их потенциальной энергии во внешнем поле. Сколько значений потенциальной энергии частиц реализуется в экспериментальной установке, применяемой в данной работе? В данной работе потенциальная энергия частиц имеет два значения. Представить распределения Больцмана графически и указать на графике область изменения параметров системы в данной работе.  Кривая, описывающая распределение Больцмана по потенциальной энергии Что общего и в чём различия распределений Больцмана и Максвелла?
Какова физическая причина существования работы выхода электронов из металла? Что было бы, если бы работа выхода равнялась нулю и была отрицательной? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
