лаба. Отчет по лабораторной работе по физике студент Группа
 Скачать 0.61 Mb.
|
|
Алтайский государственный технический университет им. И.И. Ползунова Кафедра физики ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ
Барнаул - 2019ВВЕДЕНИЕ. РАСЧЕТ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ В своей жизни человеку постоянно приходится проводить измерения, будь то научные исследования, проектирование, строительство или простая покупка товара в магазине. Под измерением понимают сравнение измеряемой величины с ее известным значением, называемым эталоном. При этом за значение X измеряемой величины принимают число, показывающее, сколько раз в измеряемой величине содержится эталон. Следует помнить, что никакое измерение не может быть выполнено абсолютно точно. Его результат обязательно содержит некоторую погрешность. Каждое измерительное устройство обязательно содержит некоторую погрешность изготовления тех или иных измерительных шкал. Измеряя с помощью такого инструмента некоторую величину, мы не можем сделать ошибки меньшей, чем погрешность измерительного устройства. Кроме того, в процессе измерений возникают и случайные ошибки, связанные с повторяемостью физических измерений. Измерения делятся на прямые и косвенные. Прямые измерения производятся с помощью приборов, которые непосредственно измеряют саму физическую величину. Так, массу тела можно измерить с помощью весов, длину с помощью линейки и т.д. Если физическую величину невозможно измерить с помощью приборов, то ее конечный результат находится по формуле через величины, определяемые в результате прямых измерений. Такой метод измерения называется косвенным. 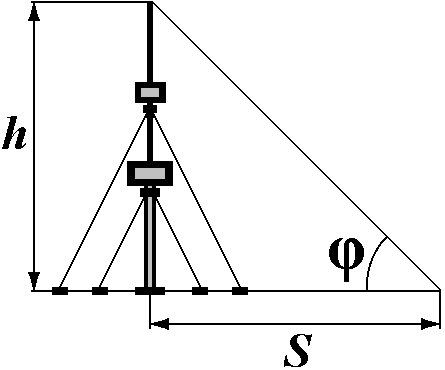 Рис. 1. Определение высоты башни. Предположим, к примеру, что нужно измерить высоту h телевизионной башни. Можно взять мерную ленту достаточно большой длины, забраться на вершину башни закрепить там конец ленты, а затем спуститься и прочитать отсчет у поверхности Земли, который соответствует высоте телебашни. Это как раз случай прямых измерений – измеряемая величина (высота) считывается по прибору (мерной ленте). Однако выполнять такие действия крайне опасно. Гораздо проще (рис. 1) поставить угломерный прибор, например, теодолит, на известном расстоянии S от башни и измерить угол , опирающийся на вершину и основание башни. Тогда высота будет определяться по формуле  . Результат косвенного измерения всегда рассчитывается по формуле на основании прямых измерений.Точность измерений характеризуется их погрешностью. Абсолютной погрешностью измерения Х называют модуль разности между измеренным значением Х и ее истинным значением   . (1)Истинное значение  , вообще говоря, остается неизвестным. Однако с определенной вероятностью можно сказать, что оно находится в интервале . (2)В зависимости от свойств и причин возникновения различают три основных типа погрешностей (ошибок): систематические, случайные погрешности и промахи. Систематическая погрешность измерения обусловлена прибором, которым проводится измерение. Невозможно идеально изготовить прибор. Например, длина линейки в действительности может отличаться от того значения, которое написано на ней. Два последовательно включенных амперметра могут показывать различный ток и т.д. Приборы, тем не менее, считаются исправными, если их показания отличаются от истинного значения не более чем на величину абсолютной систематической погрешности измерения. Отклонение показаний прибора происходит всегда в одну и ту же сторону. Однако исследователю, как правило, неизвестно, в какую именно сторону происходит отклонение. Абсолютная систематическая погрешность измерения определяется тремя способами: по классу точности прибора; на приборе, как число с наименованием единиц величин, измеряемых прибором; как половина цены наименьшего деления шкалы прибора. Остановимся подробно на каждом из них. Определение абсолютной систематической ошибки по классу точности прибора. Этот способ используется только для электроизмерительных приборов, например, для вольтметра, амперметра. Класс точности  прибора, предназначенного для измерения физической величины Х, определяется следующим образом , (3)где  наибольшее предельное значение величины Х, которое можно измерить данным прибором. Если известен класс точности прибора, то из соотношения (3) можно выразить абсолютную систематическую погрешность измерения . (4)Например, класс точности амперметра равен 1,5, а наибольший ток, который можно измерить этим амперметром при конкретном положении его ручек настройки составляет 5 А. Тогда систематическая погрешность окажется равной  .Причем это значение не зависит от результатов измерений. Из формулы (4) видно, что систематическая погрешность тем меньше, чем меньше класс точности прибора. Класс точности прибора обозначается на приборе как число в десятичном формате (может быть обведено в кружок). Стандартом установлены семь классов точности приборов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Приборы классов 1,0; 1,5; 2,5; 4,0 применяют для технических целей и называют техническими. Приборы классов 0,1; 0,2; 0,5 применяют для точных лабораторных измерений, а также для контроля технических. Их называют прецизионными. 2. Определение абсолютной систематической ошибки как числа с наименованием единиц величин, измеряемых прибором, используется для точных измерительных приборов, например, для штангенциркуля, микрометра. В этом случае абсолютная систематическая погрешность указывается непосредственно на самом приборе как число с наименованием. Например, 0,1 мм на штангенциркуле, 5 г на весах. 3. Определение абсолютной систематической ошибки как половины цены наименьшего деления шкалы прибора используется для простых измерительных приборов, например для линейки. Так, при измерении линейкой с делением шкалы 1 мм абсолютная систематическая погрешность будет равна 0,5 мм. Точность прибора невозможно превзойти никаким методом измерения на нем. Кроме абсолютной систематической погрешности существует абсолютная случайная погрешность ∆Хсл. Случайная погрешность обусловлена случайными факторами, которые, в свою очередь, могут быть вызваны различными причинами. С одной стороны это могут быть причины, не зависящие от измеряемой величины, например, состояние организма человека, наблюдающего за прибором, погодные и природные условия, состояние рабочего места и др. С другой - сама измеряемая величина может носить случайный характер. Например, количество транспортных средств на участке дороги, температура и влажность воздуха в различных частях города, концентрация примесей в различных пробах воды и т.п. В любом случае за истинное значение величины Х принимают ее среднее значение Хср. Для этого проводят несколько измерений Х1, Х2, ... Хn и рассчитывают Хср  , (5)где n число измерений. Очевидно, что чем больше измеренные значения отличаются друг от друга, тем больший разброс имеет величина Х. Для того, чтобы оценить величину этого разброса, разработан специальный математический аппарат. Мы познакомимся только с результатами этих расчетов. Прежде всего, вычисляется стандартный доверительный интервал (среднее квадратичное отклонение) 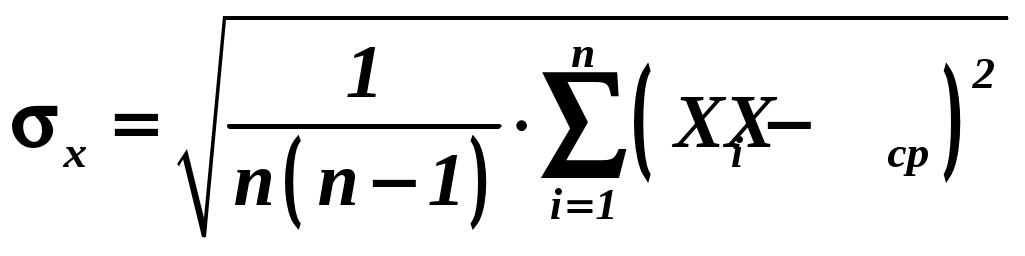 . (6)В знаменателе под корнем не может стоять n, т.к. стандартный интервал Х возрастал бы при увеличении числа измерений, что неестественно. Не может там быть и n2, т.к. при одном единственном измерении величина оказалась бы нулевой, что также неестественно. Можно ли считать, что величина случайной погрешности равна стандартному доверительному интервалу? Нет, нельзя. Для того чтобы определить величину случайной погрешности Хсл, необходимо определить так называемую доверительную вероятность (надежность) . Это вероятность того, что значение измеренной величины окажется в интервале от ХХ до ХХ. Например, после ста контрольных измерений диаметра стандартной двадцатимиллиметровой трубы обнаружено, что в 50 случаях ее диаметр оказался в интервале от 19,97 мм до 20,03 мм, в 80 случаях от 19,95 до 20,05 мм, а в 95 случаях от 19,90 до 20,10 мм. Следовательно, можно приближенно оценить величину случайной погрешности. При надежности =0,50, Хсл=0,03 мм; при надежности =0,80, Хсл=0,05 мм; а при =0,95, Хсл =0,10 мм. То есть, величина случайной погрешности увеличивается с увеличением надежности, причем очень резко при стремлении к единице. Действительно, с надежностью, равной 1, ничего нельзя гарантировать. При построении техники всегда задается определенная надежность изделия. Каждая деталь должна соответствовать надежности не ниже той, которая предъявляется ко всему изделию в целом. Если техника достаточно сложная, то отклонение параметров деталей от заданных значений должно быть очень малым. Уменьшение отклонения Х при одновременном увеличении чрезвычайно трудная задача. Например, при изготовлении кастрюль можно задать =0,98 и отклонение от стандартных размеров в пределах 2%. А при изготовлении самолета необходимо положить 0,9999, и относительное отклонение от стандарта не более 0,001%. В этом состоит одна из причин того, что стоимость десятитонного самолета во много раз превышает стоимость 10 тонн алюминиевых кастрюль. При увеличении числа измерений величина случайной погрешности уменьшается. Однако при большом числе измерений это уменьшение оказывается крайне незначительным. Для того, чтобы учесть зависимость Хсл от и n, вводится специальный коэффициент tn, , называемый коэффициентом Стьюдента. Случайная погрешность определяется следующим выражением:  . (7)Коэффициент Стьюдента можно определить по специальной таблице (см. таблицу 2). При лабораторных измерениях обычно полагают =0,95 и ограничиваются 3-4 измерениями. При =0,95 t3;0,95 = 4,3; t4;0,95 =3,2. Промахи (или грубые погрешности) проявляются обычно в резком отклонении результата отдельного измерения от остальных. Промахи обусловлены главным образом недостаточным вниманием экспериментатора или неисправностями средств измерения. Промахи устраняют повторным более внимательным измерением или отбрасывают результаты как ошибочные. Полная абсолютная погрешность Х при прямых измерениях находится путем сложения случайной и систематической погрешностей:  . (8)Погрешность при косвенных измерениях находится двумя способами: как полный дифференциал с последующей заменой дифференциалов соответствующими погрешностями; путем логарифмирования и последующего дифференцирования расчетной формулы. Рассмотрим подробнее каждый из способов нахождения погрешности косвенных измерений. 1. Определение погрешности косвенных измерений как полный дифференциал с последующей заменой дифференциалов соответствующими погрешностями. Если искомая величина является функцией нескольких переменных, например, f(x,y), то погрешность косвенных измерений можно определить по формуле:  . (9)Например, ускорение при поступательном движении определяется как  .Тогда  ,  .Так как  , то  Независимо от знака производных, слагаемые в последнем выражении должны учитываться только со знаком «+», так как погрешность при измерении нескольких переменных может только увеличиваться. Если в формулу входят константы, то при расчетах в них необходимо учитывать хотя бы на одну значащую цифру больше, чем в измеряемой величине, тогда они практически не вносят погрешности в результат измерения. 2. Определение погрешности косвенных измерений путем логарифмирования и последующего дифференцирования расчетной формулы. Например, абсолютная погрешность в определении ускорения может быть найдена в результате логарифмирования и последующего дифференцирования соотношения .Логарифмируем расчетную формулу: ln а = ln 2 + lnh – lnt2. Дифференцируем полученное выражение:  .Заменяя дифференциалы на соответствующие им абсолютные погрешности величин прямых измерений, и учитывая, что независимо от знака дифференциалов, слагаемые берутся только со знаком «+», так как погрешность при измерении нескольких переменных может только увеличиваться, получим:  ,  .Абсолютная погрешность измерения представляет собой необходимую информацию об измеряемой величине. Однако, она не всегда оказывается наглядной. Допустим, что X=5 см. Много это или мало? Если измеряется длина подошвы Х, то это много. Если Х это длина комнаты, то это немного. Если же Х расстояние между автобусными остановками, то это ничтожно мало. Иначе воспринимается так называемая относительная погрешность 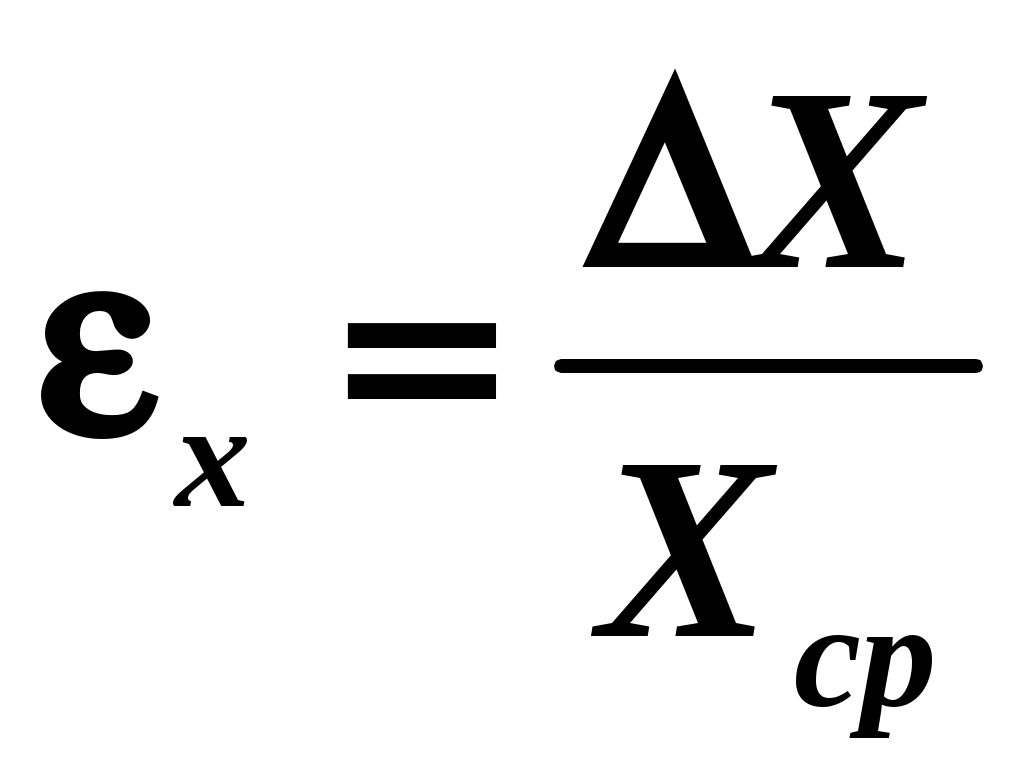 , (10)которую можно выразить в процентах, если умножить на 100 %. Окончательный результат измерения представляется в виде:  < единицы измерения >; ε = … % ; = < значение >. (11)Например, а=(2,9 0,3) м/с2 ; = 10,3 % ; =0,95. Правильная запись окончательного результата предполагает его округление. Для этого нужно вспомнить, что такое значащие цифры (знаки) в числе. Любое число можно представить с произвольным количеством нулей слева. Например, 00052,0310 = 52,031. Первая ненулевая цифра слева это первая значащая цифра. В данном случае это цифра 5. Вторая цифра 2, третья 0 и т.д. Цифры справа от первой значащей формально также могут быть значащими, однако, в зависимости от измеряемой величины и способа ее измерения количество их также ограничено. Предположим, что среднее значение величины Х и ее абсолютная погрешность Х найдены. Перед округлением величин Хср и Х они должны быть приведены к одинаковым наименованиям. Множители типа 10n также должны быть одинаковыми. Например, значения X = 154,51010-2 м и Х = 3,814102 мм могут быть приведены к виду Х = 154,51 см, Х = 38,14 см. В первую очередь округляют погрешность Х. Так как Х это уже сама по себе погрешность, и, следовательно, определяет интервал допустимых значений, то указание ее с большой точностью (с большим количеством знаков после запятой) теряет смысл. В случае округления с точностью до десятых при округлении Х пользуются следующим правилом: если первая значащая цифра после запятой равна 1, то Х округляется до двух знаков (четвертая строка в таблице 1), в остальных случаях до одного знака. В тех случаях, когда измерения выполняются с большой точностью, округление результатов проводится с точностью, не меньшей точности прибора. Примеры округления результатов вычислений, в зависимости от заданной точности, приведены в таблице 1. Во всех случаях после округления количество знаков после запятой в погрешности Х и среднем значении величины Х должно быть одинаковым. Таблица 1. Правила округления результатов
Таблица 2. Значения коэффициентов Стьюдента
ЛАБОРАТОРНАЯ РАБОТА № 24. ( 2 часа ) ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТИКОМ УИТСТОНА Цель работы: ознакомиться с принципом работы схемы мостика Уитстона. Определить неизвестное сопротивление и удельное сопротивление проводника. 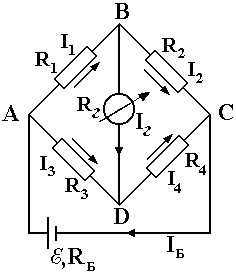 Рис. 2. Схема мостика Уитстона 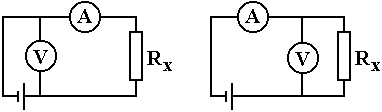 а) б) Рис. 1. Схема определения сопротивления Теоретическое введение. Наиболее часто для измерения сопротивления проводника применяется одна из схем, приведенных на рис. 1 (а и б), в силу их простоты. Однако любая из этих схем обладает существенным недостатком. В самом деле, любой прибор обладает конечным, но не нулевым сопротивлением. Поэтому, даже при высоком классе точности приборов, вольтметр, в первом случае, будет показывать суммарное падение напряжения на амперметре и исследуемом сопротивлении (показания амперметра соответствуют току через RХ). Во втором случае амперметр будет показывать суммарный ток, протекающий через вольтметр и сопротивление RХ. Показания же вольтметра соответствуют падению напряжения на RХ. Таким образом, в любом из этих случаев значение сопротивления RХ, найденное из закона Ома, будет неверным. а) б) Рис. 1. Схема определения сопротивления. Рис. 2. Схема мостика Уитсона. Схема, сводящая к минимуму влияние прибора на точность измерений, была предложена Уитстоном - так называемый мостик Уитстона (рис. 2). Четыре сопротивления R1,R2,R3,R4 образуют плечи мостика. RБ и - сопротивление и ЭДС батареи. Rг и Iг - сопротивление гальванометра и ток, протекающий через него. Для расчета сложных цепей, одной из которых является мостик Уитстона, применимы правила Кирхгофа. Первое правило: алгебраическая сумма токов, сходящихся в любой точке разветвленной цепи, равна нулю:  (1).Токи учитываются со знаком «+», если они приходят в рассматриваемую точку, и со знаком «–», если они выходят из этой точки. Первое правило Кирхгофа применяется к узловым точкам цепи, в которых сходятся три и более токов. Первое правило вытекает из закона сохранения электрического заряда. Второе правило: если несколько участков электрической цепи образуют замкнутый контур, то сумма падений напряжений на всех участках этого контура равна сумме ЭДС, действующих в этом контуре:  (2).Падение напряжения IR считается положительным, если выбранное направление тока на данном участке контура совпадает с направлением обхода контура и отрицательным, если направление тока и обхода противоположны. ЭДС имеет положительное значение, если при обходе контура внутри элемента переходим от «–» полюса источника к «+», и отрицательное, если наоборот. Воспользовавшись правилами Кирхгофа, можно получить шесть независимых уравнений для мостика Уитстона. По первому правилу Кирхгофа для узлов А, В и С: 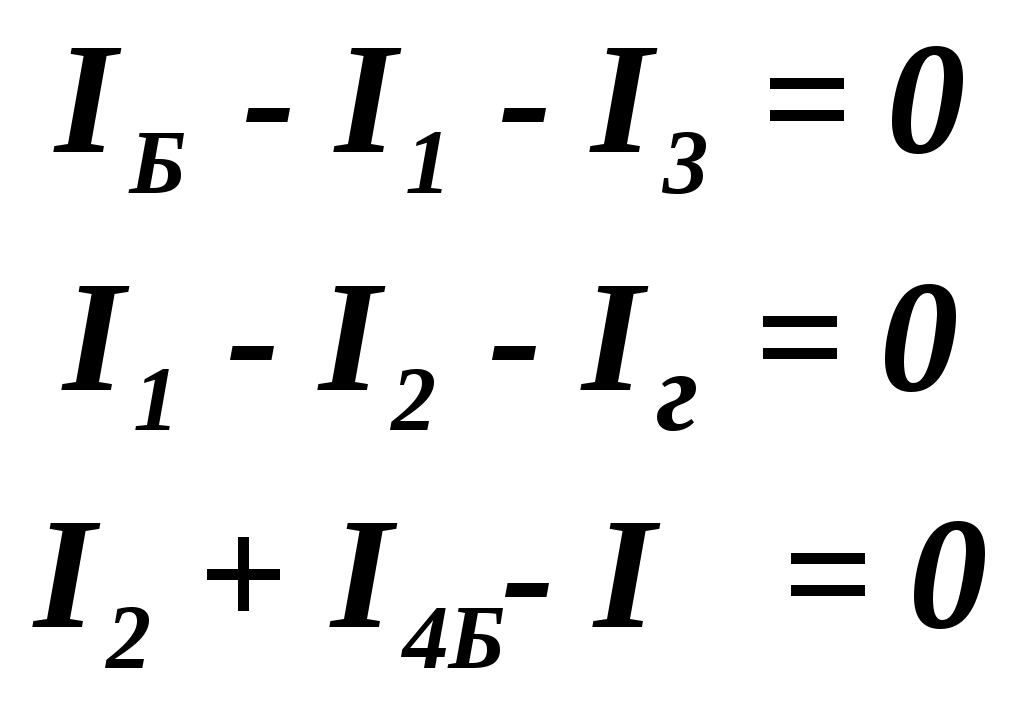 (3)По второму правилу Кирхгофа для контуров АВСА, АВDА и ВСDВ 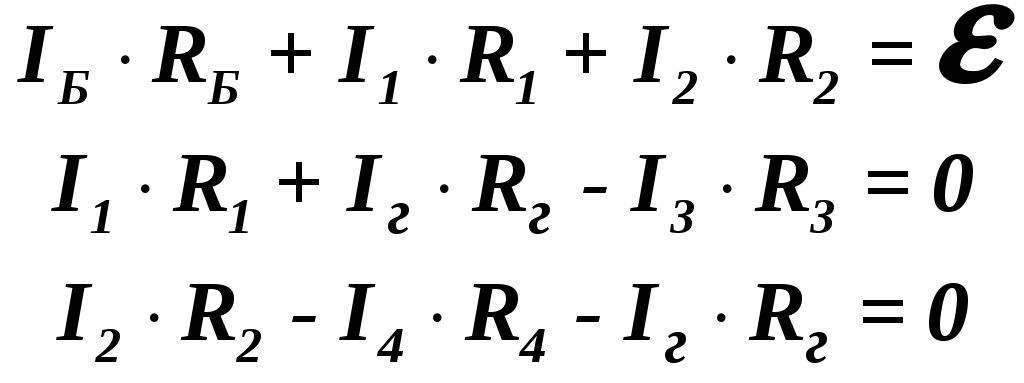 (4) .Эти уравнения позволяют найти шесть неизвестных величин. Если неизвестно одно из сопротивлений, например R1, то измеряя гальванометром силу тока Iг, из уравнений получают остальные токи и искомое сопротивление R1. Так поступают в случае неравновесного мостика Уитстона. Изменяя сопротивления R2,R3,R4, можно добиться, что ток через гальванометр станет равным нулю. В этом случае гальванометр не внесет искажений в схему, и уравнения (3) примут вид I1 = I2I3 = I4 , из уравнений (4) получим: I1R1 = I3R3 I2R2 = I4R4 , отсюда:  (5) .Неизвестное сопротивление R1 можно выразить через три других сопротивления  (6) .Равенство нулю силы тока через гальванометр определяет равновесное состояние мостика Уитстона. В этом случае, как видно из формулы (6), для вычисления неизвестного сопротивления необходимо знать абсолютное значение сопротивления R2 и отношение R3/R4. ОПИСАНИЕ УСТАНОВКИ 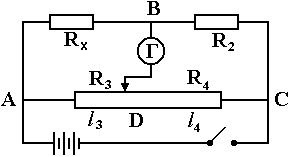 Рис. 3. Схема экспериментальной установки Для измерений применяется схема (рис. 3), аналогичная приведенной на рис. 2. В качестве сопротивления R2 используется магазин сопротивлений. Сопротивления R3 и R4 - участки реохорда - калиброванной проволоки, натянутой на деревянную линейку. Точка D представляет собой подвижный контакт - щуп. Передвигая щуп вдоль реохорда, уравновешивают схему, то есть добиваются положения, когда сила тока через гальванометр равна нулю. Так как реохорд изготовлен из однородной проволоки постоянного сечения, то сопротивления R3 и R4 оказываются пропорциональными длинам участков АD и DС. В этом случае отношение R3/R4 можно заменить отношением длин l3/l4. Неизвестное сопротивление найдется по формуле  (7) .Удельное сопротивление проводника находится из соотношения  (8) ,где l – длина проводника,S– площадь поперечного сечения;  ,  – средний диаметр проводники.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ЗАДАНИЯ На магазине сопротивлений R2 установить сопротивление 1 Ом. Положения остальных ручек должны соответствовать нулевым сопротивлениям. Уравновесить схему. Для этого щупом найти положение точки D, соответствующее нулевой силе тока через гальванометр, и определить длины l3 и l4. Данные R2, l3 и l4 занести в таблицу. Последовательно изменяя сопротивление R2 от 1 до 9 Ом, повторить пункт 2. Таблица 1
Вычислить в каждом из случаев сопротивление RХ по формуле (7). Рассчитать среднее значение RХ ср как среднее арифметическое всех  . Длину проводника принять равной 115см.Используя значение RХ ср , по формуле (8) найти удельное сопротивление проводника. Результаты занести в таблицу 1. Вычислить абсолютную и относительную погрешность измерений сопротивления RХпо результатам одной из средних строк таблицы, считая ошибки в определении длин l3 и l4 систематическими и равными 0,5 мм (l3=l4 =0,5 мм).  . По результатам работы сделать вывод.КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ В чем преимущество мостика Уитстона по сравнению со схемами, приведенными на рис. 1? Сформулировать и записать I и II правила Кирхгофа.
ОТЧЕТ
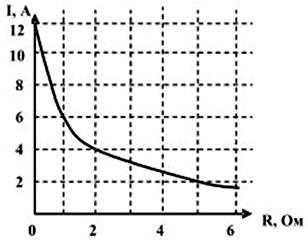
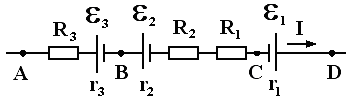
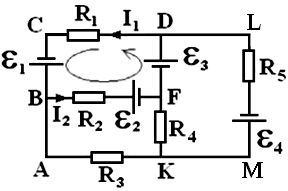
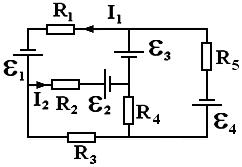
ЛАБОРАТОРНАЯ РАБОТА № 26. ( 2 часа ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В, 
В, R1=4 Ом, R2=6 Ом, R3=3 Ом, I1=3 А, I2=2 А. Величина Э.Д.С. источника тока 
равна …