Отчет по лабораторной работе свойства потоков вызовов

• Название: Отчет по лабораторной работе свойства потоков вызовов
• Дата: 07.12.2021
• Размер: 0.54 Mb.
• Имя файла: LR2_Konyukhov.docx
• Тип: Отчет; #295119

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана»
(МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	«Информатики и систем управления»
КАФЕДРА	«Защиты информации» (ИУ10)

ОТЧЕТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ

Свойства потоков вызовов.

Характеристики потоков.

Простейший поток вызовов.

ПО ДИСЦИПЛИНЕ:

«Моделирование трафика в защищенных сетях»

Студент ИУ10-91 М.В. Конюхов

(Группа) (Подпись, дата) (И.О. Фамилия)
Проверила В.М.Антонова

(Подпись, дата) (И.О. Фамилия)

2021  г.

Оглавление

1.Теоретическая часть 2

2.Практическая часть 5

Вывод 8

1. Теоретическая часть

Поток вызовов – это дискретный процесс, последовательность однородных событий, которые наступают через некоторые интервалы времени при непрерывном отсчете времени.

Случайный поток – это поток, в котором однородные события наступают через случайные интервалы времени.

Свойства потоков: стационарность, ординарность и полное или частичное отсутствие последействия. Потоки классифицируются с точки зрения наличия или отсутствия этих свойств.

Случайный поток может быть задан тремя эквивалентными способами:

1.Функцией распределения вызывающих моментов P(t<t_i), где t– случайная величина, t_i– возможное значение случайной величины.

2.Функцией распределения промежутков между вызывающими моментами P(z<z_i), где z_i= t_i- t_i-1при i≥1.

3.Законом распределения целочисленной функции K(t),т.е. P_k(t)=P[K(t)=k_i],i=1, 2, …, n , k₁ ≤ k₂ ≤ … ≤ k_n, t₁< t₂ <…< t_n .

P_k(t)=P[K(t)= k_i] – вероятность поступления k_iвызовов в интервале времени [0,t).

Для задания случайных потоков используется вероятность поступления не менее kвызовов на интервале времени [0,t) P_i≥k(t).

Потоки характеризуются тремя свойствами: стационарность, ординарность, последействие или его отсутствие.

Основными характеристиками потоков вызовов являются интенсивность μ(t) и параметр λ(t)

Стационарный, ординарный поток без последействия называется простейшим.

Для простейшего потока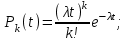



F(t) = P(Z < t) = 1 – e^–λt,

где 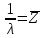- математическое ожидание промежутка времени между двумя последовательными моментами поступления вызовов.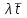

– интенсивность поступающей телефонной нагрузки.

;

;

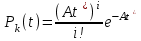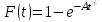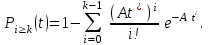2. Практическая часть

Исходные данные: (Вариант 11)

А1 = 0.45

А2 = 0.93

V = 11

Функция распределения вызывающих моментов

P_k(t^*), где t^*=0,5;1,0;1,5;2,0

Посчитаем распределение, используя формулу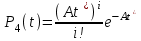



Код программы на Python для вычисления формулы:

import math
A1 = 0.45

i = 0

print("A1=0.45:")

for t in (0.5, 1.0, 1.5, 2.0):

i += 1

P = round(((((A1 * t) ** i) / (math.factorial(i) * math.exp(A1 * t)))), 4)
print('P' + str(i) + "(" + str(t) + ") = " + str(P))
A2 = 0.93

i = 0

print("A2=0.93:")

for t in (0.5, 1.0, 1.5, 2.0):

i += 1

P = round(((((A2 * t) ** i) / (math.factorial(i) * math.exp(A2 * t)))), 6)

print('P' + str(i) + "(" + str(t) + ") = " + str(P))

Результаты вычислений запишем в таблицу.

t*	0,5	1,0	1,5	2,0
Рк(t*,А1)	0.1797	0.0646	0.0261	0.0111
Рк(t*,А2)	0.2920	0.1706	0.1121	0.0776

Построим по полученным результатам график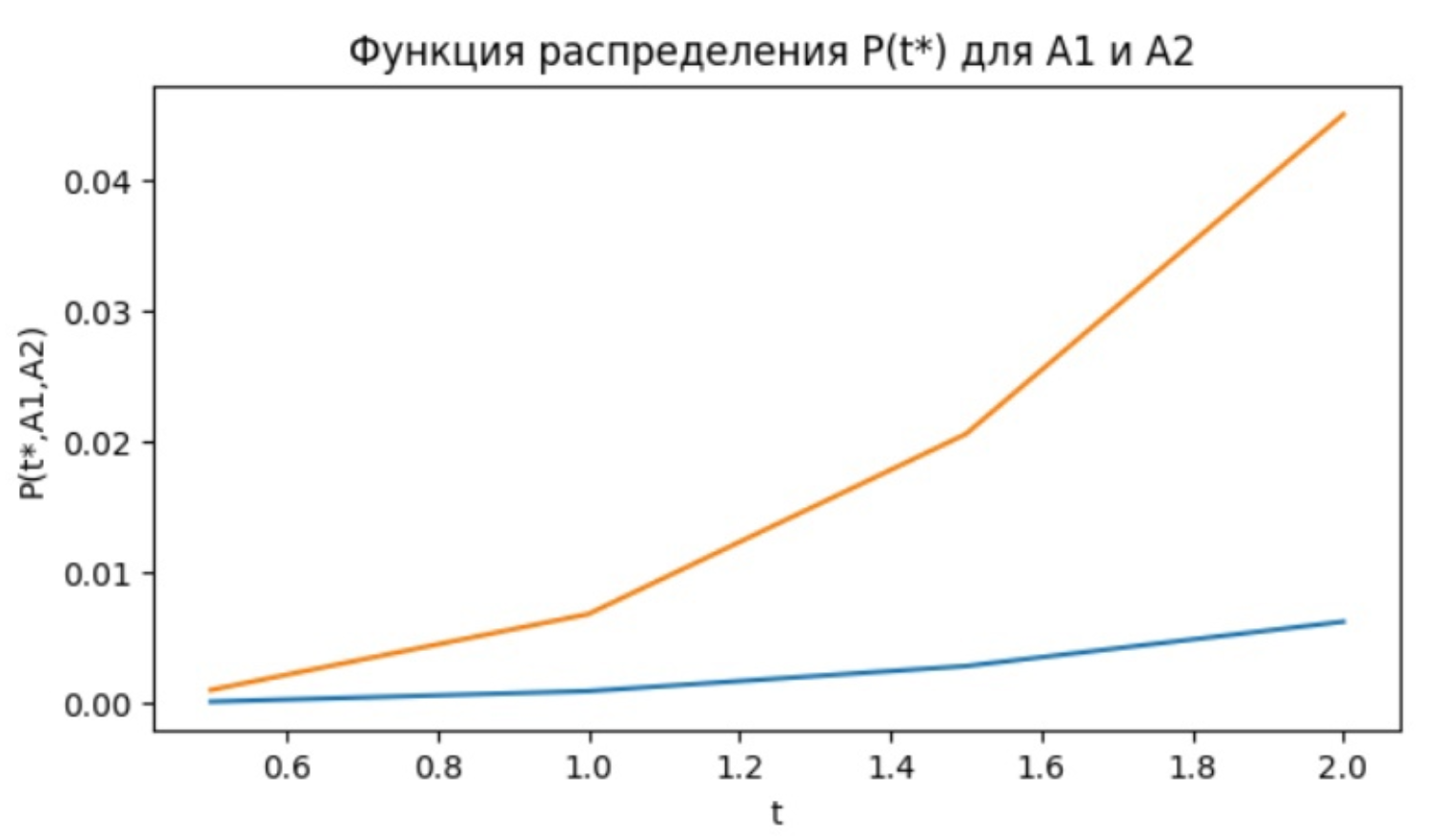



Из графиков видно, что для большей нагрузки мы имеем меньшую вероятность поступления 4 вызовов за одинаковые промежутки времени.

Функция распределения промежутков времени между последовательными моментами поступления вызовов

Чтобы посчитать распределение промежутков времени между моментами поступления вызовов, напишем следующий код программы:

import math
for A in (0.45, 0.93):

print("A = " + str(A) + ":")

for t in (0, 0.1, 0.2, 0.3, 0.4, 0.5):

F = round(1 - (math.exp(-A * t)), 4)
print('F(' + str(t) + ") = " + str(F))

Занесем в таблицу

t*	0	0,1	0,2	0,3	0,4	0,5
F(t*,А1)	0	0.044	0.0861	0.1263	0.1647	0.2015
F(t*,А2)	0	0.0888	0.1697	0.2435	0.3106	0.3719

И построим соответствующие графики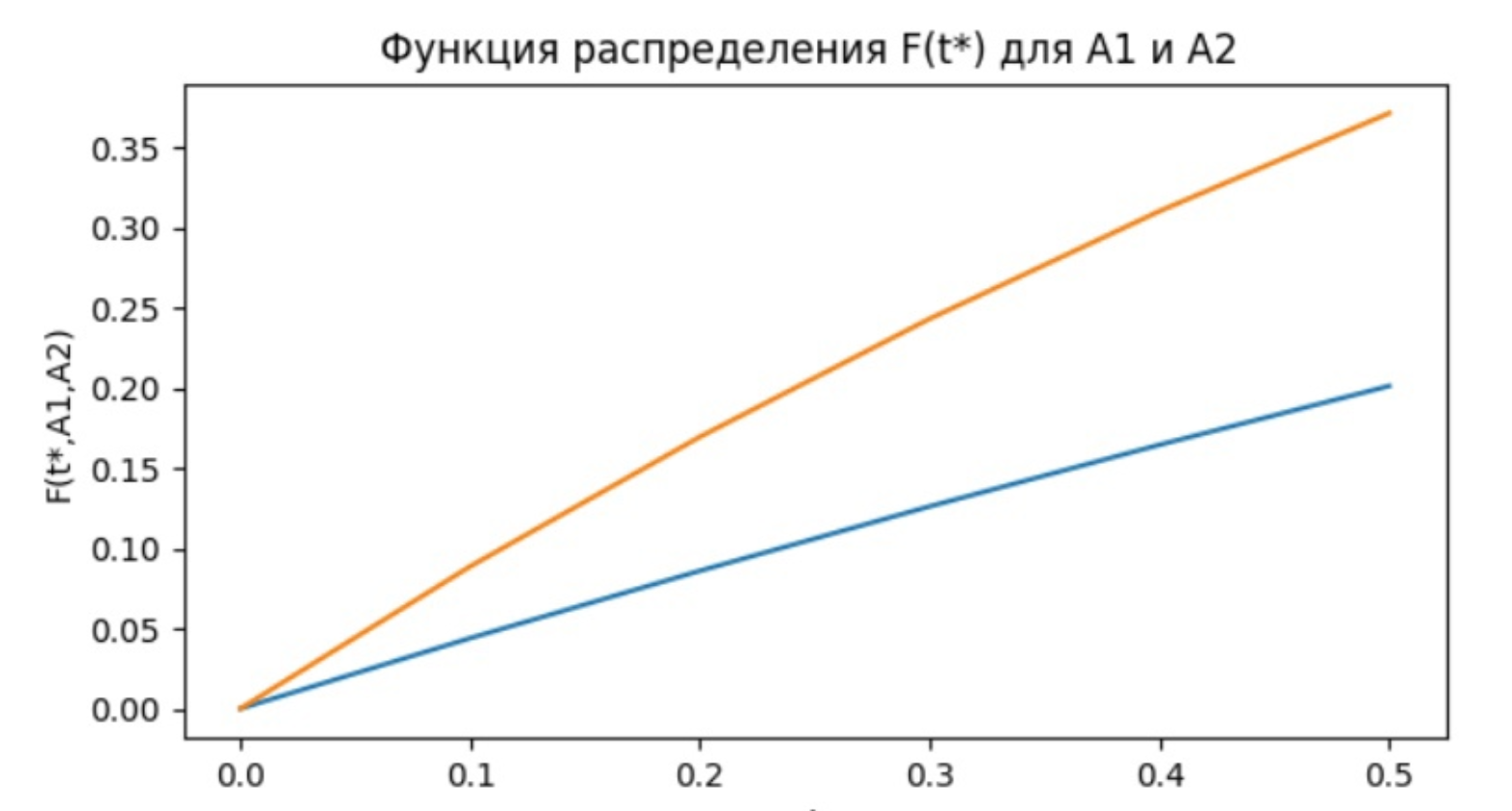



Как видно из графика, распределение времени между моментами поступления вызовов выше для случая, когда нагрузка на сеть больше.

Вероятность поступления не менее kвызовов за интервал времени

Рассчитаем вероятность поступления не менее 4вызовов за интервал времени [0,1) P_i≥k(t^*), где t^*=1. Используем для этого следующую формулу: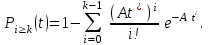

, где k=4, а i>=4.

Вероятность того, что поступит больше 4 вызовов для линий с нагрузкой А1 и А2:

import math

t=1

k=5

for A in (0.45, 0.93):

sum = 0

print("A = " + str(A) + ":")

for j in (0,1,2,3,4):

sum+=((A**j)*math.exp(0-A))/math.factorial(j)

P=round(1-sum,4)

print("Pi>k = " + str(P))
Вывод:

A = 0.45:

Pi>k = 0.7873

A = 0.93:

Pi>k = 0.9827

Вывод

В ходе работы были изучены способы задания потоков вызовов и их свойства (стационарность, ординарность, последействие или его отсутствие). Была рассчитана вероятность поступления 4 вызовов за промежуток времени для простейшего потока вызовов, построен график распределения вероятности. Для большей нагрузки мы имеем меньшую вероятность поступления 4 вызовов за одинаковые промежутки времени.

Также была построена функция распределения промежутков времени между последовательными моментами поступления вызовов. Результаты графиков говорят о том, что распределение времени между моментами поступления вызовов выше для случая, когда нагрузка на сеть больше.

Кроме этого была рассчитана вероятность поступления не менее 4вызовов за интервал времени для разно нагрузки на сеть. Для сети с большей нагрузкой такая вероятность больше.