Машинное обучение. Отчёт_Петрова_Софья_9373. Отчет по практическим работам по дисциплине Машинное обучение
 Скачать 2.91 Mb. Скачать 2.91 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра информационных систем отчет по практическим работам по дисциплине «Машинное обучение»
Санкт-Петербург 2021 Практическая работа 1    Результат: 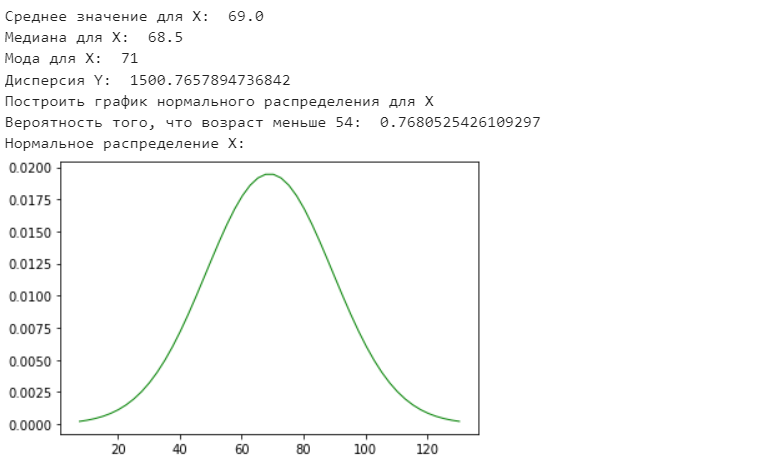 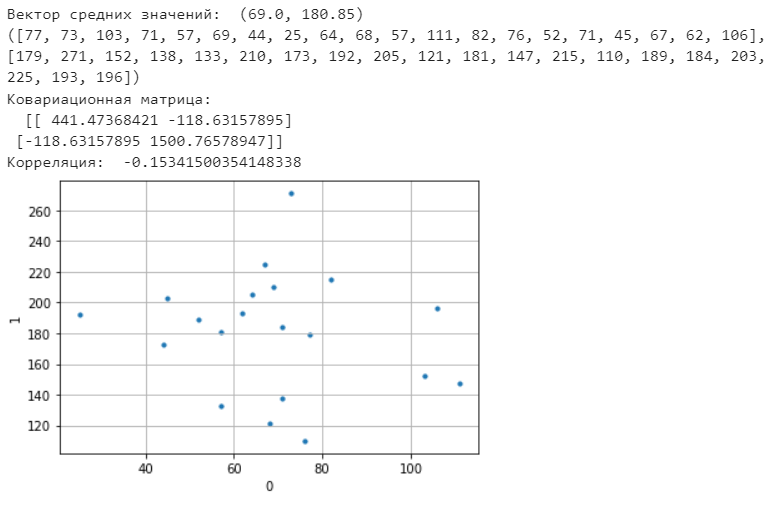   Выводы: В ходе выполнения практической работы для заданных выборок X и Y были найдены среднее выборочное, медиана и мода для величины X, дисперсия для Y. Был построен график нормального распределения для X. Была найдена вероятность того, что возраст (X) меньше 54 (0.768). Также была вычислено двумерное математическое ожидание и ковариационная матрица для X и Y, между ними была определена корреляция, на основании этого построена диаграмма рассеяния, которая отображает зависимость между возрастом и ростом (X и Y). Для набора данных из задания 2 была рассчитана ковариационная матрица и обобщённая дисперсия. Также для данных из 3 задания было для каждого из значений {2,7,11} определено, какое из данных распределений сгенерировало бы значение с большей вероятностью. Кроме того, были найдены два значения, которые могли быть сгенерированы обоими распределениями с равной вероятностью. Практическая работа 2     Результат: 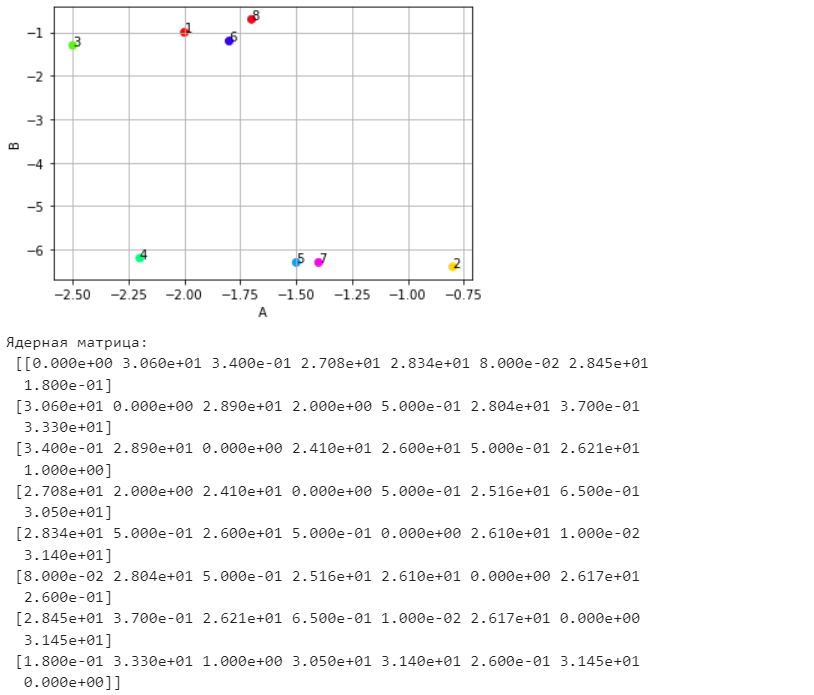 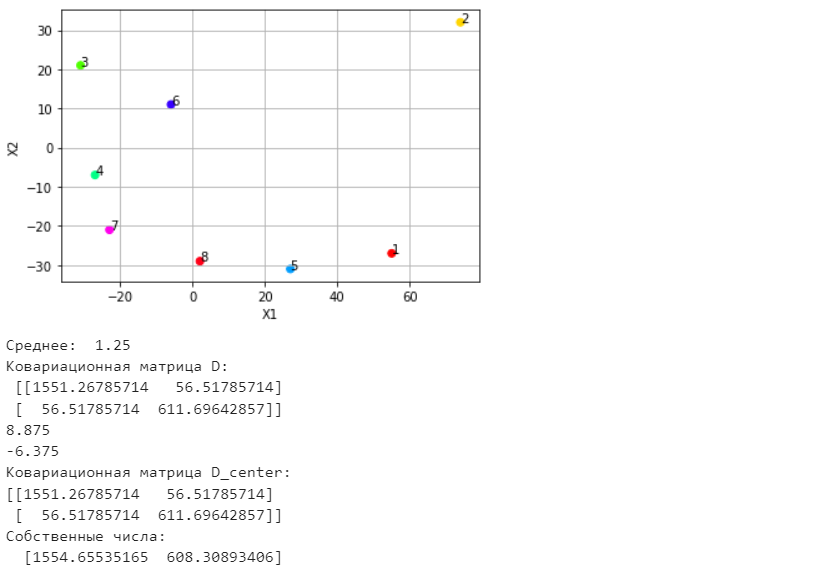 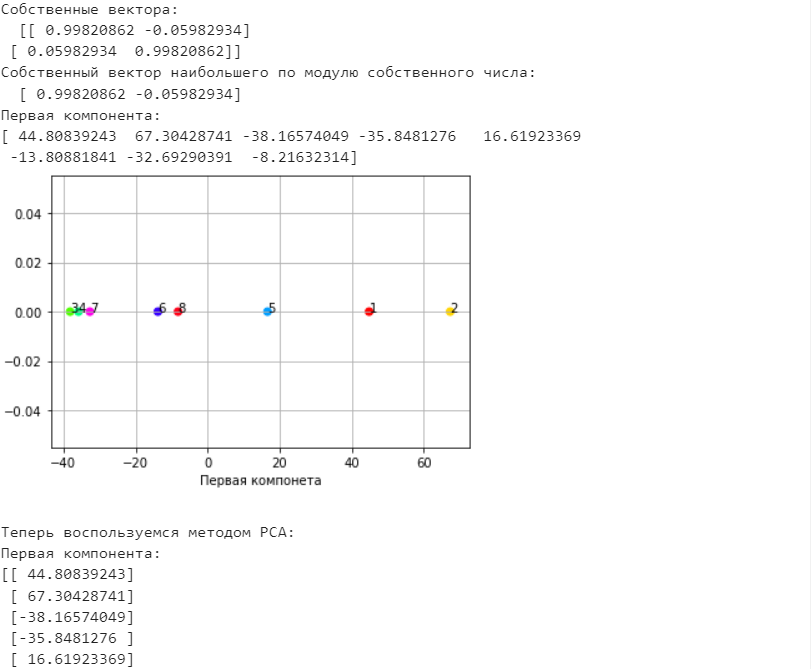 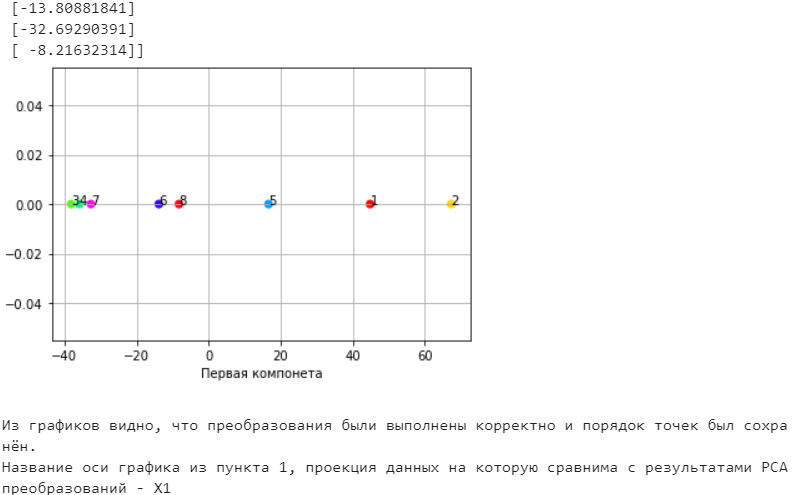 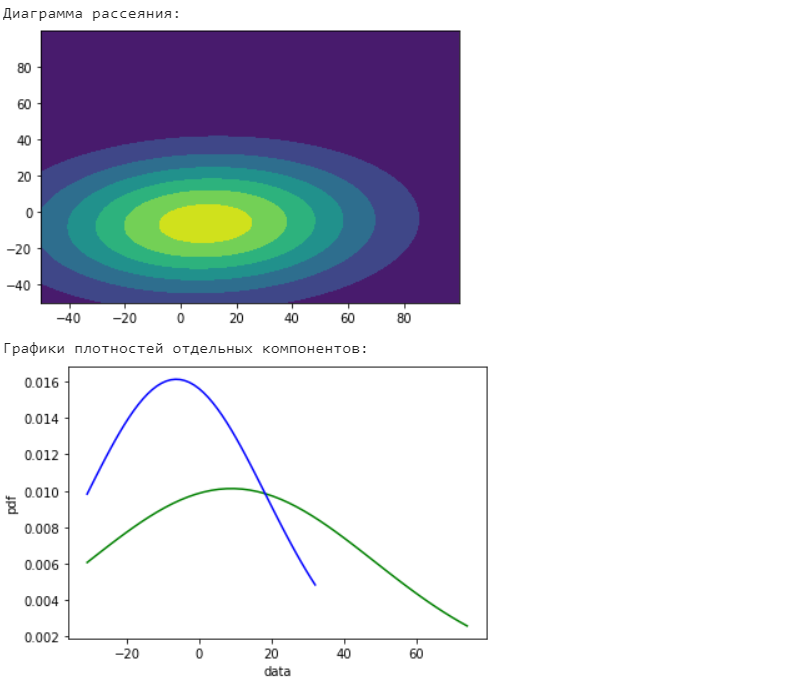  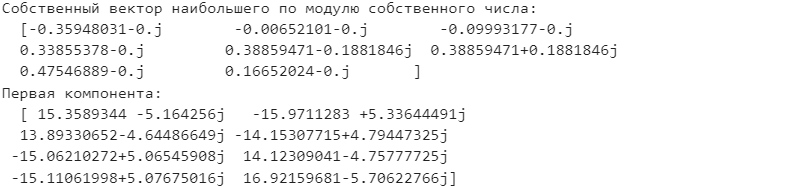 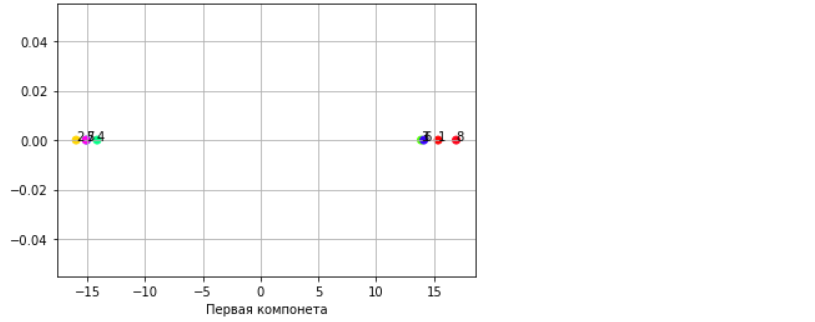 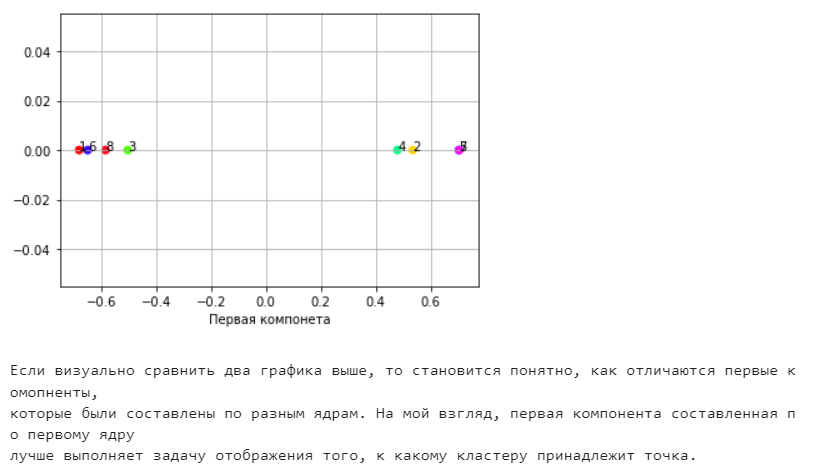 Выводы: В ходе практической работы при заданных данных была построена диаграмма рассеяния точек, а также была рассчитана ядерная матрица при данном ядре. Для данных из второго задания была также построена диаграмма рассеяния. Было рассчитано выборочное среднее, а также ковариационная матрица для исходных данных и ковариационная матрица для центрированных исходных данных. Для ковариационной матрицы от центрированных данных были рассчитаны собственные числа и вектора. Был найден и выведен индекс, который соответствовал первой компоненте (0). Была рассчитана первая главная компонента и по ней построен график. При помощи PCA из библиотеки sklearn была также получена первая главная компонента. После сравнения двух компонент полученных разными способами различий найдено не было. Значит, первая компонента была найдена верно. Кроме того, была построена диаграмма рассеяния, которая позволяет определить ориентацию/размеры облака точек, полученного с помощью 2-мерной функции плотности вероятности. На отдельном линейном графике были построены графики функций плотностей вероятности отельных компонентов 2-мерного нормального распределения. Для полученных в первом задании данных была найдена первая компонента при нелинейном преобразовании для заданного ядра. Результат был отображён в виде точечного графика. При помощи библиотечной функции KernelPCA с ядром Гаусса и гаммой = 1 была высчитана первая главная компонента для полученных в первом задании данных. Также был построен для отображения результатов точечный график. В результате сравнения, есть основания полагать, что первая главная компонента, составленная по первому ядру, лучше выполняет задачу отображения того, к какому кластеру принадлежит точка. Практическая работа 3   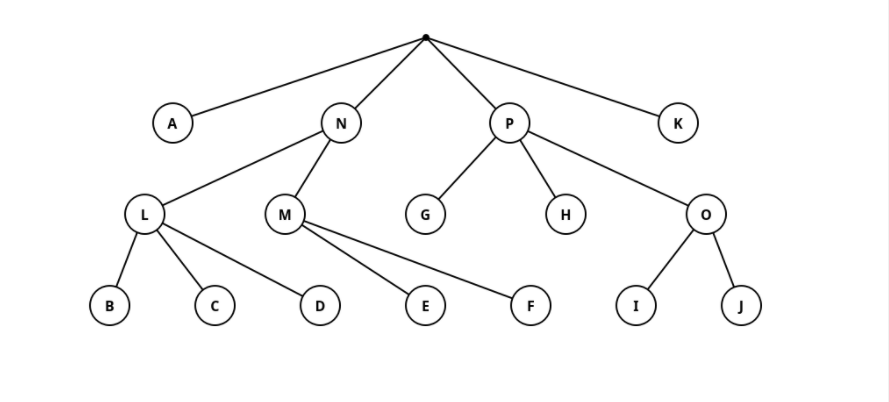   Результат:       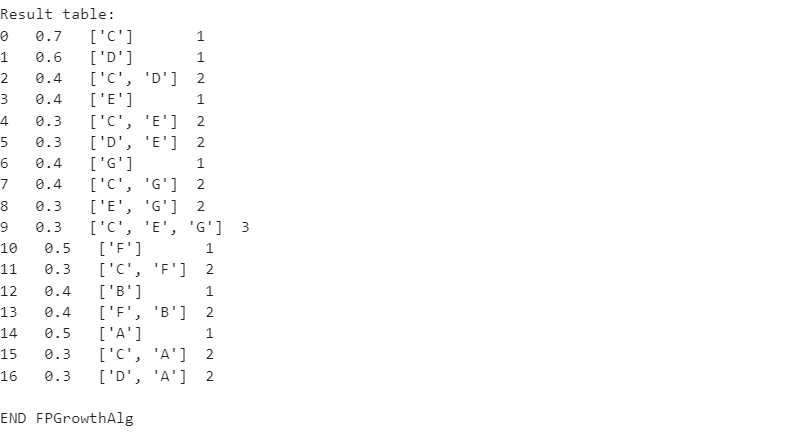 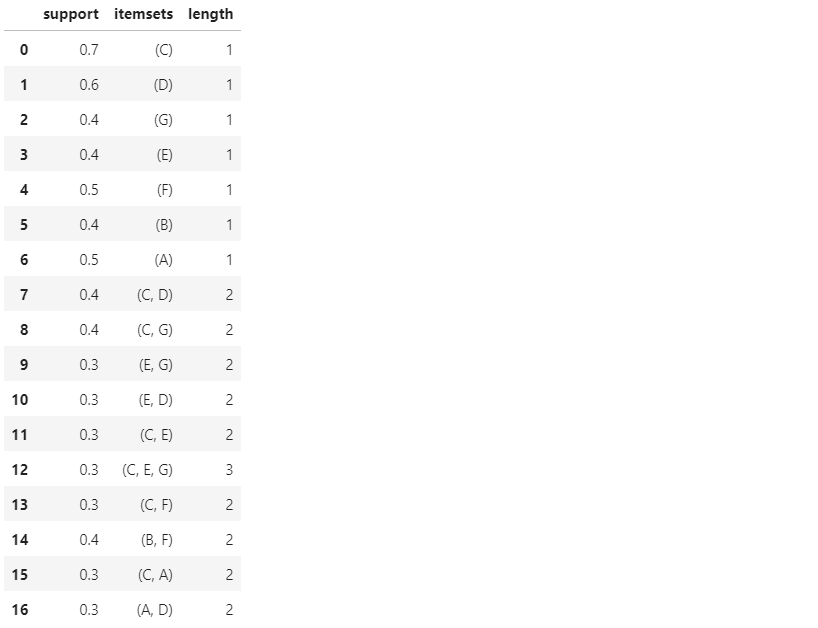  Выводы: В ходе выполнения практической работы при уровне поддержки 4/10 был самостоятельно реализован алгоритм Apriori. Также была подробно представлена работа и результат этого алгоритма. Была использована библиотечная функция Apriori. Результаты собственной реализации и библиотечной функции различий не имели, что подтвердило правильность написания алгоритма. При минимальном уровне поддержки 3/10 был самостоятельно реализован алгоритм FPGrowth. Также была подробно представлена работа и результат этого алгоритма. Так же как для предыдущего алгоритма, была использована библиотечная функция FPGrowth, и результаты работы этих двух функций были сравнены. Возвращенные значения у написанной и библиотечной функций не имели различий, что подтвердило правильность написания алгоритма. Исходя из заданных данных во втором задании, можно сказать, что размер области поиска наборов элементов, если ограничиваться только наборами, которые состоят из простых элементов, равен 11. При минимальном уровне поддержки 3/10 были найдены все часто встречающиеся наборы элементов, которые состоят только из элементов высокого уровня таксономии. Для выполнения этого был задействован алгоритм Apriori. Практическая работа 4 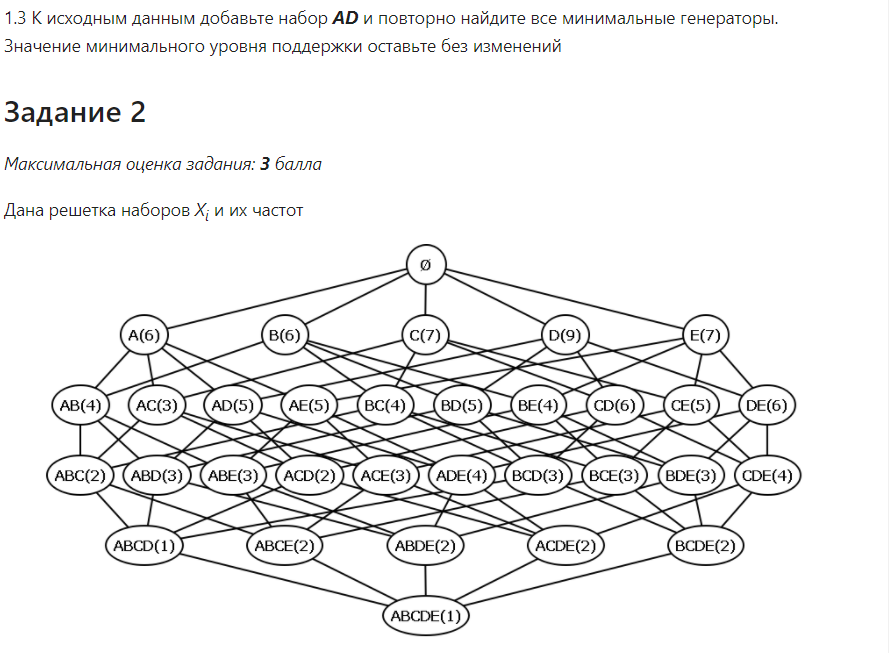    Результат:  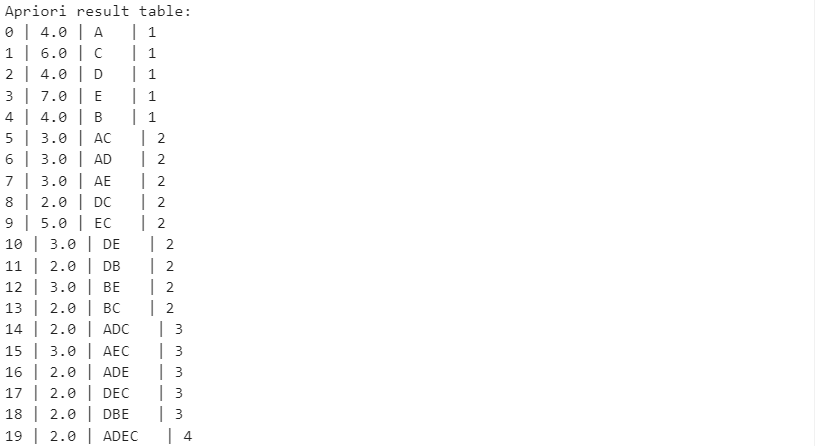 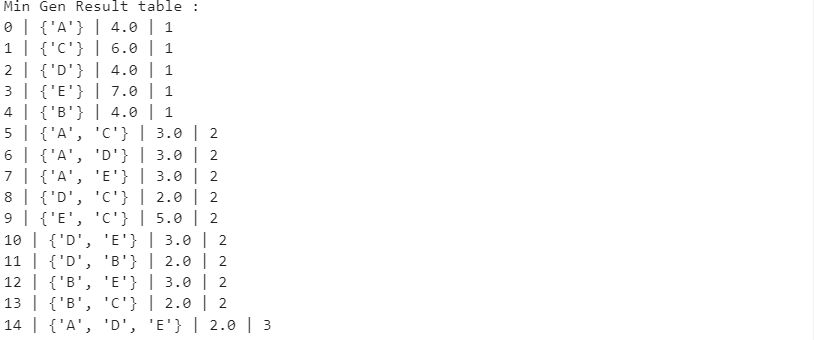               Выводы: В ходе практической работы при помощи написанной в практической работе 3 функции Apriori были найдены самые частые наборы для заданных данных при минимальном уровне поддержке равном 2. Также были найдены в отдельной функции все минимальные генераторы. К исходным данным было добавлено сочетание AD, после этого все минимальные генераторы были найдены заново. При минимальном уровне поддержки 3, используя данную в задании решётку наборов и частот был восстановлен набор данных T. T был отсортирован по заданному ключу (len(Ti), Ti) в порядке возрастания. Был реализован алгоритм Charm. При помощи результатов вычислений был найден список всех закрытых наборов C, он был отсортирован в порядке возрастания. Был пересчитан список всех закрытых наборов после увеличения частоты BD на 1. При минимальном уровне поддержки 4 был реализован алгоритм GSP, найдены все подпоследовательности. Затем к исходным данным была добавлена подпоследовательность TCCTGTAG и повторно найдены все подпоследовательнсоти. Практическая работа 5     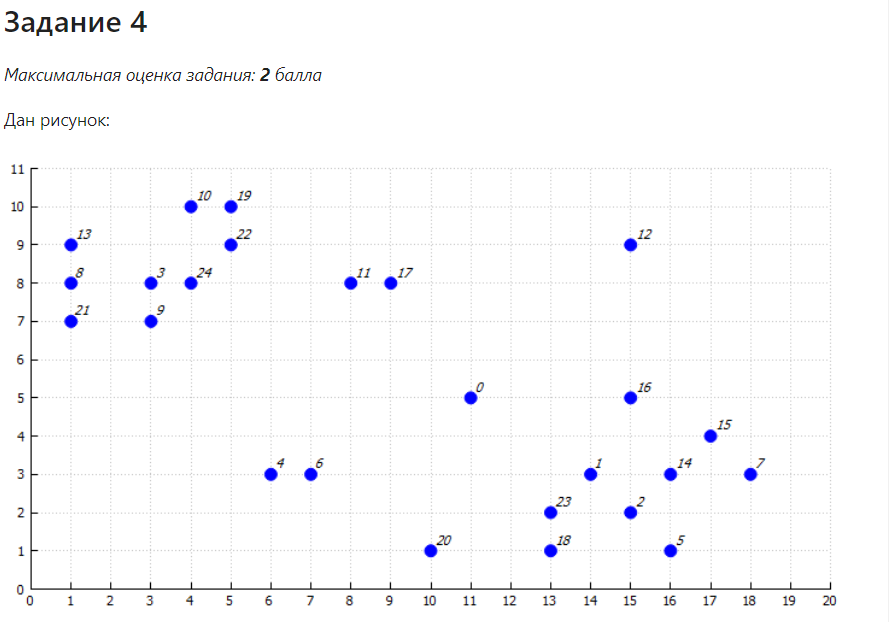   Результаты: 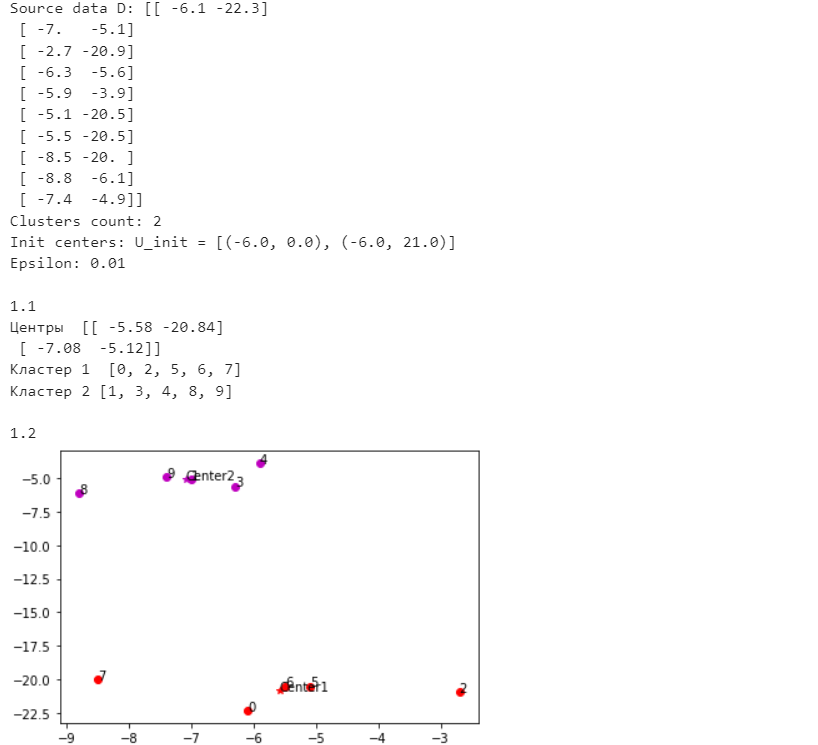   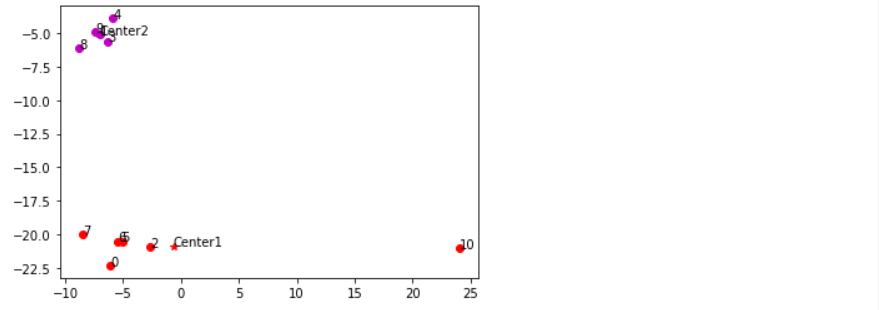    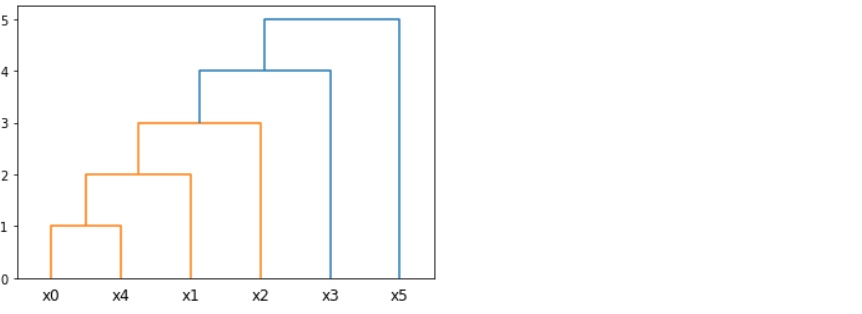  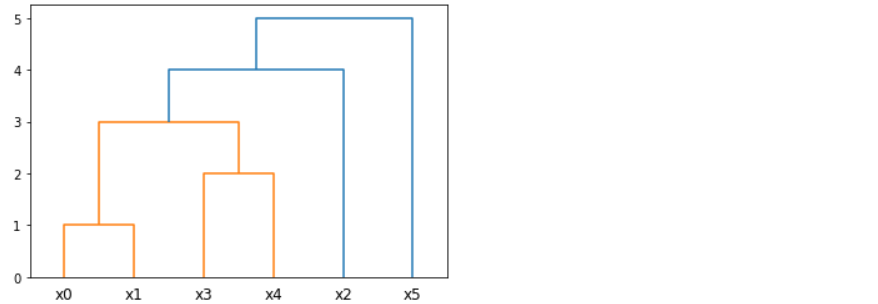 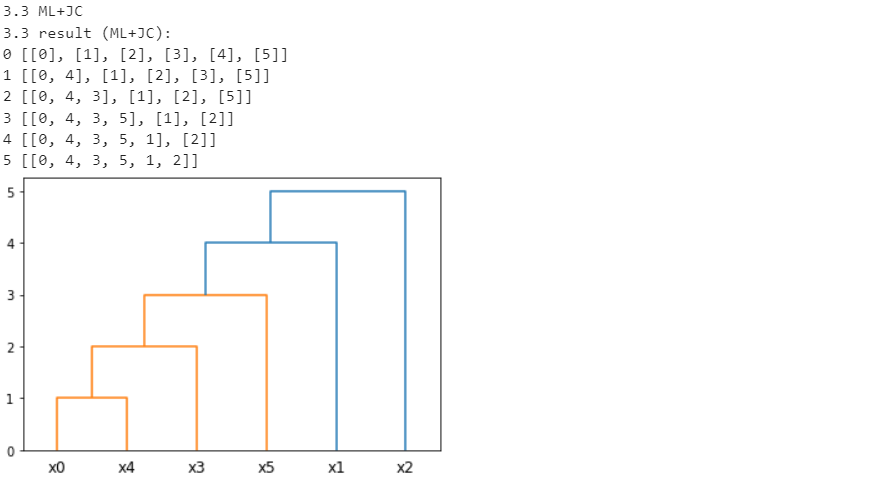  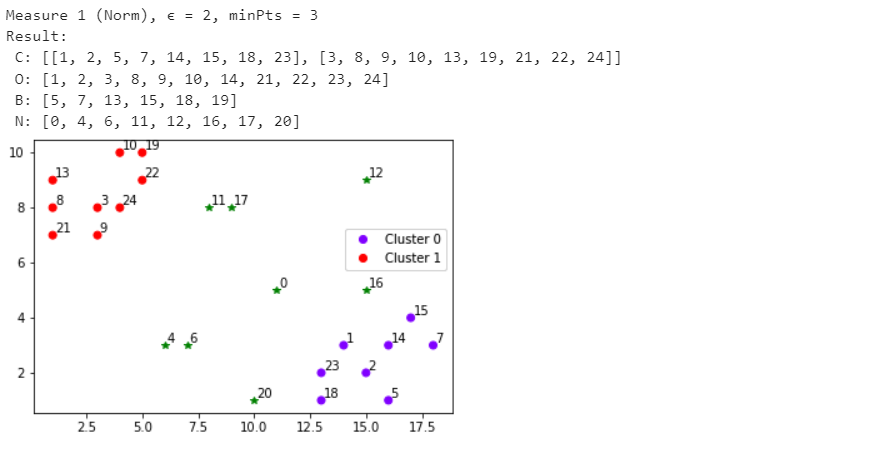 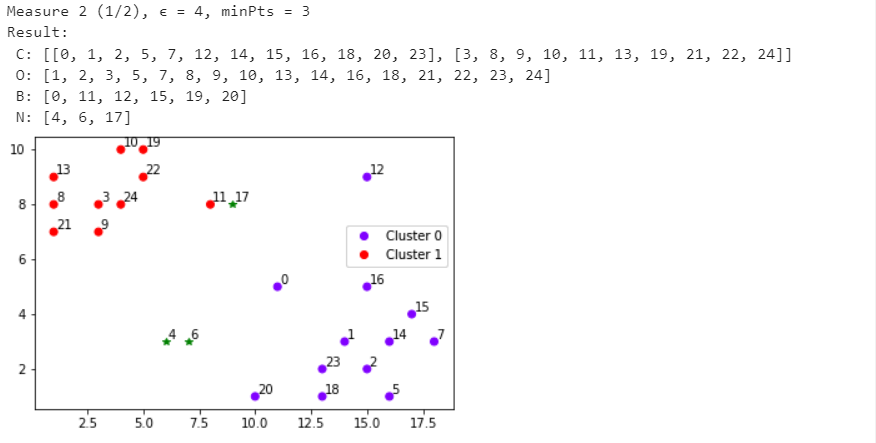 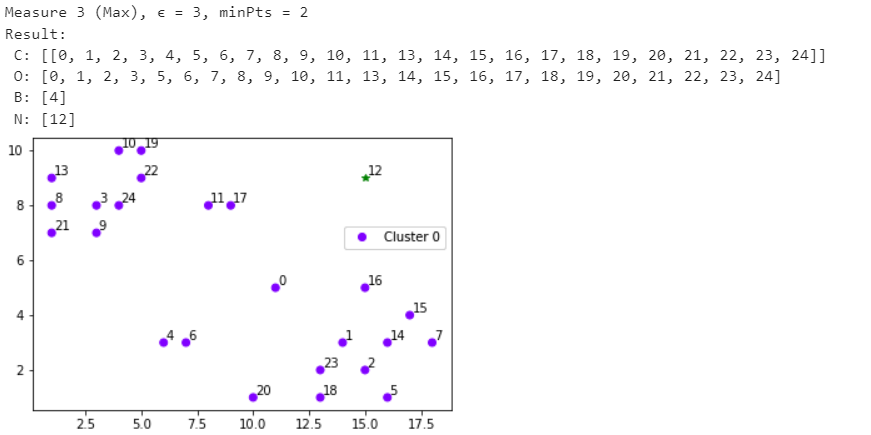 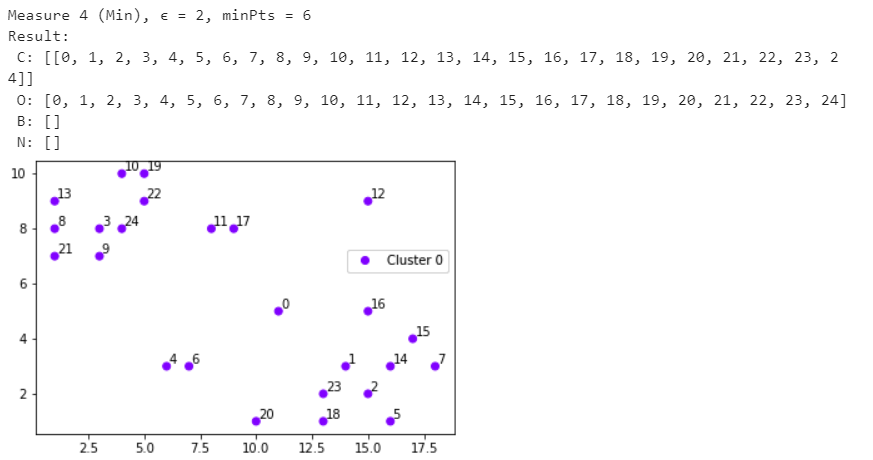 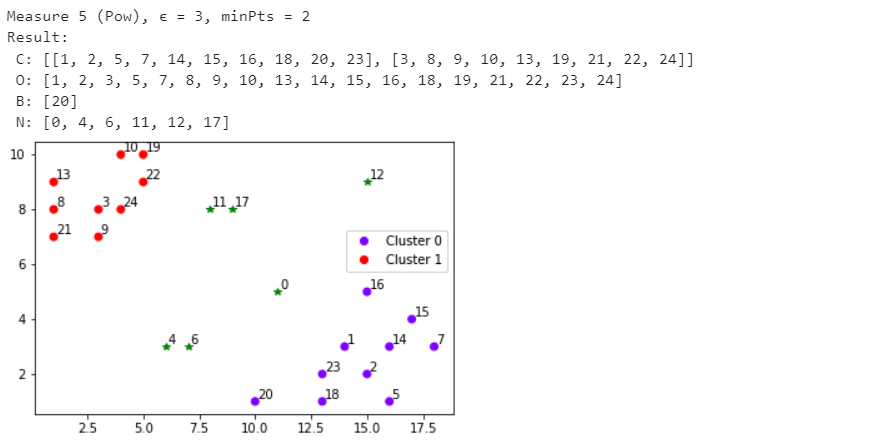 Выводы: В ходе выполнения практической работы был реализован метод разбиения точек на кластеры Kmeans для двумерных данных. Помощи него были вычислены кластеры и центры этих кластеров. На основании этих данных была построена диаграмма рассеяния, где отображены все точки и их принадлежность к кластерам, а также центроиды. При помощи алгоритма Kmeans из библиотеки sklearn были вновь пересчитаны кластеры и их центры. Выяснилось, что результаты написанной самостоятельно функции и библиотечной функции совпадают. Всё то же самое было применено к тем же данным, но с новой точкой. Для заданных данных были найдены оценки максимального правдоподобия для средних. При заданных в задании 2.2 условиях были найдены вероятности принадлежности точки x к первому (0.698) и второму кластеру (0.302). Был реализован алгоритм AgglomerativeClustering. Были выведены результаты в виде списка кластеров, возникающих на каждом шаге алгоритма. Также были построены дендрограммы по результатам кластеризации данных при трех разных параметрах алгоритма. Был реализован алгоритм DBSCAN. Он был применён на данных, а результаты были выведены, в том числе в виде диаграммы рассеяния со всеми необходимыми обозначениями. Также была выполнена кластеризация и построены диаграммы для заданных параметров алгоритма. Практическая работа 6   Результаты: 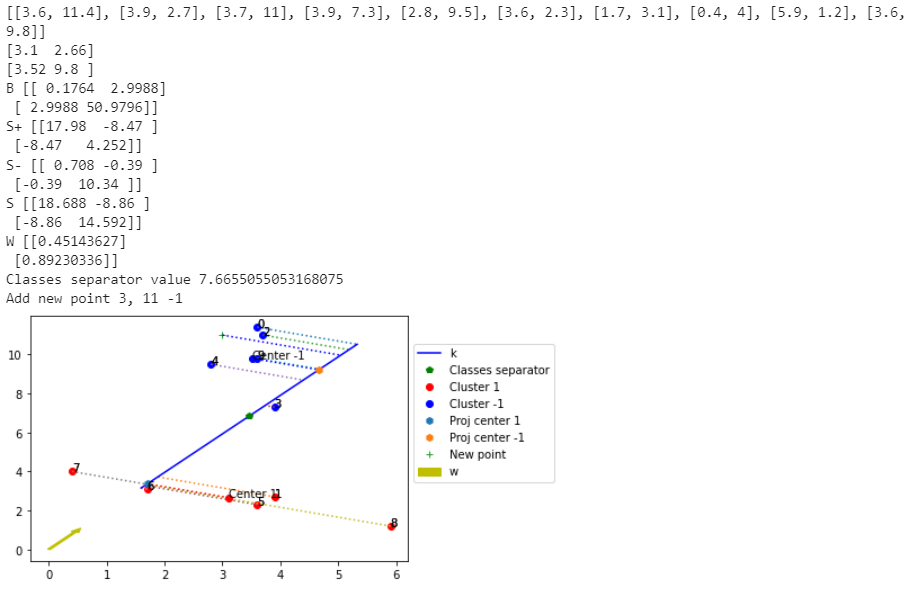 Выводы: В результате выполнения практической работы был реализован линейный дискриминантный анализ для двух классов. Были рассчитаны центры, матрицы межклассового и внутриклассового разбросов, найдено направление w, которое наилучшим образом дискриминирует классы и точка, которая эти классы делит. Также был определён класс для новой точки (-1). Была построена диаграмма рассеяния с необходимыми для понимания обозначениями. |
