PRK1 Горбач. Отчет по практической работе 1 по дисциплине Основы проектирования коммутационных аппаратов и измерительных средств
 Скачать 125.19 Kb. Скачать 125.19 Kb.
|
|
Федеральное агентство железнодорожного транспорта федеральное государственное бюджетное образовательное учреждение высшего образования «Омский государственный университет путей сообщения» (ОмГУПС (ОмИИТ)) Кафедра «Электроснабжение железнодорожного транспорта» НАГРЕВ ТОКОВЕДУЩЕЙ ЧАСТИ Отчет по практической работе №1 по дисциплине «Основы проектирования коммутационных аппаратов и измерительных средств» ИНМВ. 700005. 000 Студент гр. 48-М К. Г. Горбачёв Руководитель – доцент кафедры ЭЖТ В. Л. Незевак Омск 2018 Любой электрический аппарат содержит множество элементов, по одним из которых протекают электрические токи, другие являются проводниками магнитных потоков, третьи служат для электрической изоляции, четвертые перемещаются в пространстве, передавая усилие другим частям. При работе электрического аппарата происходит преобразование одних видов энергии в другие. При этом как известно неизбежны потери энергии, которая превращается в теплоту. Одним из основных источников теплоты в электрических аппаратах является так называемое джоулево тепло. Если имеется однородный проводник, по которому протекает постоянный ток одинаковой во всех точках поперечного сечения проводника плотности, то количество теплоты Р, выделяющегося в проводнике в единицу времени, в соответствии с законом Джоуля-Ленца будет равно 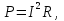 (1) (1)где I – ток в проводнике; R – активное сопротивление проводника. За время dtколичество теплоты составит значение, равное 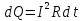 . (2) . (2)Если ток не является постоянным во времени, то за время 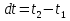 количества теплоты, выделившееся в проводнике, определяется интегрированием: количества теплоты, выделившееся в проводнике, определяется интегрированием: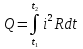 . (3) . (3)Активное сопротивление для однородного проводника равно 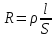 , (4) , (4)где lиS – длина и площадь поперечного сечения проводника. Удельное сопротивление проводника ρ не остается постоянным, а изменяется с изменением температуры по сложной функциональной зависимости, которая при разложении в ряд Тейлора выглядит так 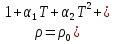 ...). (5) ...). (5)Для большинства проводников при температурах до 200-300°С в практических расчетах можно ограничиться двумя первыми членами формулы (5) и тогда 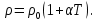 (6) (6)Температурный коэффициент сопротивления α зависит от материала проводника и может быть как положительным, так и отрицательным; 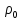 – удельное сопротивление материала проводника при 0°С. – удельное сопротивление материала проводника при 0°С.Если за время 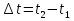 температура проводника изменяется, то значение сопротивления по формуле (3) не будет постоянным. В этом случае расчет количества теплоты необходимо производить с учетом этого изменения. температура проводника изменяется, то значение сопротивления по формуле (3) не будет постоянным. В этом случае расчет количества теплоты необходимо производить с учетом этого изменения.Если проводник неоднородный или плотность тока не постоянна по сечению проводника, то количество теплоты, выделяющегося в проводнике за единицу времени, можно определить по формуле 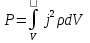 , (7) , (7)где V – объем проводника; j – плотность тока в данной точке поперечного сечения. Если температура проводника изменяется во времени, то количество теплоты за время 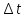 будет равно 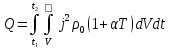 . (8) . (8)Последняя формула является наиболее общей, однако для практических расчетов она трудоемка. Наиболее часто применяется формула (1), в которой сопротивление R представляют в виде 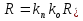 , (9) , (9)где  – сопротивление однородного проводника постоянному току. Коэффициенты – сопротивление однородного проводника постоянному току. Коэффициенты 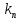 и и 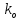 учитывают влияние поверхностного эффекта и эффекта близости соответственно. учитывают влияние поверхностного эффекта и эффекта близости соответственно. Как известно из теоретических основ электротехники, поверхностным эффектом называется явление неравномерного распределения плотности переменного тока попоперечному сечению проводника. Так как в хорошо проводящей среде значением токов смещения по сравнению с токами проводимости можно пренебречь, то уравнение электропроводного поля Максвелла можно записать в виде 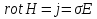 ; (10) ; (10)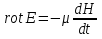 , (11) , (11)где 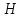 , ,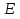 – векторы напряженности магнитного и электрического полей соответственно; – векторы напряженности магнитного и электрического полей соответственно;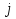 – вектор плотности тока; – вектор плотности тока; 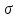 и и 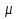 – удельная электрическая проводимость среды и ее магнитная проницаемость. – удельная электрическая проводимость среды и ее магнитная проницаемость.Явление поверхностного эффекта, которое следует рассматривать как процесс проникновения электромагнитного поля в проводник из окружающего его пространства, довольно трудно подается аналитическому описанию. Для простейшего случая прямолинейного уединенного проводника круглого поперечного сечения в курсе ТОЭ выводится формула, выражающая зависимость комплексной амплитуды плотности тока 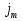 от расстояния от расстояния 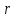 , от оси проводника и от значения комплексной амплитуды плотности тока , от оси проводника и от значения комплексной амплитуды плотности тока 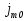 , на оси проводника , на оси проводника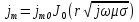 , (12) , (12)где 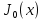 – бесселева функция первого рода нулевого порядка; – бесселева функция первого рода нулевого порядка; 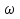 – угловая частота переменного тока. – угловая частота переменного тока.Физику явления поверхностного эффекта можно объяснить следующим образом. Если в цилиндрическом проводнике выделить два одинаковых по длине и поперечному сечению проводника: один на оси, а другой на периферии поперечного сечения, то их активные сопротивления будут равны друг другу. Так как индуктивность проводника можно определить как 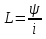 , (13) , (13)где 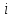 – ток в проводнике, а ψ – его потокосцепление, то легко видеть что индуктивность проводника, находящегося на периферии, меньше, чем индуктивность осевого проводника, так как периферийный проводник охватывается меньшим числом магнитных силовых линий, чем – ток в проводнике, а ψ – его потокосцепление, то легко видеть что индуктивность проводника, находящегося на периферии, меньше, чем индуктивность осевого проводника, так как периферийный проводник охватывается меньшим числом магнитных силовых линий, чемосевой. Следовательно, 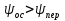 и и 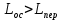 . Тогда полные сопротивления проводников будут находиться в соотношении . Тогда полные сопротивления проводников будут находиться в соотношении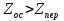 . (14) . (14)Предполагая равенство падений напряжения на обоих проводниках, легко увидеть, что ток в осевом проводнике будет меньше тока периферийного проводника. Ток вытесняется из центра проводника к его поверхности. Неравномерность распределения плотности тока эквивалентна «недоиспользованию» внутренних зон проводника для проведения тока, и, следовательно, к увеличению сопротивления проводника. Это приводит к возникновению дополнительных по сравнению с постоянным током потерь, которые в формуле (9) учитываются коэффициентом поверхностного эффекта 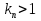 (рисунок 1а). (рисунок 1а).В проводниках из ферромагнитного материала явление поверхностного эффекта проявляется значительно сильнее. Объяснить это можно тем, что плотность магнитных силовых линий в ферромагнитном материале в силу большой магнитной проницаемости значительно больше, чем в неферромагнитном. Следовательно, глубина проникновения электромагнитного поля значительно меньше. Для большинства ферромагнитных материалов при частоте 50 Гц она измеряется десятыми долями миллиметра. При протекании тока по ферромагнитному проводнику он будет сосредоточен в поверхностном слое проводника, толщина которого равна глубине проникновения электромагнитного поля 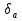 . Тогда в соответствии с формулой (1) потери энергии в проводнике единичной длины будут равны . Тогда в соответствии с формулой (1) потери энергии в проводнике единичной длины будут равны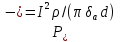 . (15) . (15)Так как потери энергии при постоянном токе равны 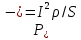 , то коэффициент поверхностного эффекта для данного случая будет равен , то коэффициент поверхностного эффекта для данного случая будет равен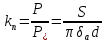 , (16) , (16)где 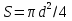 ;d– диаметр проводника. ;d– диаметр проводника.Значение величины 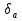 зависит от магнитной проницаемости материала проводника и от значения напряженности магнитного поля, а следовательно, и от значения протекающего тока. зависит от магнитной проницаемости материала проводника и от значения напряженности магнитного поля, а следовательно, и от значения протекающего тока.Профессором Н. Е. Лысовым предложена эмпирическая формула для вычисления мощности потерь при протекании переменного тока по проводникам из ферромагнитного материала 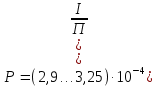 , (17) , (17)где 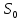 , , 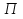 – площадь поверхности и периметр поперечного сечения проводника соответственно; – площадь поверхности и периметр поперечного сечения проводника соответственно;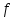 – частота тока; – частота тока;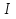 – протекающий по проводнику переменный ток. – протекающий по проводнику переменный ток.Формула (17) дает наиболее приемлемые результаты при больших напряженностях магнитного поля, когда наименьший размер поперечного сечения проводника больше удвоенной глубины проникновения электромагнитного поля. Эффектом близости называется явление изменения распределения плотности переменного тока по сечению проводника, обусловленное влиянием близко расположенных проводников с токами. Пусть имеется два близко расположенных параллельных проводника, по которым протекают переменные токи 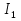 и и 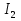 (рисунок 1). Для случая, изображенного на рисунке 1а, магнитный поток (рисунок 1). Для случая, изображенного на рисунке 1а, магнитный поток 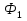 , обусловленный током , обусловленный током 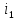 , будет пронизывать проводник с током , будет пронизывать проводник с током 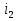 . В проводнике 2 возникнут токи, направленные в соответствии с законом Ленца так, чтобы вызванный ими магнитный поток препятствовал изменению потока . В проводнике 2 возникнут токи, направленные в соответствии с законом Ленца так, чтобы вызванный ими магнитный поток препятствовал изменению потока 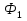 . Индуцированные токи . Индуцированные токибудут векторно складываться с током 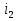 , что приведет к перераспределению плотности тока в проводнике 2. , что приведет к перераспределению плотности тока в проводнике 2. На рисунке 1а пунктирными линиями изображено распределение плотности тока в проводниках, обусловленное только поверхностным эффектом. Сплошные линии соответствуют плотности тока при влиянии эффекта близости. Аналогично можно объяснить распределение плотности тока и в проводнике 1, а также и распределение плотности тока в проводниках 1 и 2, когда токи в них протекают в противоположных направлениях (рисунок 1б). При тепловых расчетах неравномерность плотности тока, вызванная этими эффектами, учитывается зависимостью 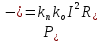 . (18) . (18)В общем случае коэффициент близости, так же как и коэффициент поверхностного эффекта, зависит от параметра 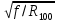 , геометрических размеров, формы проводников и от расстояния между ними. В отличие от коэффициента поверхностного эффекта коэффициент близости может быть как больше, так и меньше или равным единице. , геометрических размеров, формы проводников и от расстояния между ними. В отличие от коэффициента поверхностного эффекта коэффициент близости может быть как больше, так и меньше или равным единице.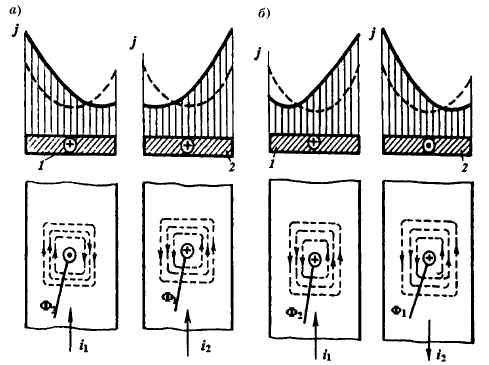 Рисунок 1 – К эффекту близости в двух параллельно расположенных шинах На рисунках 2 и 3 приведены зависимости 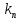 и и 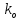 от параметров проводников и частоты тока (d– диаметр круглого проводника; h, l, от параметров проводников и частоты тока (d– диаметр круглого проводника; h, l, 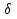 – размеры прямоугольного шинопровода; – размеры прямоугольного шинопровода; 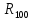 – сопротивление проводника длиной 100 м; – сопротивление проводника длиной 100 м; 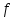 – частота тока, Гц). В литературных источниках содержатся данные по – частота тока, Гц). В литературных источниках содержатся данные по 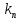 и и 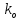 для большинства встречающихся на практике случаев. для большинства встречающихся на практике случаев.В ферромагнитных нетоковедущих частях, находящихся в переменном магнитном поле, также выделяется теплота, что обусловлено вихревыми токами, возникающими в том случае, когда изменяющийся во времени магнитный поток пронизывает ферромагнитные части аппарата или других устройств. В сплошном замкнутом магнитопроводе, охватывающем проводник, расчет потерь можно производить по приближенной формуле (17), в которой вместо тока Iнеобходимо подставить магнитодвижущую силу IN, а вместо периметра П — среднюю длину магнитопровода 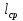 . .Если магнитопровод выполнен из листовой стали, то источники теплоты в нем определяются на основании приведенных в справочной литературе зависимостей удельных потерь от амплитудного значения индукции, частоты тока, толщины и сорта стали. Ферромагнитные части нагреваются в переменном магнитном поле, даже если они не образуют замкнутую систему для магнитного потока. Так, в случае стальной балки, перпендикулярно которой на некотором расстоянии от нее расположен проводник с переменным током, предполагают, что вихревые токи, обусловленные переменным магнитным полем, протекают в слое балки на глубине проникновения электромагнитного поля 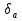 . Количество теплоты, которое выделяется в балке в этом случае, определяется по формуле . Количество теплоты, которое выделяется в балке в этом случае, определяется по формуле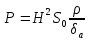 , (19) , (19)где 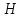 – составляющая напряженности магнитного поля, направленная вдоль оси балки; – составляющая напряженности магнитного поля, направленная вдоль оси балки; 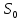 – боковая поверхность балки; – боковая поверхность балки; 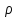 – удельное сопротивление материала балки; – удельное сопротивление материала балки; 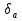 – глубина проникновения магнитного поля. – глубина проникновения магнитного поля.В электрических аппаратах, предназначенных для коммутации электрических цепей, мощным источником теплоты является электрическая дуга, а для ряда аппаратов и их элементов дуга является основным источником теплоты. Во многих аппаратах потери на трение или удар составляют значительную долю от общих потерь энергии. Например, в электромагнитных муфтах преобладают потери на трение. Электрические аппараты, содержащие перемещающиеся жидкости или газы, должны быть рассчитаны с учетом гидравлических потерь. Источником теплоты в аппаратах могут стать диэлектрические потери в изоляционных элементах. Первыйвид этих потерь определяется движением свободных за рядов в диэлектрике и зависит от приложенного напряжения и активного электрического сопротивления диэлектрика (джоулева теплота). Второй вид потерь вызван вязкостью диэлектрика, в котором происходит поворот полярных молекул в направлении электрического поля. Эти потери существенно зависят от частоты изменения направления электрического поля. 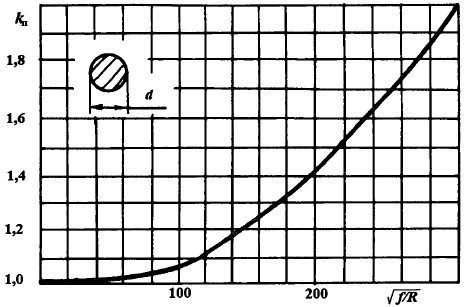 Рисунок 2 – Зависимость 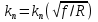 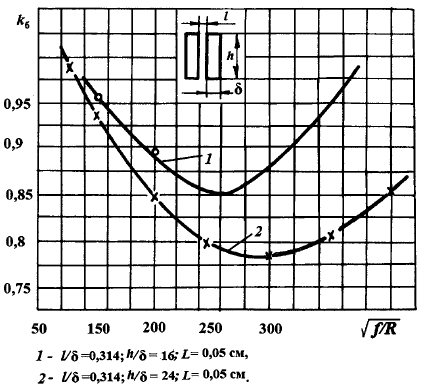 Рисунок 3 – Кривые коэффициента близости Таблица 1 – Исходные данные (вариант 5)
Задание №1:
Задание №2 и 3:
Задание №4: Коэффициент теплоотдачи меди – 0,07 Коэффициент сопротивления меди – 0,018
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
