Сиаод мирэа 2 семестр. Отчёт_2. Отчет по практической работе 2 Оценка сложности и определение эффективности алгоритма по дисциплине Структуры и алгоритмы обработки данных
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА
ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ №2 Оценка сложности и определение эффективности алгоритма по дисциплине «Структуры и алгоритмы обработки данных»
Москва 2023 Содержание Цель работыПриобретение практических навыков, связанных с: определением сложности алгоритмов эмпирическим способом; реализацией алгоритмов сортировки; нахождением эффективного алгоритма решения задачи из нескольких определением емкостной и временной сложностей алгоритма и их зависимости от объема входных данных. Ход работыЗадание 1Формулировка заданияОценить эффективность простого алгоритма сортировки на массиве, заполненном случайными числами (в среднем случае). Используемый алгоритм – Selection Sort. Описание математической моделиИдет проход по массиву с помощью цикла для i. В min записывается значение текущего индекса. С помощью внутреннего цикла происходит поиск минимума и перезапись min. После выполнения внутреннего цикла при неравенстве текущего индекса и min происходит перестановка элементов. Блок-схема алгоритма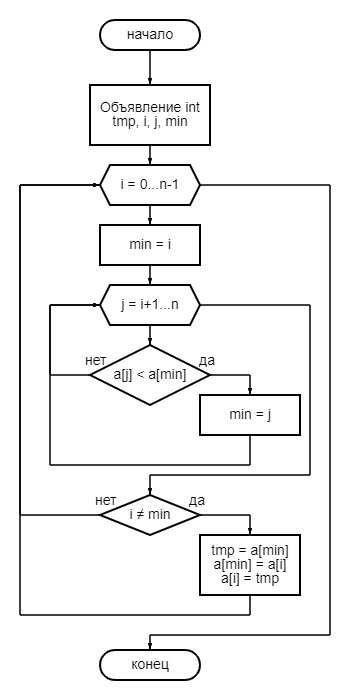  Рисунок 1 – блок-схема алгоритма сортировки Код программы   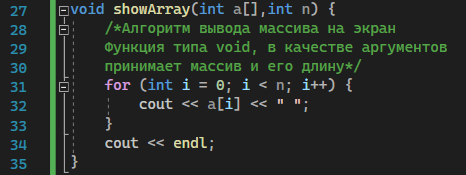  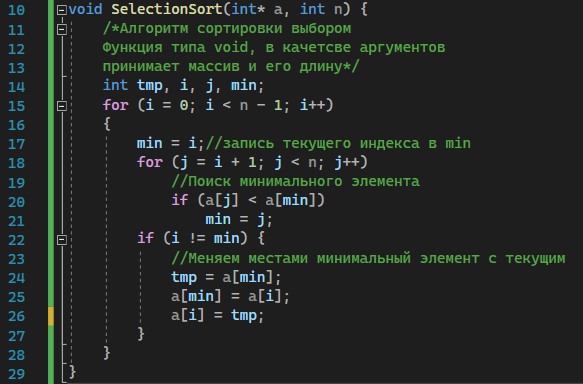 Рисунок 2 – Алгоритм сортировки Рисунок 3 – Функция вывода массива Рисунок 4 – Функция заполнения массива случайными числами 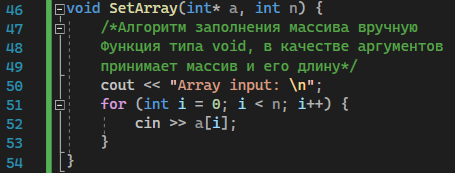     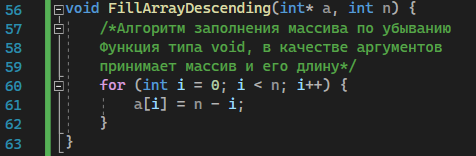 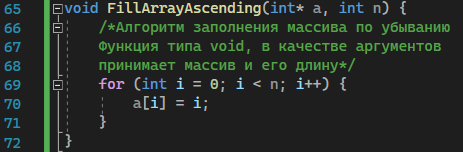 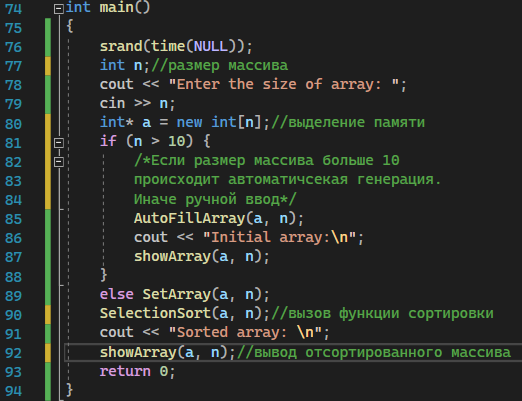 Рисунок 8 – Функция main Рисунок 6 – Функция заполнения массива числами по убыванию Рисунок 5 – Функция ручного заполнения массива Рисунок 7 – Функция заполнения массива числами по возрастанию Тестирование    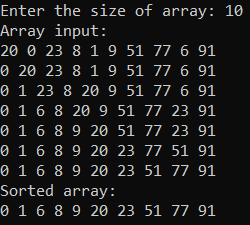 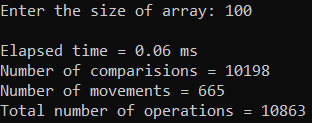 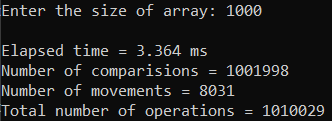 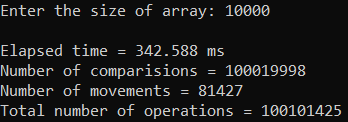 Рисунок 10 – Тестирование при n = 100. Средний случай Рисунок 9 – Тестирование и отладка при n = 10. Рисунок 11 – Тестирование при n = 1000. Средний случай Рисунок 12 – Тестирование при n = 10 000. Средний случай 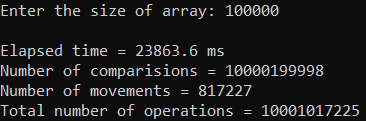  Рисунок 13 – Тестирование при n = 100 000. Средний случай 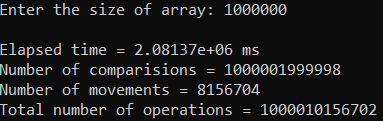  Рисунок 14 – Тестирование при n = 1 000 000. Средний случай Обработка результатовТаблица 1 – Selection Sort, средний случай
Оценка емкостной сложностиИспользуется 1 вспомогательная переменная, необходимая для перестановок. Емкостная сложность: 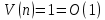 Графики зависимости сложности от nГ 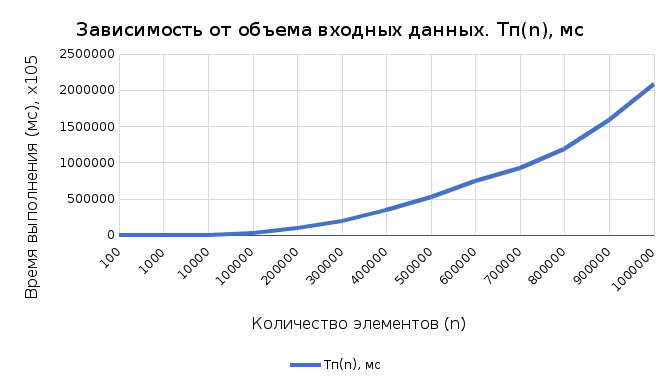 рафик 1 рафик 1Г 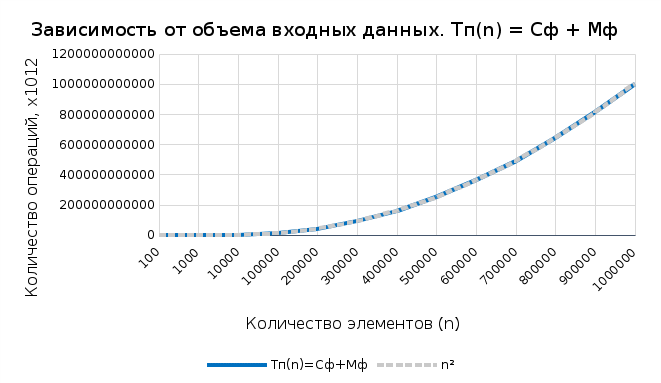 рафик 2 рафик 2 |
| Номер оператора | Оператор | Кол-во выполнений оператора в строке |
| 1 | SelectionSort(int* a, int n) { | |
| 2 | int tmp, i, j, min; | 4 |
| 3 | for (i = 1; i <= n-1; i++) do | n |
| 4 | min = i | n-1 |
| 5 | for (j=i+1; j<=n; j++) do | 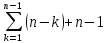 |
| 6 | if (a[j] < a[min]) then | 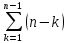 |
| 7 | min = j | 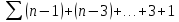 |
| 8 | endif | |
| 9 | od | |
| 10 | if (i != min) then | n-1 |
| 11 | tmp = a[min] | n/2 |
| 12 | a[min] = a[i] | n/2 |
| 13 | a[i] = tmp | n/2 |
| 14 | endif | |
| 15 | od | |
| 16 | } | |
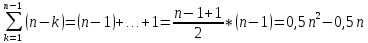
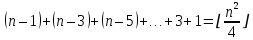
Общая вычислительная сложность алгоритма:
В лучшем случае (массив отсортирован в возрастающем порядке):
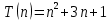
В худшем случае (массив отсортирован в убывающем порядке):
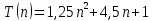
Т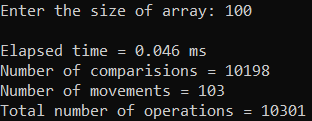 естирование
естирование
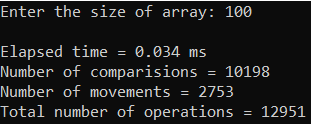







Рисунок 16 – Тестирование при n = 100.
Худший случай
Рисунок 24 – Тестирование при n = 1 000 000.
Худший случай
Рисунок 22 – Тестирование при n = 100 000.
Худший случай
Рисунок 18 – Тестирование при n = 1000.
Худший случай
Рисунок 20 – Тестирование при n = 10 000.
Худший случай
Рисунок 19 – Тестирование при n = 10 000.
Лучший случай
Рисунок 21 – Тестирование при n = 100 000.
Лучший случай



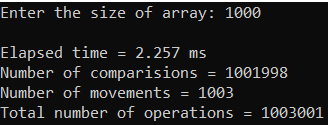
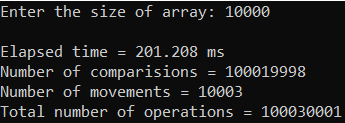
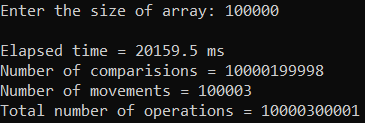
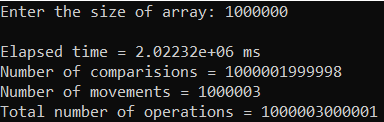
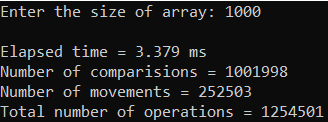
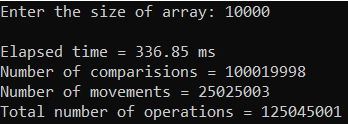
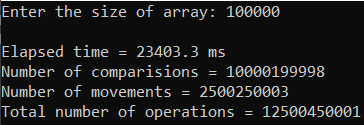
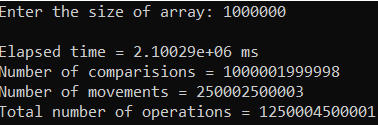
Рисунок 15 – Тестирование при n = 100.
Лучший случай
Рисунок 17 – Тестирование при n = 1000.
Лучший случай
Рисунок 23 – Тестирование при n = 1 000 000.
Лучший случай
Обработка результатов
Лучший случай:
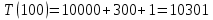
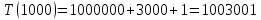
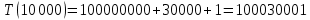
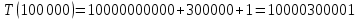
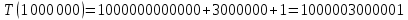
Таблица 2 – Selection Sort, лучший случай
| n | T(n), мс | Тп(n) = Cф + Mф | Тт(n) = С + М |
| 100 | 0,046 | 10 301 | 10 301 |
| 1000 | 2,257 | 1 003 001 | 1 003 001 |
| 10 000 | 201,208 | 100 030 001 | 100 030 001 |
| 100 000 | 20 159,500 | 10 000 300 001 | 10 000 300 001 |
| 1 000 000 | 2 022 320,000 | 1 000 003 000 001 | 1 000 003 000 001 |
Худший случай:
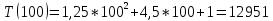
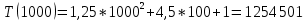
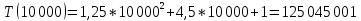
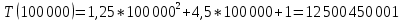
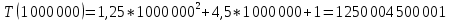
Таблица 3 – Selection Sort, худший случай
| n | T(n), мс | Тп(n)=Cф+Mф | Тт(n)=С+М |
| 100 | 0,014 | 12 951 | 12 951 |
| 1000 | 1,146 | 1 254 501 | 1 254 501 |
| 10 000 | 115,184 | 125 045 001 | 125 045 001 |
| 100 000 | 12 382,100 | 12 500 450 001 | 12 500 450 001 |
| 1 000 000 | 1 536 200,000 | 1 250 004 500 001 | 1 250 004 500 001 |
График зависимости сложности от n
Г
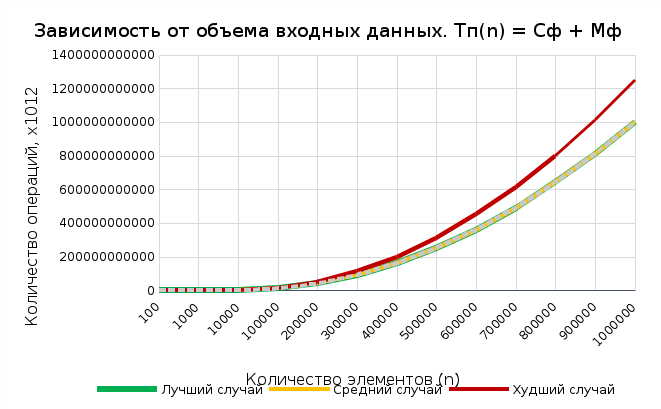 рафик 3
рафик 3Вывод по заданию 2
Полученные данные подтверждают, что сложность алгоритма имеет квадратичный характер вне зависимости от исходного состояния массива. Результаты теоретического расчета и практического выполнения совпали. В худшем случае сложность определяется формулой
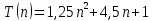 (квадратичная сложность), а в лучшем случае
(квадратичная сложность), а в лучшем случае 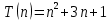 (квадратичная сложность).
(квадратичная сложность).Задание 3
Формулировка задания
Сравнить эффективность двух алгоритмов простых сортировок. Второй используемый алгоритм – Exchange Sort.
Описание математической модели
Осуществляется проход по массиву от 1 элемента до n-ного, сравнивая текущий элемент со всеми последующими. Если какой-то из последующих элементов меньше i-того, то меняем их местами.
Блок-схема алгоритма

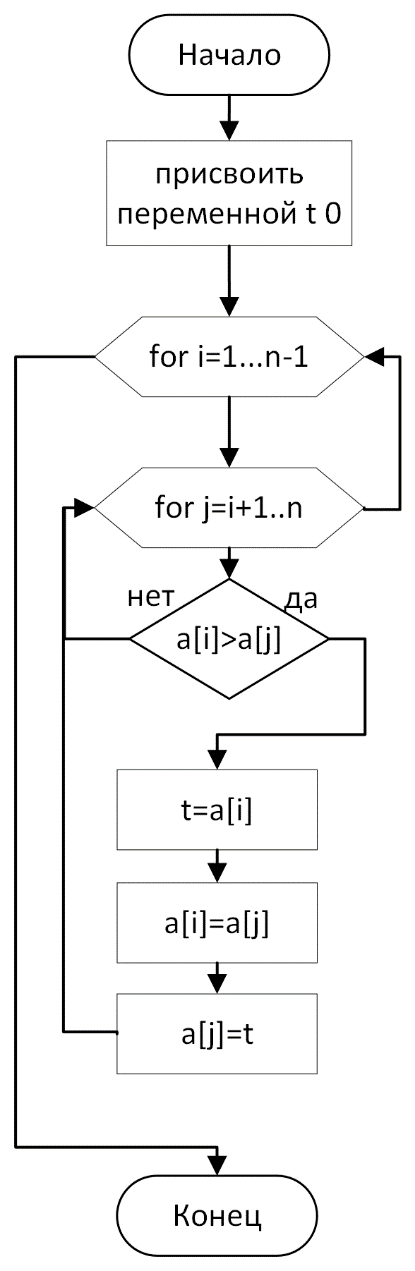
Рисунок 25 – блок-схема алгоритма сортировки
Реализация алгоритма
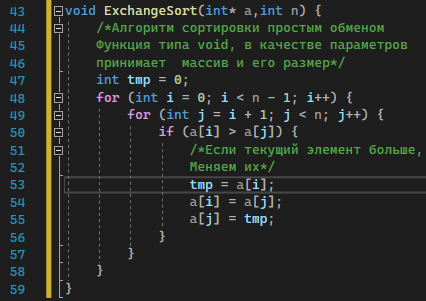

Рисунок 26 – Алгоритм сортировки
Тестирование


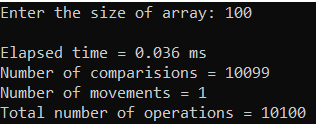
Рисунок 28 – Тестирование при n = 100. Лучший случай
Рисунок 27 – Тестирование и отладка при n = 10.
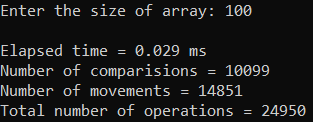





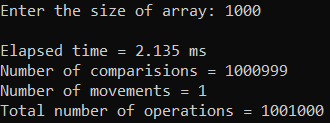
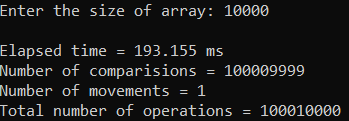
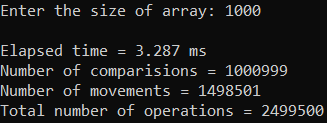
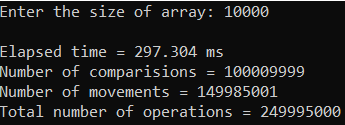
Рисунок 33 – Тестирование при n = 10 000. Худший случай
Рисунок 30 – Тестирование при n = 1000. Лучший случай
Рисунок 29 – Тестирование при n = 100. Худший случай
Рисунок 31 – Тестирование при n = 1000. Худший случай
Рисунок 32 – Тестирование при n = 10 000. Лучший случай
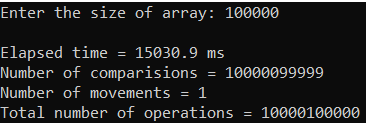

Рисунок 34 – Тестирование при n = 100 000. Лучший случай
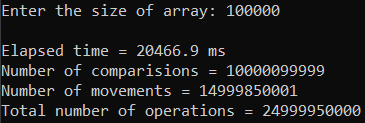

Рисунок 35 – Тестирование при n = 100 000. Худший случай
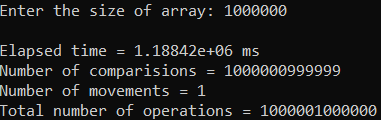


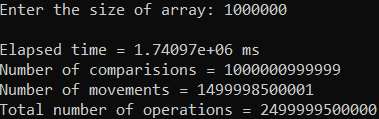
Рисунок 37 – Тестирование при n = 1 000 000. Худший случай
Рисунок 36 – Тестирование при n = 1 000 000. Лучший случай
Обработка результатов
Таблица 4 – Exchange Sort, лучший случай
| n | T(n), мс | Тп(n) = Cф + Mф |
| 100 | 0,036 | 10 100 |
| 1000 | 2,135 | 1 001 000 |
| 10 000 | 193,155 | 100 010 000 |
| 100 000 | 15 030,900 | 10 000 100 000 |
| 1 000 000 | 1 188 420,000 | 1 000 001 000 000 |
Таблица 5 – Exchange Sort, худший случай
| n | T(n), мс | Тп(n) = Cф + Mф |
| 100 | 0,029 | 24 950 |
| 1000 | 3,287 | 2 499 500 |
| 10 000 | 297,304 | 249 995 000 |
| 100 000 | 20 466,900 | 24 999 950 000 |
| 1 000 000 | 1 740 970,000 | 2 499 999 500 000 |
Оценка емкостной сложности
Используется 1 вспомогательная переменная, необходимая для перестановок. Емкостная сложность:
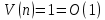
Графики зависимости сложности от n
Г
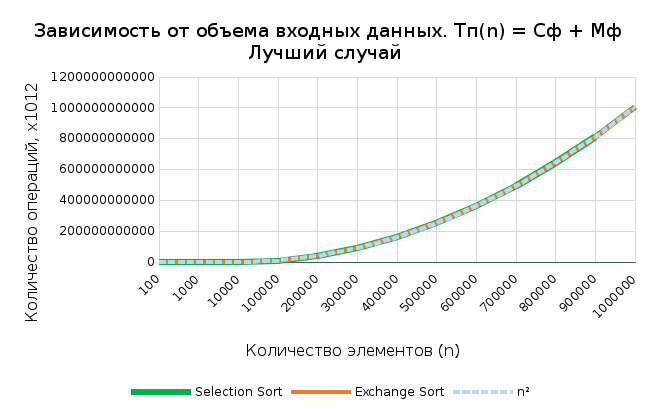 рафик 4
рафик 4Г
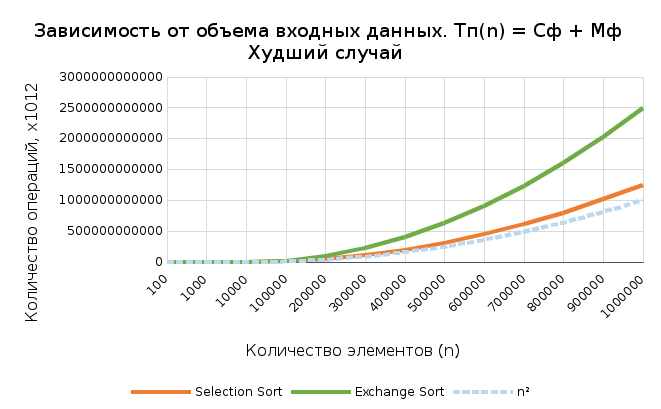 рафик 5
рафик 5Вывод по заданию 3
Полученные данные подтверждают, что оба алгоритма обладают квадратичной вычислительной сложностью, но на основе теоретического расчета можно установить, что функция роста второго алгоритма растет быстрее. Основываясь на графиках и таблицах, можно утверждать, что время выполнения зависит и от исходного состояния массива. Наибольшая разница заметна при худшем случае, в то время как сложности в лучшем и среднем случаях практически совпадают. Емкостная сложность у обоих алгоритмов – константная.
Вывод
В ходе работы приобретены и отработаны практические навыки по:
определению сложности алгоритмов сортировки на теоретическом и практическом уровнях;
определению емкостной сложности алгоритмов сортировки;
реализацией алгоритмов сортировки;
определению зависимости (квадратичной/линейной) сложности алгоритма сортировки от объема входных данных;
нахождению оптимального алгоритма сортировки с помощью данных, полученных в ходе теоретического расчета и практического выполнения.

 Вывод по заданию 1
Вывод по заданию 1