отчет по практической. Отчет по практической работе 6 Построение комбинационных схем, реализующих мднф и мкнф заданной логической функции от 4х переменных в базисах
 Скачать 477.6 Kb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет» РТУ МИРЭА  Институт искусственного интеллекта Кафедра общей информатики ОТЧЕТПО ПРАКТИЧЕСКОЙ РАБОТЕ № 6 Построение комбинационных схем, реализующих МДНФ и МКНФ заданной логической функции от 4-х переменных в базисахИ-НЕ, ИЛИ-НЕ.по дисциплине«ИНФОРМАТИКА» Выполнил студент группы ИКБО-09-22Федченко Д.А. Принял Смирнов С.С Старший преподаватель кафедры ОИ
Москва 2022 СОДЕРЖАНИЕ ОТЧЕТ 1 Построение комбинационных схем, реализующих МДНФ и МКНФ заданной логической функции от 4-х переменных в базисах 1 И-НЕ, ИЛИ-НЕ. 1 по дисциплине 1 1ПОСТАНОВКА ЗАДАЧИ И ПЕРСОНАЛЬНЫЙ ВАРИАНТ 5 2ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 6 2.1 Восстановление таблицы истинности 6 A 6 B 6 C 6 D 6 F 6 0 6 0 6 0 6 0 6 1 6 0 6 0 6 0 6 1 6 1 6 0 6 0 6 1 6 0 6 1 6 0 6 0 6 1 6 1 6 1 6 0 6 1 6 0 6 0 6 1 6 0 6 1 6 0 6 1 6 0 6 0 6 1 6 1 6 0 6 0 6 0 6 1 6 1 6 1 6 1 6 1 6 0 6 0 6 0 6 0 6 1 6 0 6 0 6 1 6 0 6 1 6 0 6 1 6 0 6 1 6 1 6 0 6 1 6 1 6 0 6 1 6 1 6 0 6 0 6 1 6 1 6 1 6 0 6 1 6 1 6 1 6 1 6 1 6 0 6 0 6 1 6 1 6 1 6 1 6 1 6 6 Таблица 1 - Таблица истинности для функции F 6 2.2 Минимизация логической функции при помощи карт Карно 7 2.3 Приведение МДНФ и МКНФ к базисам «И-НЕ» и «ИЛИ-НЕ» 9 2.4 Схемы, реализующие МДНФ и МКНФ в требуемых 9 логических базисах 9 3ВЫВОДЫ 13 4ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 14 1.Информатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов – М., МИРЭА – Российский Технологический Университет, 2020,- 102 с. 14 2.Cburch: справочная система по программе “Logisism”: сайт – URL: http://www.cburch.com/logisism/docs/2.5/ru/ 14 1 ПОСТАНОВКА ЗАДАЧИ И ПЕРСОНАЛЬНЫЙ ВАРИАНТ 3 2 ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4 2.1 Восстановление таблицы истинности 4 2.2 Минимизация логической функции при помощи карт Карно 5 2.3 Приведение МДНФ и МКНФ к базисам «И-НЕ» и «ИЛИ-НЕ» 7 2.4 Схемы, реализующие МДНФ и МКНФ в требуемых логических базисах 8 3 ВЫВОДЫ 11 4 ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 12 ПОСТАНОВКА ЗАДАЧИ И ПЕРСОНАЛЬНЫЙ ВАРИАНТЛогическая функция от четырех переменных задана в 16-теричной векторной форме: F (a, b, c, c) = F92D16. Восстановить таблицу истинности. Минимизировать логическую функцию при помощи карт Карно и получить формулы МДНФ и МКНФ в общем базисе. Перевести МДНФ и МКНФ в базисы «И-НЕ» и «ИЛИ-НЕ» (каждую минимальную форму в два базиса). Построить комбинационные схемы для приведенных к базисам формул МДНФ и МКНФ в лабораторном комплексе, используя только логические элементы, входящие в конкретный базис. Протестировать работу схем и убедиться в их правильности. Подготовить отчет о проделанной работе и защитить ее 2.1 Восстановление таблицы истинностиВ соответствии с вариантом функция, заданная в 16-теричной форме имеет следующий вид: F (a, b, c, d) = F92D16 Преобразуем ее в двоичную запись: 1111 1001 0010 11012 – получили столбец значений логической функции, который необходим для восстановления полной таблицы истинности (смотри табл.1)
Таблица 1 - Таблица истинности для функции F2.2 Минимизация логической функции при помощи карт Карно     Д  алее построим МДНФ заданной функции. Для этого воспользуемся методом карт Карно и сразу же выделим интервалы, на которых функция сохраняет свое единичное значение. Разместим единичные значения функции на карте Карно, предназначенной для минимизации функции от четырех переменных (рисунок 1). Напоминаем, что местоположение значения функции на карте в каждом конкретном случае определяется координатами, которые представляют собой комбинацию значений переменных.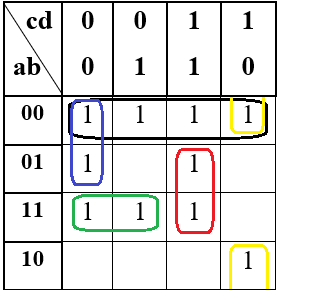 Рисунок 1 - Карта Карно, заполненная для построения МДНФ с интервалами. Далее запишем формулу МДНФ, для чего последовательно рассмотрим каждый из интервалов. Для каждого интервала запишем минимальную конъюнкцию, куда будут входить только те переменные и их отрицания, которые сохраняют свое значение на этом интервале. Переменные, которые меняют свое значение на интервале, упростятся. Чтобы получить МДНФ остается только объединить при помощи дизъюнкции имеющееся множество минимальных конъюнкций. Получаем формулу для всей МДНФ (см. формулу 1). FМДНФ = 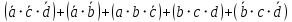 (1)По заданию также требуется построить МКНФ рассматриваемой функции и тоже выразить ее в разных базисах. МКНФ строится по нулевым значениям логической функции. Обратимся еще раз к карте Карно для нашей таблицы и изменим его: на пустых клетках поставим нулевые значения, а единичные значения удалим для повышения наглядности рисунка. Интервалы выделим сразу. Получится карта, показанная на рисунке 2. 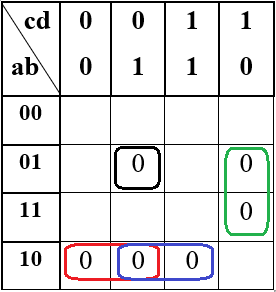     Рисунок 2 - Карта Карно, заполненная для построения МКНФ с интервалами. Запишем формулу МКНФ, для чего последовательно рассмотрим каждый из интервалов. Для каждого интервала запишем минимальную дизъюнкцию, куда будут входить только те переменные и их отрицания, которые сохраняют свое значение на этом интервале. Переменные, которые меняют свое значение на интервале, упростятся. Чтобы получить МКНФ, необходимо объединить при помощи конъюнкции множество минимальных дизъюнкций, построенных для всех имеющихся интервалов (см. формулу 2). FMКНФ = 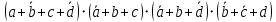 (2)2.3 Приведение МДНФ и МКНФ к базисам «И-НЕ» и «ИЛИ-НЕ»Теперь приведем полученные МДНФ (см. формулу 1) к базисам «И-НЕ» и «ИЛИ-НЕ». Для этого воспользуемся законами де Моргана, в результате получим формулы (3, 4). FМДНФи-не = 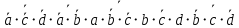 (3)FМДНФили-не = 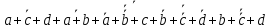 (4)Теперь приведем полученные МКНФ (см. формулу 2) к базисам «И-НЕ» и «ИЛИ-НЕ». Для этого воспользуемся законами де Моргана, в результате получим формулы (5, 6). FMКНФи-не = 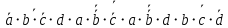 (5)FMКНФили-не = 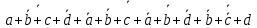 (6) 2.4 Схемы, реализующие МДНФ и МКНФ в требуемыхлогических базисахПостроим в лабораторном комплексе комбинационные схемы, реализующие рассматриваемую функцию в базисах «И-НЕ» и «ИЛИ-НЕ» (всего 4 схемы), протестируем их работу и убедимся в их правильности (рис. 3 – 6). 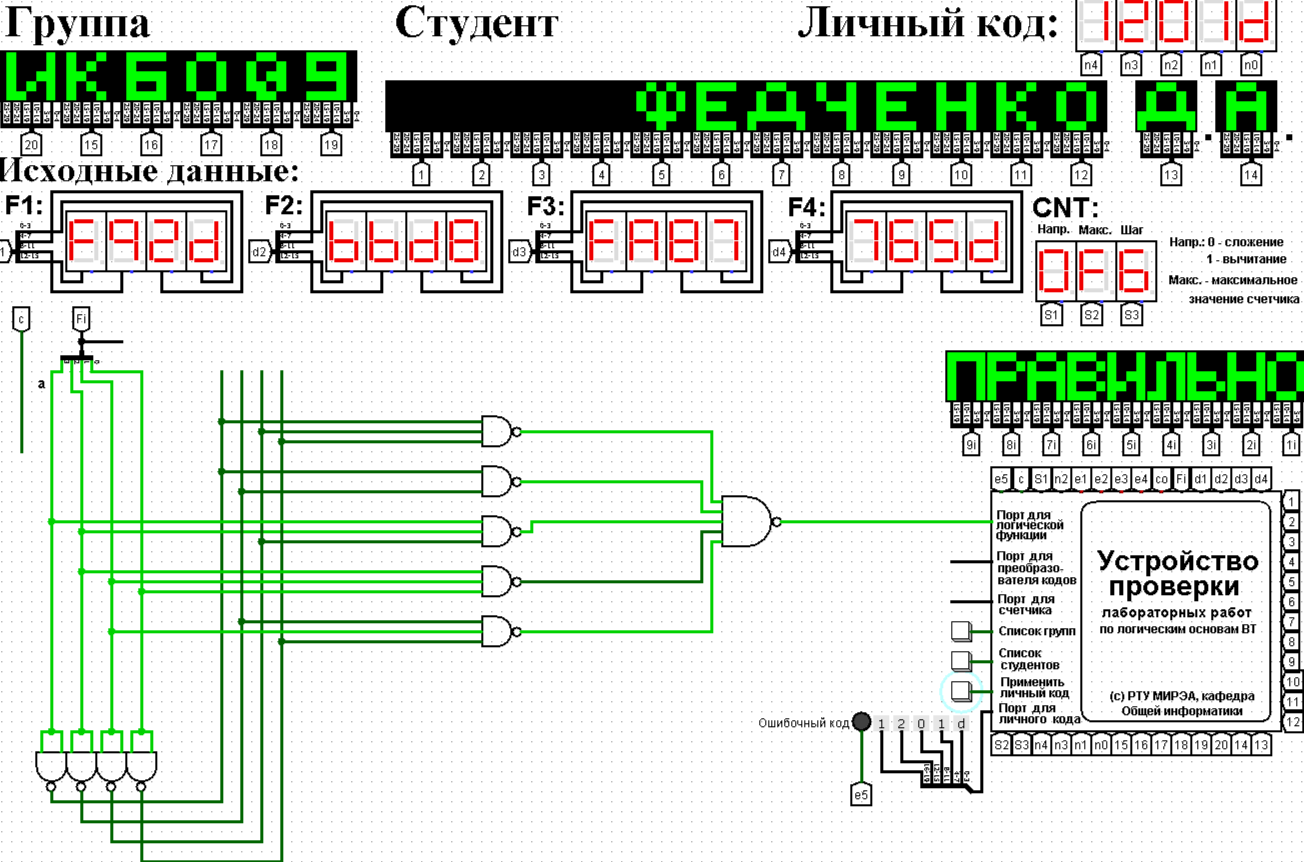 Рисунок 3 - Тестирование схемы МДНФ, построенной в базисе «И-НЕ» 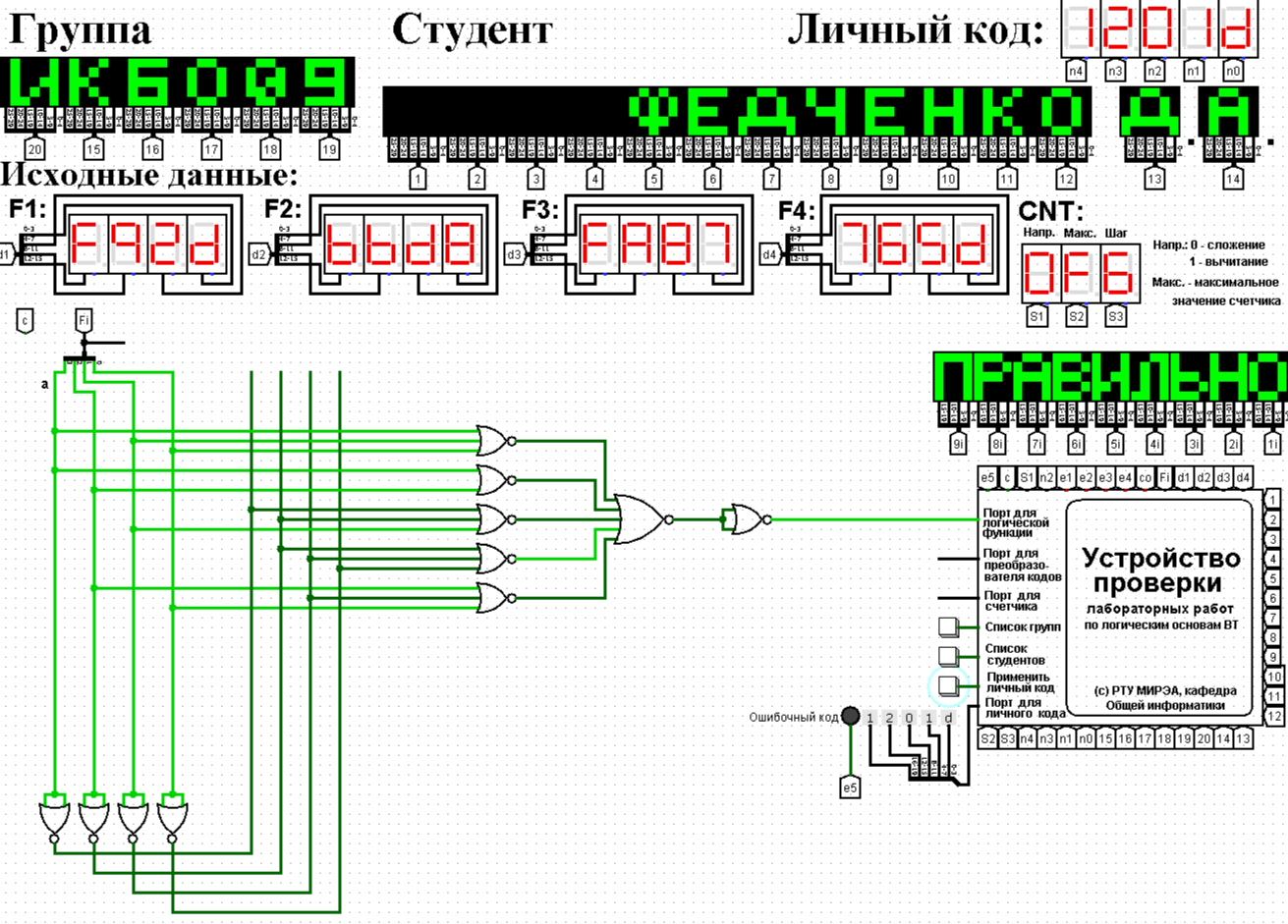 Рисунок 4 - Тестирование схемы МДНФ, построенной в базисе «ИЛИ-НЕ» 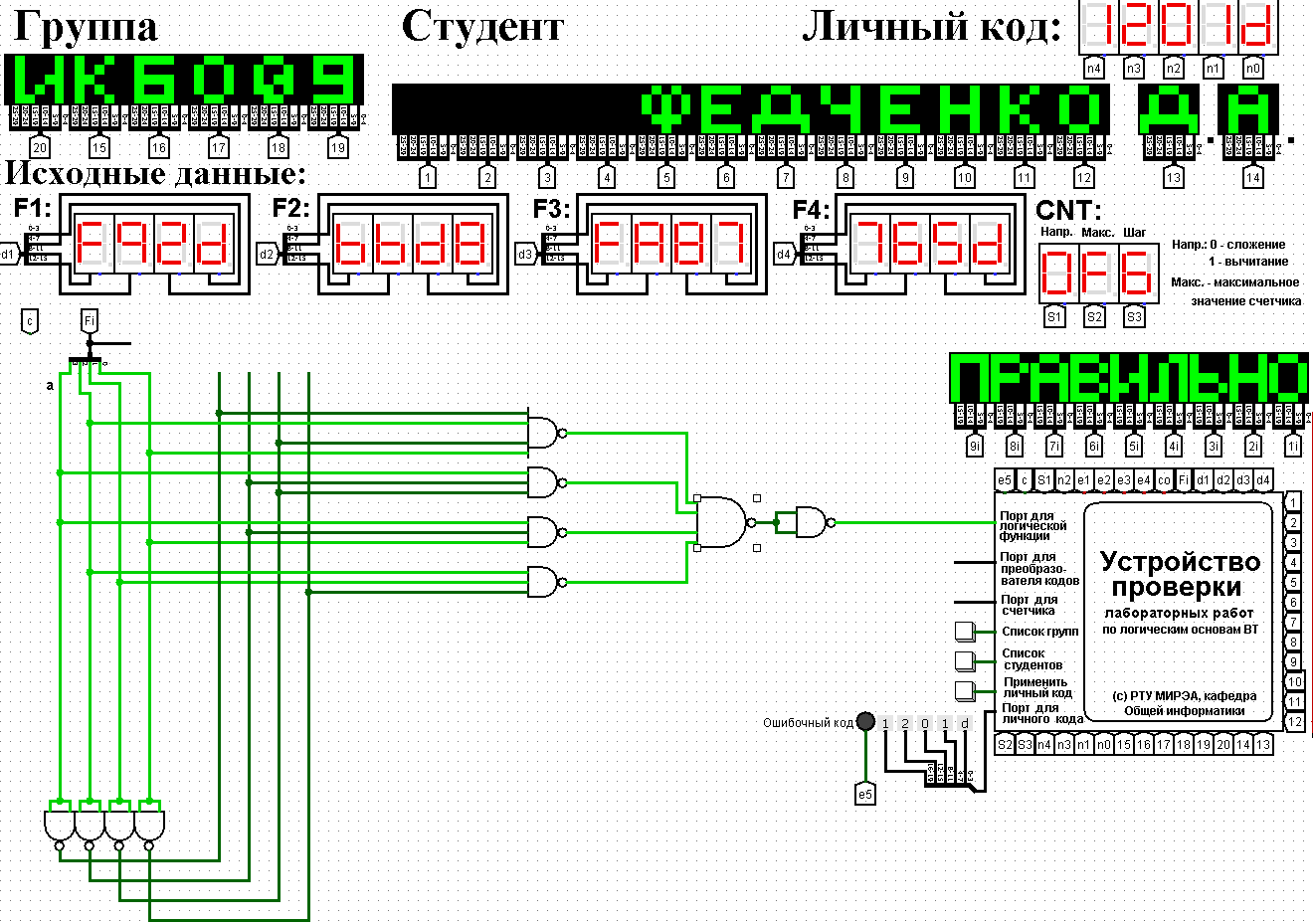 Рисунок 5 - Тестирование схемы МКНФ, построенной в базисе «И-НЕ» 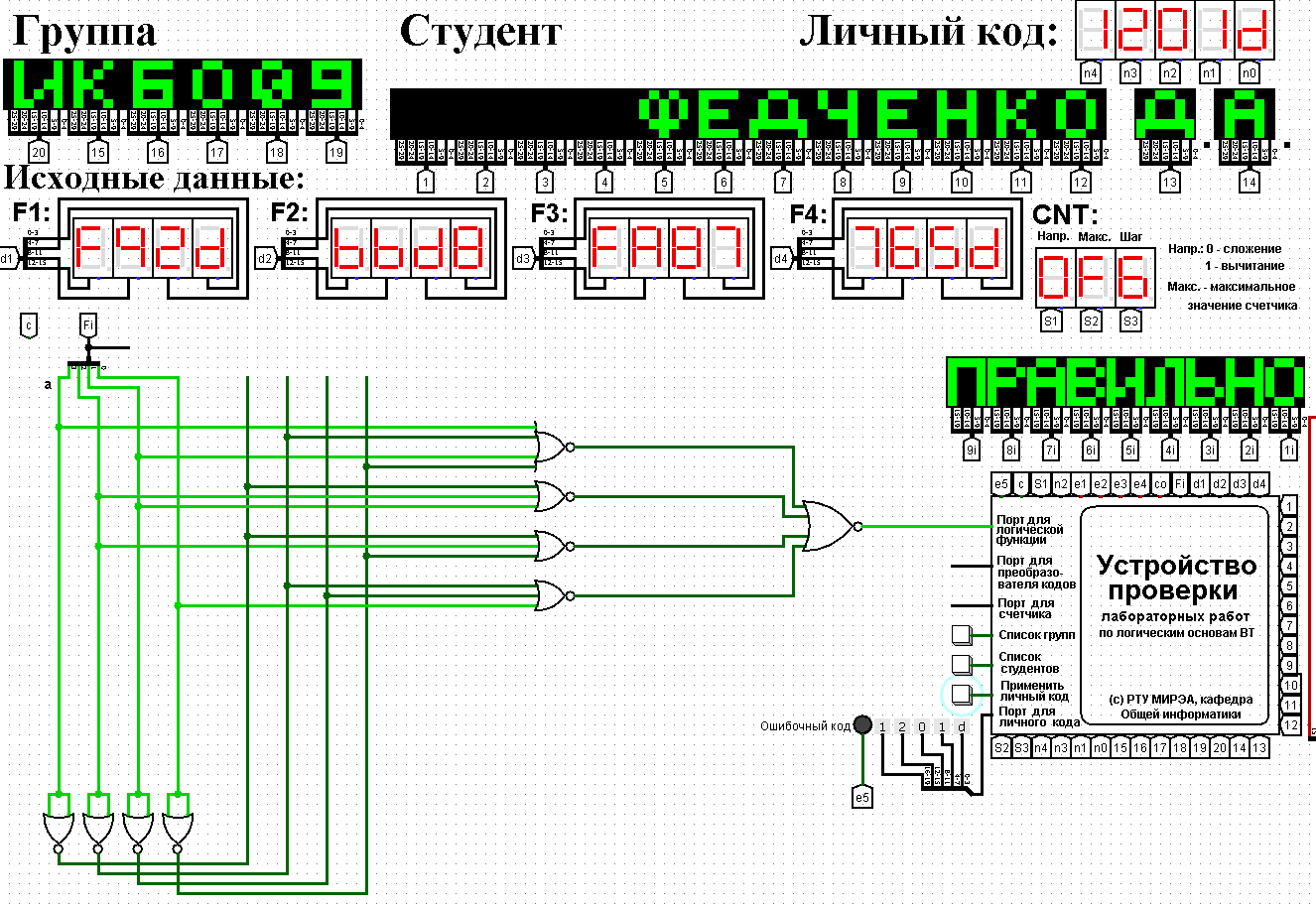 Рисунок 6 - Тестирование схемы МКНФ, построенной в базисе «ИЛИ-НЕ» Тестирование показало, что все схемы работают правильно. ВЫВОДЫТаблицы истинности восстановлены. Функция минимизирована при помощи карт Карно и получены формулы МДНФ и МНКФ. Формулы переведены в базис «И-НЕ» и «ИЛИ-НЕ». Комбинационные схемы МДНФ и МКНФ для обоих базисов построены в лабораторном комплексе. Работа схем протестирована и проверена на правильность. ИНФОРМАЦИОННЫЕ ИСТОЧНИКИИнформатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов – М., МИРЭА – Российский Технологический Университет, 2020,- 102 с.Cburch: справочная система по программе “Logisism”: сайт – URL: http://www.cburch.com/logisism/docs/2.5/ru/ |