Главная страница
Навигация по странице:

  • «МИРЭА

  • Восстановленная таблица истинности

  • Реализация логической функции на дешифраторах 4-16, 3-8, 2-4.

    		•

    отчет 7. Отчет по практической работе 7 Реализация заданной логической функции от четырех переменных на дешифраторах 416, 38 и 24 по дисциплине


    Скачать 495.49 Kb.
    НазваниеОтчет по практической работе 7 Реализация заданной логической функции от четырех переменных на дешифраторах 416, 38 и 24 по дисциплине
    Анкоротчет 7
    Дата13.11.2022
    Размер495.49 Kb.
    Формат файлаdocx
    Имя файлаPRAKTIKA7.docx
    ТипОтчет
    #786205




    МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

    Федеральное государственное бюджетное образовательное учреждение высшего

    образования

    «МИРЭА - Российский технологический университет»
    РТУ МИРЭА




    Институт искусственного интеллекта

    Кафедра общей информатики


    ОТЧЕТ


    ПО ПРАКТИЧЕСКОЙ РАБОТЕ № 7

    Реализация заданной логической функции от четырех переменных на дешифраторах 4-16, 3-8 и 2-4

    по дисциплине


    «ИНФОРМАТИКА»

    Выполнил студент группы ИВБО-04-22 Гумеров А.Р.

    Принял Корчемная А.И.

    Ассистент

    Практическая
    «11» ноября 2022 г.
    __________________

    работа выполнена






    «Зачтено»
    «»2022 г.
    __________________

    СОДЕРЖАНИЕ

    ОТЧЕТ 1

    по дисциплине 1

    1ПОСТАНОВКА ЗАДАЧИ 3

    2ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4

    2.1Восстановленная таблица истинности 4

    2.2Реализация логической функции на дешифраторах 4-16, 3-8, 2-4. 5

    3ВЫВОДЫ 10

    4ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 11

    1 ПОСТАНОВКА ЗАДАЧИ 3

    2 ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4

    2.1 Восстановленная таблица истинности 4

    2.2 Реализация логической функции на дешифраторах 4-16, 3-8, 2-4 5

    3 ВЫВОДЫ 10

    4 ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 11


    1. ПОСТАНОВКА ЗАДАЧИ


    Логическая функция от четырёх переменных задана в 16-теричной

    векторной форме. Восстановить таблицу истинности. По таблице истинности реализовать в лабораторном комплексе логическую функцию на дешифраторах тремя способами:

    – используя дешифратор 4-16 и одну дополнительную схему «или»;

    – используя два дешифратора 3-8 и необходимую дополнительную логику;

    – используя пять дешифраторов 2-4 и одну дополнительную схему «или».

    Протестировать работу схем и убедиться в правильности их работы.

    Подготовить отчет о проделанной работе и защитить ее.

    1. ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ

      1. Восстановленная таблица истинности


    В соответствии с вариантом функция, заданная в 16-теричной форме имеет следующий вид:

    F (a, b, c, d) = Cd7316

    Преобразовав данную логическую функцию в двоичную запись: 1100 1101 0111 00112 – получается столбец значений логической функции, который необходим для восстановления полной таблицы истинности (см. табл. 1)

    Таблица 1 – таблица истинности для функции F

    a
    b
    c
    d
    F

    0
    0
    0
    0
    1

    0
    0
    0
    1
    1

    0
    0
    1
    0
    0

    0
    0
    1
    1
    0

    0
    1
    0
    0
    1

    0
    1
    0
    1
    1

    0
    1
    1
    0
    0

    0
    1
    1
    1
    1

    1
    0
    0
    0
    0

    1
    0
    0
    1
    1

    1
    0
    1
    0
    1

    1
    0
    1
    1
    1

    1
    1
    0
    0
    0

    1
    1
    0
    1
    0

    1
    1
    1
    0
    1

    1
    1
    1
    1
    1

      1. Реализация логической функции на дешифраторах 4-16, 3-8, 2-4.


    Реализуем функцию, используя дешифратор 4-16 и одну дополнительную схему «или». Количество выходов дешифратора соответствует количеству значений логической функции, поэтому требуется только один такой дешифратор. Подадим значения переменных функции на адресные входы дешифратора: младшую переменную «d» - на младший адресный вход, старшую переменную «a» - на старший адресный вход, прочие переменные –аналогично. В процессе работы на выходах дешифратора будут последовательно возникать единичные значения в соответствии с поступающей на адресные входы комбинацией значений переменных. Выберем лишь те выходы дешифратора, номера которых совпадают с номерами наборов значений переменных, на которых функция равна единице. Объединим эти выходы дешифратора через «или» и получим требуемую реализацию (рис.1).

    Сразу после добавления дешифратора на рабочую область настраиваем ему некоторые свойства:

    – «выбирающие биты» (адресные входы) устанавливаем равными 4;

    – «три состояния» — нет;

    – «на отключенном выходе» — устанавливаем равным 0;

    – «разрешающий вход» — нет.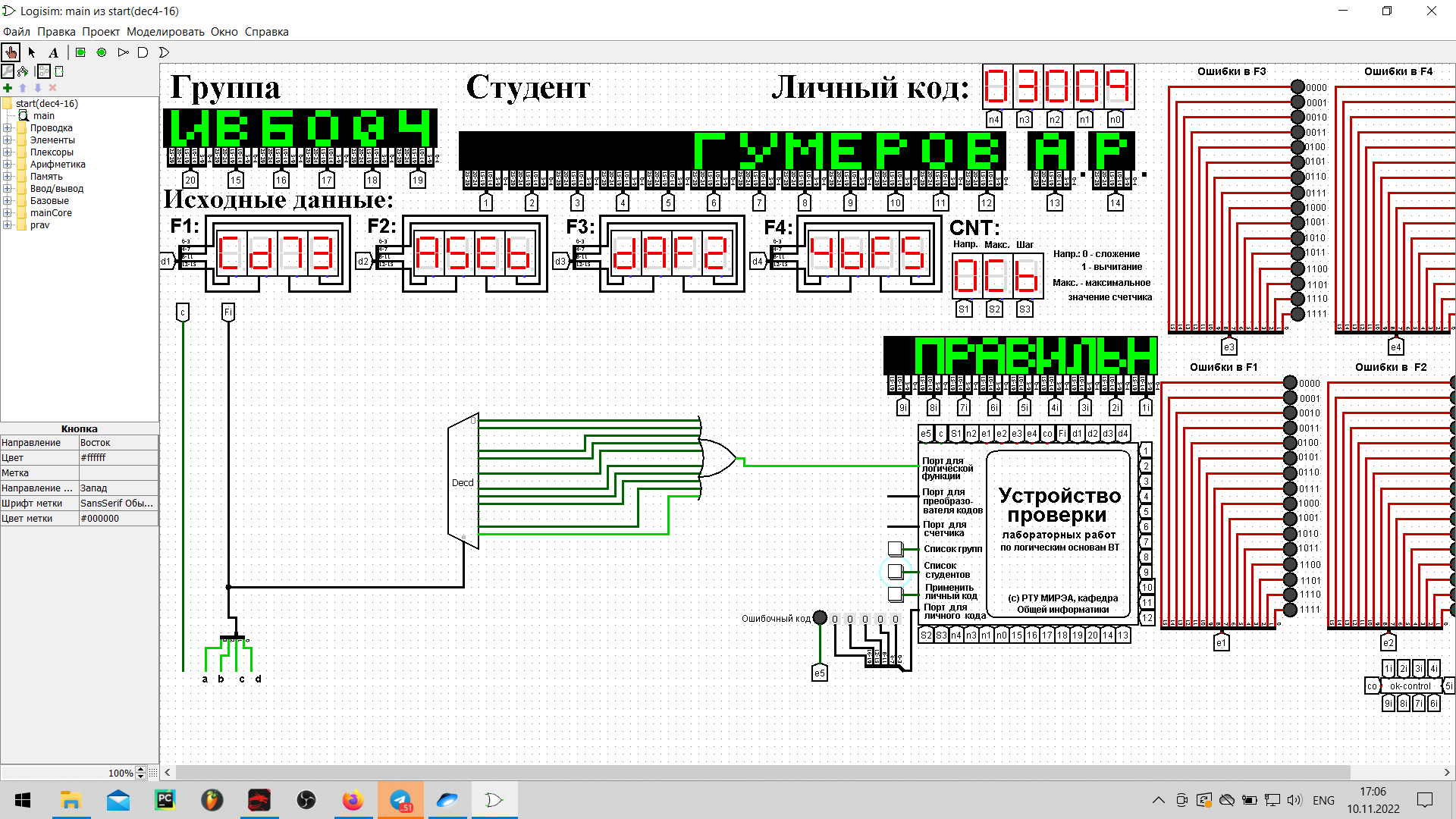



    Рисунок 1 – Тестирование схемы, реализующей логическую функцию на дешифраторе 4-16

    Тестирование показало, что схема работает правильно.

    Реализуем функцию, используя дешифраторы 3-8 и необходимую дополнительную логику. Количество выходов у дешифратора 3-8 в два раза меньше количества значений логической функции, поэтому потребуется разместить на рабочей области лабораторного комплекса два дешифратора 3-8. Также следует обратить внимание, что количество адресных входов дешифратора меньше, чем количество переменных функции. Поэтому подадим значения трех младших переменных функции на адресные входы обоих дешифраторов: младшую переменную «d» — на младший адресный вход, старшую переменную «b» — на старший адресный вход, переменную «с» — аналогично. Переменная «а» используется для управления дешифраторами. Когда «а» равна нулю, то должен работать первый дешифратор - он отвечает за первую половину таблицы истинности. Когда «а» равна единице, то должен работать второй дешифратор — он отвечает за вторую половину таблицы истинности. Чтобы это реализовать, переменная «а» должна подаваться на разрешающий вход первого дешифратора через инверсию, а на вход второго — без инверсии.

    Для того чтобы у дешифраторов появился разрешающий вход, потребуется в их свойствах активировать соответствующую опцию. Прочие настройки дешифраторов оставляем аналогичными предыдущей реализации. В процессе работы на выходах всех дешифраторов будут последовательно возникать единичные значения в соответствии с поступающей на адресные входы комбинацией значений переменных. У первого дешифратора выберем лишь те выходы, чьи номера совпадают с номерами наборов значений переменных, на которых функция равна единице, из первой половины таблицы. У второго дешифратора выберем лишь те выходы, чьи номера совпадают с номерами наборов значений переменных за вычетом 8, на которых функция равна единице, из второй половины таблицы. Объединим выбранные выходы обоих дешифраторов через «или» и получим требуемую реализацию (рис.2).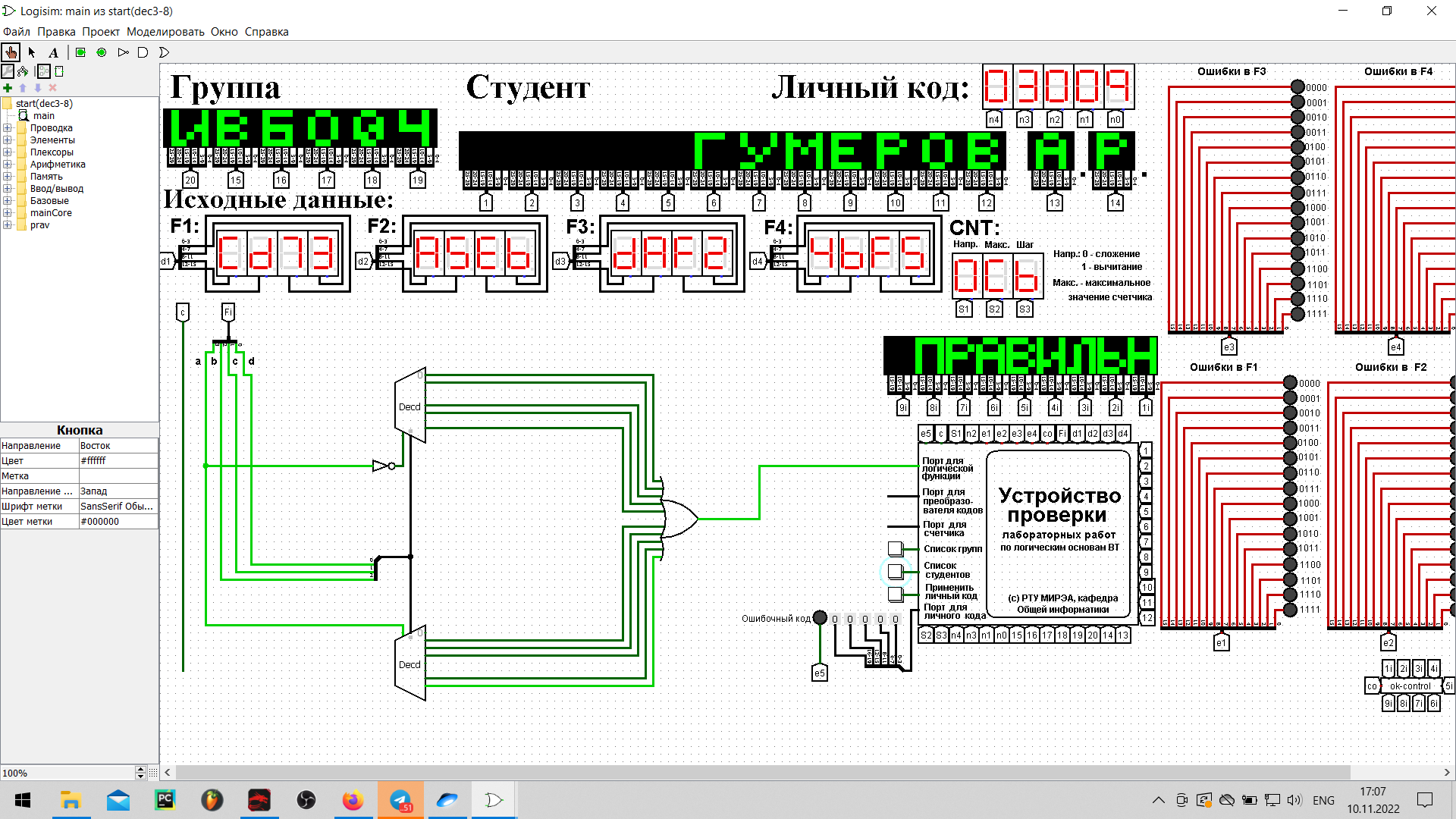



    Рисунок 2 – Тестирование схемы, реализующей логическую функцию на дешифраторах 3-8 и дополнительной логике

    Тестирование подтвердило правильность работы схемы.

    Реализуем функцию, используя дешифраторы 2-4 и необходимую дополнительную логику. Количество выходов у дешифратора 2-4 в четыре раза меньше количества значений логической функции, поэтому потребуется разместить на рабочей области лабораторного комплекса четыре дешифратора 2-4, которые будут называться операционными, а также еще один дешифратор 2-4, который будет управлять первыми четырьмя – управляющий. Итого всего потребуется пять дешифраторов 2-4 и дополнительная схема «или». Следует обратить внимание, что количество адресных входов у каждого дешифратора в два раза меньше, чем количество переменных функции, поэтому каждый операционный дешифратор будет отвечать лишь за одну четверть исходной таблицы истинности.

    Значения двух младших переменных функции используются для адресации четырех операционных дешифраторов: младшая переменная «d» - подается на младший адресный вход, старшая переменная «с» - на старший адресный вход (на схеме далее переменные подаются на адресные входы дешифраторов при помощи разветвителя и шины). Переменные «а» и «b» используется для управления операционными дешифраторами и аналогичным образом подаются на адресные входы управляющего дешифратора. Выходы управляющего дешифратора должны быть подключены к разрешающим входам операционных дешифраторов. Таким образом, когда «а» и «b» равны нулю, то на нулевом выходе управляющего дешифратора образуется единица, которая подается на разрешающий вход первого операционного дешифратора. И так далее, аналогично. Теперь фактически каждый операционный дешифратор отвечает за свою двоичную тетраду в исходной векторной записи логической функции. Выберем у каждого операционного дешифратора лишь те выходы, где у двоичной тетрады стоят единицы. При этом необходимо считать, что нулевой выход соответствует старшему двоичному разряду тетрады. Объединим выбранные выходы всех операционных дешифраторов через «или» и получим требуемую реализацию (рис.3).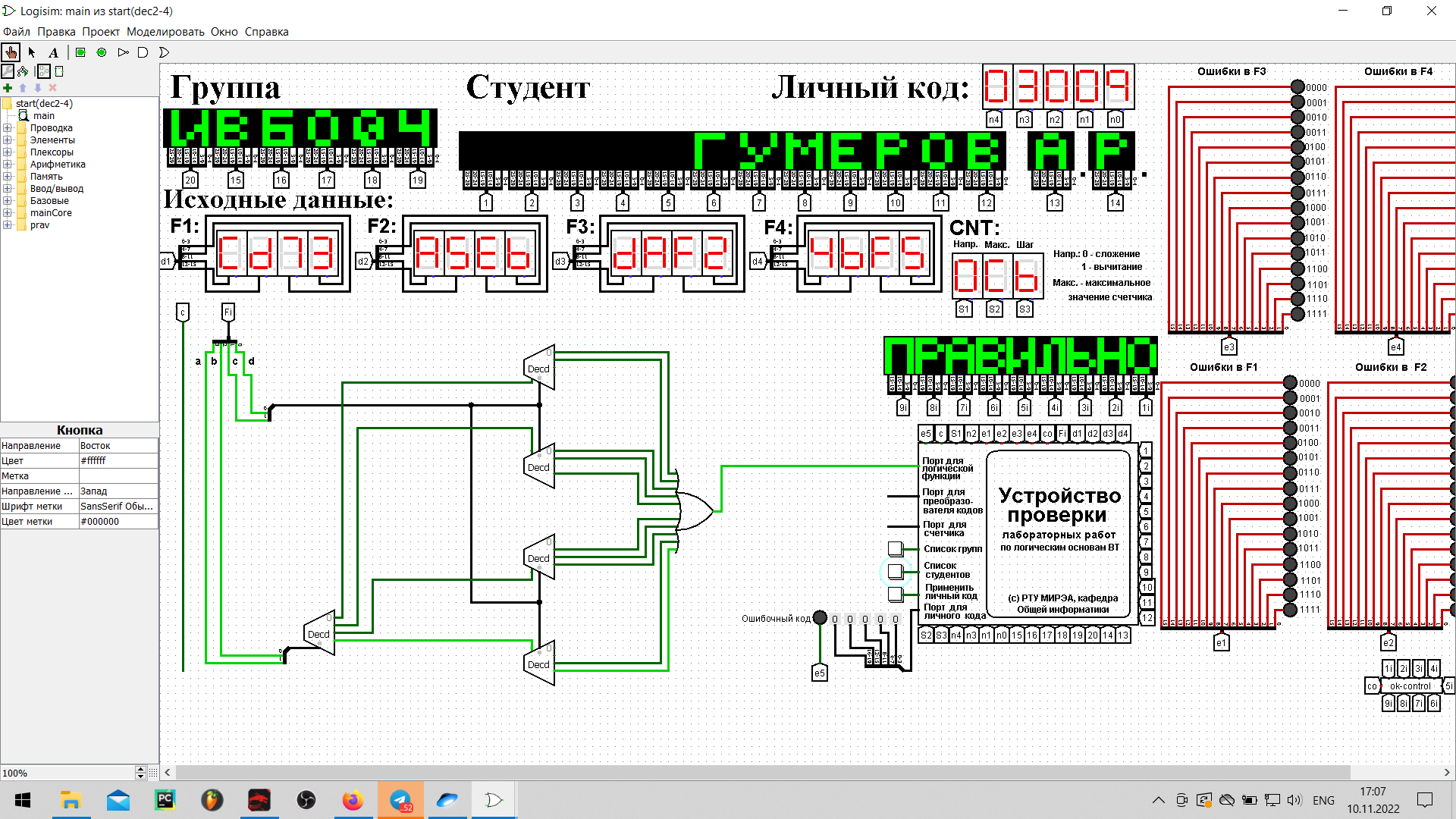



    Рисунок 3 – Тестирование схемы, реализующей логическую функцию на дешифраторах 2-4 и дополнительной логике

    Тестирование подтвердило правильность работы схемы.

    1. ВЫВОДЫ


    По данной логической функции от четырех переменных, заданной в 16-теричной векторной форме, была восстановлена таблица истинности. По таблице истинности логическая функция реализована в лабораторном комплексе на дешифраторах тремя способами:

    – используя дешифратор 4-16 и одну дополнительную схему «или»;

    – используя два дешифратора 3-8 и необходимую дополнительную логику;

    – используя пять дешифраторов 2-4 и одну дополнительную схему «или».

    Протестирована работа схем и их правильность.

    1. ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ


    1. Информатика: Методические указания по выполнению практических и лабораторных работ / С.С. Смирнов, Д.А. Карпов; Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет». – Москва: РТУ МИРЭА, 2020. – 102 с. – Текст: непосредственный.

    2. Лекции по информатике. Г.Б. Воронов — Москва: РТУ МИРЭА, 2022





    Москва 2022

    написать администратору сайта