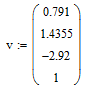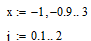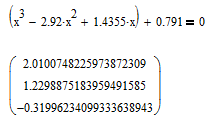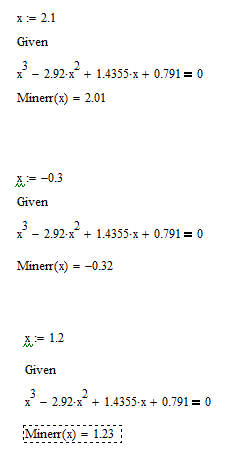|
|
1 раб. Отчет по практике Вариант 1 Нахождение корней уравнения в MathCad студентка группы итс11
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Поволжский государственный технологический университет
Кафедра радиотехники и связи
Отчет по практике
Вариант № 1
Нахождение корней уравнения в MathCad
Выполнила: студентка группы ИТС-11
Блинова Е.В.
Проверил: аспирант кафедры РТиС
Чернов А.А.
Йошкар-Ола
2010
Цель работы: нахождение корней уравнения в программе MathCad с использованием встроенных функций root, polyroots, символьного решения.
№ варианта
|
Интервал нахождения корней
|
Уравнение
|
1
|
[-1; 3]
|
x3-2,92x2+1,4355x+0,791=0
|
І
Запускаем программу MathCad
Записываем функцию f(x)= x3-2,92x2+1,4355x+0,791
Интервал для нахождения корней определяется шагом в 0.1 т.е. 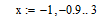
Строим график функции f(x)= x3-2,92x2+1,4355x+0,791 и x0=0. Форматируем график. Нажимаем на пустом месте в поле графика, вызываем контекстное меню (пкм) во вкладке «Формат» ставим галочку в поле «Линии сетки» и «Стиль осей: пересекающиеся»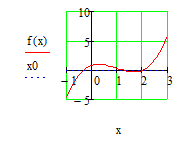
Далее, на графике определяем точки пересечения кривой заданной функцией f(x) и х0. Мы видим, что таких точек всего 3. Точное значение х1, х2, х3 мы сможем узнать вызвав контекстное меню в поле «Трассировка». Получим значения: -0.3; 1.2;2.1 соответственно.
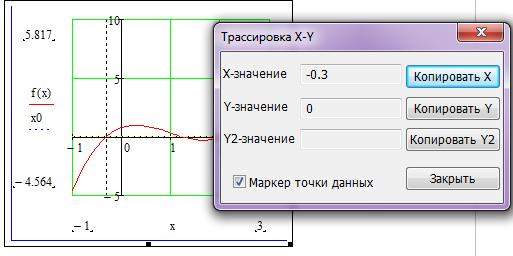
Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3)

II
Найдем корни заданного в варианте уравнения вторым способом.
Создаем вектор из коэффициентов уравнения, используя панель управления Матрица. Задав один столбец и четыре строки для коэффициентов уравнения.
Вектор из коэффициентов уравнения будет иметь следующий вид
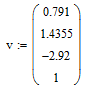
С помощью встроенной функции r:=polyroots(v) найдем корни уравнения и представим их в виде вектора rT, транспонированного по отношению к r, то есть преобразованного из столбца в строку.

Создаем циклы для переменной х и количества найденных корней:
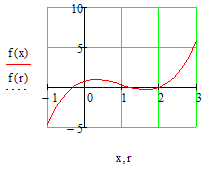
Строим график для функции f(x) и f(r)
III
Найдем корни уравнения 3 способом.
Приравниваем левую часть уравнения к нулю с помощью логического знака «=» (Ctrl+=)
Выделяем переменную х и в главном меню выбираем Символика/Переменная/Решить
Найдены корни уравнения запишутся в виде вектора:
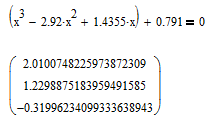
IV
4 способ нахождения приближенного значения решения уравнения использованием функции minerr( x1,…).
Записываем чему равно х.
Вводим ключевое слово given (дано), с которого начинается блок решений.
Записывем уравнение, используя знак логического равенства между правой и левой частью уравнения.
Обращаемся к функции minerr( x). Корень будет найден.
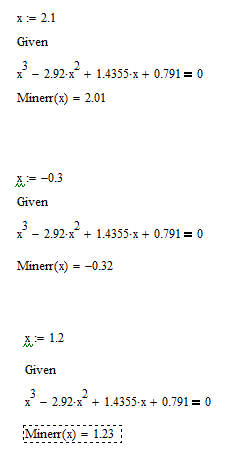 |
|
|
 Скачать 84.13 Kb.
Скачать 84.13 Kb.