УП03. ГАПОУ ПК 8. Верещагин1 УП03. 33ОБАс. Отчет по учебной практике уп 03. Защита информации техническими средствами

Название	Отчет по учебной практике уп 03. Защита информации техническими средствами
Анкор	УП03. ГАПОУ ПК 8
Дата	06.12.2022
Размер	120.97 Kb.
Формат файла
Имя файла	Верещагин1 УП03. 33ОБАс.docx
Тип	Отчет #831753
страница	4 из 4

1 2 3 4

Глава 3. Описание алгоритмов реализации функции хеширования.

Существует множество алгоритмов хеширования, отличающихся различными свойствами. Примеры свойств:

разрядность;
вычислительная сложность;
криптостойкость.

Принято считать, что хорошей, с точки зрения практического применения, является такая хеш-функция, которая удовлетворяет следующим условиям:

функция должна быть простой с вычислительной точки зрения;
функция должна распределять ключи в хеш-таблице наиболее равномерно;
функция не должна отображать какую-либо связь между значениями ключей в связь между значениями адресов;
функция должна минимизировать число коллизий – то есть ситуаций, когда разным ключам соответствует одно значение хеш-функции (ключи в этом случае называются синонимами ).

При этом первое свойство хорошей хеш-функции зависит от характеристик компьютера, а второе – от значений данных.

Если бы все данные были случайными, то хеш-функции были бы очень простые (например, несколько битов ключа). Однако на практике случайные данные встречаются достаточно редко, и приходится создавать функцию, которая зависела бы от всего ключа. Если хеш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то хеширование эффективно разбивает множество ключей. Наихудший случай – когда все ключи хешируются в один индекс.

При возникновении коллизий необходимо найти новое место для хранения ключей, претендующих на одну и ту же ячейку хеш-таблицы. Причем, если коллизии допускаются, то их количество необходимо минимизировать. В некоторых специальных случаях удается избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую инъективную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.

Хеш-таблицы должны соответствовать следующим свойствам.

Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение является индексом в исходном массиве.
Количество хранимых элементов массива, деленное на число возможных значений хеш-функции, называется коэффициентом заполнения хеш-таблицы ( load factor ) и является важным параметром, от которого зависит среднее время выполнения операций.
Операции поиска, вставки и удаления должны выполняться в среднем за время O(1). Однако при такой оценке не учитываются возможные аппаратные затраты на перестройку индекса хеш-таблицы, связанную с увеличением значения размера массива и добавлением в хеш-таблицу новой пары.
Механизм разрешения коллизий является важной составляющей любой хеш-таблицы.

Хеширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа. Хэш-таблицы часто применяются в базах данных, и, особенно, в языковых процессорах типа компиляторов и ассемблеров, где они повышают скорость обработки таблицы идентификаторов. В качестве использования хеширования в повседневной жизни можно привести примеры распределение книг в библиотеке по тематическим каталогам, упорядочивание в словарях по первым буквам слов, шифрование специальностей в вузах и т.д.

Методы разрешения коллизий

Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют способы преодоления возникающих сложностей:

метод цепочек (внешнее или открытое хеширование);
метод открытой адресации (закрытое хеширование).

Метод цепочек. Технология сцепления элементов состоит в том, что элементы множества, которым соответствует одно и то же хеш-значение, связываются в цепочку-список. В позиции номер i хранится указатель на голову списка тех элементов, у которых хеш-значение ключа равно i ; если таких элементов в множестве нет, в позиции i записан NULL. На рис. 38.1 демонстрируется реализация метода цепочек при разрешении коллизий. На ключ 002 претендуют два значения, которые организуются в линейный список.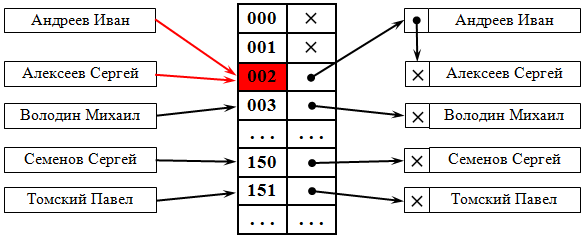

Рис. 1. Разрешение коллизий при помощи цепочек

Каждая ячейка массива является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.

Операции поиска или удаления данных требуют просмотра всех элементов соответствующей ему цепочки, чтобы найти в ней элемент с заданным ключом. Для добавления данных нужно добавить элемент в конец или начало соответствующего списка, и, в случае если коэффициент заполнения станет слишком велик, увеличить размер массива и перестроить таблицу.

При предположении, что каждый элемент может попасть в любую позицию таблицы с равной вероятностью и независимо от того, куда попал любой другой элемент, среднее время работы операции поиска элемента составляет O(1+k), где k – коэффициент заполнения таблицы.

Метод открытой адресации. В отличие от хеширования с цепочками, при открытой адресации никаких списков нет, а все записи хранятся в самой хеш-таблице. Каждая ячейка таблицы содержит либо элемент динамического множества, либо NULL.

В этом случае, если ячейка с вычисленным индексом занята, то можно просто просматривать следующие записи таблицы по порядку до тех пор, пока не будет найден ключ K или пустая позиция в таблице. Для вычисления шага можно также применить формулу, которая и определит способ изменения шага. На рис. 38.2 разрешение коллизий осуществляется методом открытой адресации. Два значения претендуют на ключ 002, для одного из них находится первое свободное (еще незанятое) место в таблице.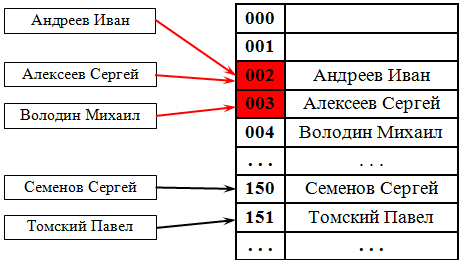

Рис. 2. Разрешение коллизий при помощи открытой адресации.

При любом методе разрешения коллизий необходимо ограничить длину поиска элемента. Если для поиска элемента необходимо более 3 – 4 сравнений, то эффективность использования такой хеш-таблицы пропадает и ее следует реструктуризировать (т.е. найти другую хеш-функцию), чтобы минимизировать количество сравнений для поиска элемента

Для успешной работы алгоритмов поиска, последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.

Алгоритмы хеширования. Существует несколько типов функций хеширования, каждая из которых имеет свои преимущества и недостатки и основана на представлении данных. Приведем обзор и анализ некоторых наиболее простых из применяемых на практике хеш-функций.

Таблица прямого доступа. Простейшей организацией таблицы, обеспечивающей идеально быстрый поиск, является таблица прямого доступа. В такой таблице ключ является адресом записи в таблице или может быть преобразован в адрес, причем таким образом, что никакие два разных ключа не преобразуются в один и тот же адрес. При создании таблицы выделяется память для хранения всей таблицы и заполняется пустыми записями. Затем записи вносятся в таблицу – каждая на свое место, определяемое ее ключом. При поиске ключ используется как адрес и по этому адресу выбирается запись. Если выбранная запись пустая, то записи с таким ключом вообще нет в таблице. Таблицы прямого доступа очень эффективны в использовании, но, к сожалению, область их применения весьма ограничена.

Назовем пространством ключей множество всех теоретически возможных значений ключей записи. Назовем пространством записей множество тех ячеек памяти, которые выделяются для хранения таблицы. Таблицы прямого доступа применимы только для таких задач, в которых размер пространства записей может быть равен размеру пространства ключей. В большинстве реальных задач размер пространства записей много меньше, чем пространства ключей. Так, если в качестве ключа используется фамилия, то, даже ограничив длину ключа десятью символами кириллицы, получаем 3310 возможных значений ключей. Даже если ресурсы вычислительной системы и позволят выделить пространство записей такого размера, то значительная часть этого пространства будет заполнена пустыми записями, так как в каждом конкретном заполнении таблицы фактическое множество ключей не будет полностью покрывать пространство ключей.

В целях экономии памяти можно назначать размер пространства записей равным размеру фактического множества записей или превосходящим его незначительно. В этом случае необходимо иметь некоторую функцию, обеспечивающую отображение точки из пространства ключей в точку в пространстве записей, то есть, преобразование ключа в адрес записи: a=h(k), где a – адрес, k – ключ.

Идеальной хеш-функцией является инъективная функция, которая для любых двух неодинаковых ключей дает неодинаковые адреса.

Метод остатков от деления. Простейшей хеш-функцией является деление по модулю числового значения ключа Key на размер пространства записи HashTableSize. Результат интерпретируется как адрес записи. Следует иметь в виду, что такая функция хорошо соответствует первому, но плохо – последним трем требованиям к хеш-функции и сама по себе может быть применена лишь в очень ограниченном диапазоне реальных задач. Однако операция деления по модулю обычно применяется как последний шаг в более сложных функциях хеширования, обеспечивая приведение результата к размеру пространства записей.

Если ключей меньше, чем элементов массива, то в качестве хеш-функции можно использовать деление по модулю, то есть остаток от деления целочисленного ключа Key на размерность массива HashTableSize, то есть:

Key % HashTableSize. Данная функция очень проста, хотя и не относится к хорошим. Вообще, можно использовать любую размерность массива, но она должна быть такой, чтобы минимизировать число коллизий. Для этого в качестве размерности лучше использовать простое число. В большинстве случаев подобный выбор вполне удовлетворителен. Для символьной строки ключом может являться остаток от деления, например, суммы кодов символов строки на HashTableSize.

На практике, метод деления – самый распространенный.

//функция создания хеш-таблицы метод деления по модулю

int Hash(int Key, int HashTableSize) {

//HashTableSize

return Key % HashTableSize;

}

Метод функции середины квадрата. Следующей хеш-функцией является функция середины квадрата. Значение ключа преобразуется в число, это число затем возводится в квадрат, из него выбираются несколько средних цифр и интерпретируются как адрес записи.

Метод свертки. Еще одной хеш-функцией можно назвать функцию свертки. Цифровое представление ключа разбивается на части, каждая из которых имеет длину, равную длине требуемого адреса. Над частями производятся определенные арифметические или поразрядные логические операции, результат которых интерпретируется как адрес. Например, для сравнительно небольших таблиц с ключами – символьными строками неплохие результаты дает функция хеширования, в которой адрес записи получается в результате сложения кодов символов, составляющих строку-ключ.

В качестве хеш-функции также применяют функцию преобразования системы счисления. Ключ, записанный как число в некоторой системе счисления P, интерпретируется как число в системе счисления Q>P. Обычно выбирают Q=P+1. Это число переводится из системы Q обратно в систему P, приводится к размеру пространства записей и интерпретируется как адрес.

Открытое хеширование. Основная идея базовой структуры при открытом (внешнем) хешировании заключается в том, что потенциальное множество (возможно, бесконечное) разбивается на конечное число классов. Для В классов, пронумерованных от 0 до В-1, строится хеш-функция h(x) такая, что для любого элемента х исходного множества функция h(x) принимает целочисленное значение из интервала 0,1,...,В-1, соответствующее классу, которому принадлежит элемент х. Часто классы называют сегментами, поэтому будем говорить, что элемент х принадлежит сегменту h(x). Массив, называемый таблицей сегментов и проиндексированный номерами сегментов 0,1,...,В-1, содержит заголовки для B списков. Элемент х, относящийся к i -му списку – это элемент исходного множества, для которого h(x)=i.

Если сегменты примерно одинаковы по размеру, то в этом случае списки всех сегментов должны быть наиболее короткими при данном числе сегментов. Если исходное множество состоит из N элементов, тогда средняя длина списков будет N/B элементов. Если можно оценить величину N и выбрать В как можно ближе к этой величине, то в каждом списке будет один или два элемента. Тогда время выполнения операторов словарей будет малой постоянной величиной, не зависящей от N.

Пример 1. Программная реализация открытого хеширования.

#include "stdafx.h"

#include

#include

using namespace std;

typedef int T; // тип элементов

typedef int hashTableIndex; // индекс в хеш-таблице

#define compEQ(a,b) (a == b)

typedef struct Node_ {

T data;// данные, хранящиеся в вершине

struct Node_ *next; // следующая вершина

} Node;

Node **hashTable;

int hashTableSize;

hashTableIndex myhash(T data);

Node *insertNode(T data);

void deleteNode(T data);

Node *findNode (T data);
int _tmain(int argc, _TCHAR* argv[]){

int i, *a, maxnum;

cout << "Введите количество элементов maxnum : ";

cin >> maxnum;

cout << "Введите размер хеш-таблицы HashTableSize : ";

cin >> hashTableSize;

a = new int[maxnum];

hashTable = new Node*[hashTableSize];

for (i = 0; i < hashTableSize; i++)

hashTable[i] = NULL;

// генерация массива

for (i = 0; i < maxnum; i++)

a[i] = rand();

// заполнение хеш-таблицы элементами массива

for (i = 0; i < maxnum; i++) {

insertNode(a[i]);

}

// поиск элементов массива по хеш-таблице

for (i = maxnum-1; i >= 0; i--) {

findNode(a[i]);

}

// вывод элементов массива в файл List.txt

ofstream out("List.txt");

for (i = 0; i < maxnum; i++){

out << a[i];

if ( i < maxnum - 1 ) out << "\t";

}

out.close();

// сохранение хеш-таблицы в файл HashTable.txt

out.open("HashTable.txt");

for (i = 0; i < hashTableSize; i++){

out << i << " : ";

Node *Temp = hashTable[i];

while ( Temp ){

out << Temp->data << " -> ";

Temp = Temp->next;

}

out << endl;

}

out.close();

// очистка хеш-таблицы

for (i = maxnum-1; i >= 0; i--) {

deleteNode(a[i]);

}

system("pause");

return 0;

}

// хеш-функция размещения вершины

hashTableIndex myhash(T data) {

return (data % hashTableSize);

}

// функция поиска местоположения и вставки вершины в таблицу

Node *insertNode(T data) {

Node *p, *p0;

hashTableIndex bucket;

// вставка вершины в начало списка

bucket = myhash(data);

if ((p = new Node) == 0) {

fprintf (stderr, "Нехватка памяти (insertNode)\n");

exit(1);

}

p0 = hashTable[bucket];

hashTable[bucket] = p;

p->next = p0;

p->data = data;

return p;

}

//функция удаления вершины из таблицы

void deleteNode(T data) {

Node *p0, *p;

hashTableIndex bucket;

p0 = 0;

bucket = myhash(data);

p = hashTable[bucket];

while (p && !compEQ(p->data, data)) {

p0 = p;

p = p->next;

}

if (!p) return;

if (p0)

p0->next = p->next;

else

hashTable[bucket] = p->next;

free (p);

}

// функция поиска вершины со значением data

Node *findNode (T data) {

Node *p;

p = hashTable[myhash(data)];

while (p && !compEQ(p->data, data))

p = p->next;

return p;

}

Листинг .

Закрытое хеширование. При закрытом (внутреннем) хешировании в хеш-таблице хранятся непосредственно сами элементы, а не заголовки списков элементов. Поэтому в каждой записи (сегменте) может храниться только один элемент. При закрытом хешировании применяется методика повторного хеширования. Если осуществляется попытка поместить элемент х в сегмент с номером h(х), который уже занят другим элементом (коллизия), то в соответствии с методикой повторного хеширования выбирается последовательность других номеров сегментов h1(х),h2(х),..., куда можно поместить элемент х. Каждое из этих местоположений последовательно проверяется, пока не будет найдено свободное. Если свободных сегментов нет, то, следовательно, таблица заполнена, и элемент х добавить нельзя.

При поиске элемента х необходимо просмотреть все местоположения h(x),h1(х),h2(х),..., пока не будет найден х или пока не встретится пустой сегмент. Чтобы объяснить, почему можно остановить поиск при достижении пустого сегмента, предположим, что в хеш-таблице не допускается удаление элементов. Пусть h3(х) – первый пустой сегмент. В такой ситуации невозможно нахождение элемента х в сегментах h4(х),h5(х) и далее, так как при вставке элемент х вставляется в первый пустой сегмент, следовательно, он находится где-то до сегмента h3(х). Но если в хеш-таблице допускается удаление элементов, то при достижении пустого сегмента, не найдя элемента х, нельзя быть уверенным в том, что его вообще нет в таблице, так как сегмент может стать пустым уже после вставки элемента х. Поэтому, чтобы увеличить эффективность данной реализации, необходимо в сегмент, который освободился после операции удаления элемента, поместить специальную константу, которую назовем, например, DEL. В качестве альтернативы специальной константе можно использовать дополнительное поле таблицы, которое показывает состояние элемента. Важно различать константы DEL и NULL – последняя находится в сегментах, которые никогда не содержали элементов. При таком подходе выполнение поиска элемента не требует просмотра всей хеш-таблицы. Кроме того, при вставке элементов сегменты, помеченные константой DEL, можно трактовать как свободные, таким образом, пространство, освобожденное после удаления элементов, можно рано или поздно использовать повторно. Но если невозможно непосредственно сразу после удаления элементов пометить освободившиеся сегменты, то следует предпочесть закрытому хешированию схему открытого хеширования.

Существует несколько методов повторного хеширования, то есть определения местоположений h(x),h1(х),h2(х),...:

линейное опробование;
квадратичное опробование;
двойное хеширование.

Линейное опробование сводится к последовательному перебору сегментов таблицы с некоторым фиксированным шагом:

адрес=h(x)+ci,

где i – номер попытки разрешить коллизию;

c – константа, определяющая шаг перебора.

При шаге, равном единице, происходит последовательный перебор всех сегментов после текущего. Квадратичное опробование отличается от линейного тем, что шаг перебора сегментов нелинейно зависит от номера попытки найти свободный сегмент:

адрес=h(x)+ci+di²,

где i – номер попытки разрешить коллизию,

c и d – константы.

Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов. Однако даже относительно небольшое число проб может быстро привести к выходу за адресное пространство небольшой таблицы вследствие квадратичной зависимости адреса от номера попытки.

Еще одна разновидность метода открытой адресации, которая называется двойным хешированием, основана на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хеш-функций:

адрес=h(x)+ih2(x).

Очевидно, что по мере заполнения хеш-таблицы будут происходить коллизии, и в результате их разрешения очередной адрес может выйти за пределы адресного пространства таблицы. Чтобы это явление происходило реже, можно пойти на увеличение длины таблицы по сравнению с диапазоном адресов, выдаваемым хеш-функцией. С одной стороны, это приведет к сокращению числа коллизий и ускорению работы с хеш-таблицей, а с другой – к нерациональному расходованию памяти. Даже при увеличении длины таблицы в два раза по сравнению с областью значений хеш-функции нет гарантии того, что в результате коллизий адрес не превысит длину таблицы. При этом в начальной части таблицы может оставаться достаточно свободных сегментов. Поэтому на практике используют циклический переход к началу таблицы.

Однако в случае многократного превышения адресного пространства и, соответственно, многократного циклического перехода к началу будет происходить просмотр одних и тех же ранее занятых сегментов, тогда как между ними могут быть еще свободные сегменты. Более корректным будет использование сдвига адреса на 1 в случае каждого циклического перехода к началу таблицы. Это повышает вероятность нахождения свободных сегментов.

В случае применения схемы закрытого хеширования скорость выполнения вставки и других операций зависит не только от равномерности распределения элементов по сегментам хеш-функцией, но и от выбранной методики повторного хеширования (опробования) для разрешения коллизий, связанных с попытками вставки элементов в уже заполненные сегменты. Например, методика линейного опробования для разрешения коллизий – не самый лучший выбор.

Как только несколько последовательных сегментов будут заполнены, образуя группу, любой новый элемент при попытке вставки в эти сегменты будет вставлен в конец этой группы, увеличивая тем самым длину группы последовательно заполненных сегментов. Другими словами, для поиска пустого сегмента в случае непрерывного расположения заполненных сегментов необходимо просмотреть больше сегментов, чем при случайном распределении заполненных сегментов. Отсюда также следует очевидный вывод, что при непрерывном расположении заполненных сегментов увеличивается время выполнения вставки нового элемента и других операций.

Пример 2. Программная реализация закрытого хеширования.

#include "stdafx.h"

#include

#include

using namespace std;

typedef int T; // тип элементов

typedef int hashTableIndex;// индекс в хеш-таблице

int hashTableSize;

T *hashTable;

bool *used;

hashTableIndex myhash(T data);

void insertData(T data);

void deleteData(T data);

bool findData (T data);

int dist (hashTableIndex a,hashTableIndex b);

int _tmain(int argc, _TCHAR* argv[]){

int i, *a, maxnum;

cout << "Введите количество элементов maxnum : ";

cin >> maxnum;

cout << "Введите размер хеш-таблицы hashTableSize : ";

cin >> hashTableSize;

a = new int[maxnum];

hashTable = new T[hashTableSize];

used = new bool[hashTableSize];

for (i = 0; i < hashTableSize; i++){

hashTable[i] = 0;

used[i] = false;

}

// генерация массива

for (i = 0; i < maxnum; i++)

a[i] = rand();

// заполнение хеш-таблицы элементами массива

for (i = 0; i < maxnum; i++)

insertData(a[i]);

// поиск элементов массива по хеш-таблице

for (i = maxnum-1; i >= 0; i--)

findData(a[i]);

// вывод элементов массива в файл List.txt

ofstream out("List.txt");

for (i = 0; i < maxnum; i++){

out << a[i];

if ( i < maxnum - 1 ) out << "\t";

}

out.close();

// сохранение хеш-таблицы в файл HashTable.txt

out.open("HashTable.txt");

for (i = 0; i < hashTableSize; i++){

out << i << " : " << used[i] << " : " << hashTable[i] << endl;

}

out.close();

// очистка хеш-таблицы

for (i = maxnum-1; i >= 0; i--) {

deleteData(a[i]);

}

system("pause");

return 0;

}

// хеш-функция размещения величины

hashTableIndex myhash(T data) {

return (data % hashTableSize);

}

// функция поиска местоположения и вставки величины в таблицу

void insertData(T data) {

hashTableIndex bucket;

bucket = myhash(data);

while ( used[bucket] && hashTable[bucket] != data)

bucket = (bucket + 1) % hashTableSize;

if ( !used[bucket] ) {

used[bucket] = true;

hashTable[bucket] = data;

}

}

// функция поиска величины, равной data

bool findData (T data) {

hashTableIndex bucket;

bucket = myhash(data);

while ( used[bucket] && hashTable[bucket] != data )

bucket = (bucket + 1) % hashTableSize;

return used[bucket] && hashTable[bucket] == data;

}

//функция удаления величины из таблицы

void deleteData(T data){

int bucket, gap;

bucket = myhash(data);

while ( used[bucket] && hashTable[bucket] != data )

bucket = (bucket + 1) % hashTableSize;

if ( used[bucket] && hashTable[bucket] == data ){

used[bucket] = false;

gap = bucket;

bucket = (bucket + 1) % hashTableSize;

while ( used[bucket] ){

if ( bucket == myhash(hashTable[bucket]) )

bucket = (bucket + 1) % hashTableSize;

else if ( dist(myhash(hashTable[bucket]),bucket) < dist(gap,bucket) )

bucket = (bucket + 1) % hashTableSize;

else {

used[gap] = true;

hashTable[gap] = hashTable[bucket];

used[bucket] = false;

gap = bucket;

bucket++;

}

}

}

}

// функция вычисления расстояние от a до b (по часовой стрелке, слева направо)

int dist (hashTableIndex a,hashTableIndex b){

return (b - a + hashTableSize) % hashTableSize;

}

Листинг. До сих пор рассматривались способы поиска в таблице по ключам, позволяющим однозначно идентифицировать запись. Такие ключи называются первичными. Возможен вариант организации таблицы, при котором отдельный ключ не позволяет однозначно идентифицировать запись. Такая ситуация часто встречается в базах данных. Идентификация записи осуществляется по некоторой совокупности ключей. Ключи, не позволяющие однозначно идентифицировать запись в таблице, называются вторичными ключами. Даже при наличии первичного ключа, для поиска записи могут быть использованы вторичные.

Идея хеширования впервые была высказана Г.П. Ланом при создании внутреннего меморандума IBM в январе 1953 г. с предложением использовать для разрешения коллизий метод цепочек. Примерно в это же время другой сотрудник IBM, Жини Амдал, высказала идею использования открытой линейной адресации. В открытой печати хеширование впервые было описано Арнольдом Думи (1956 год), указавшим, что в качестве хеш-адреса удобно использовать остаток от деления на простое число. А. Думи описывал метод цепочек для разрешения коллизий, но не говорил об открытой адресации. Подход к хешированию, отличный от метода цепочек, был предложен А.П. Ершовым (1957 год), который разработал и описал метод линейной.

ЗАКЛЮЧЕНИЕ

Процесс поиска данных в больших объемах информации сопряжен с временными затратами, которые обусловлены необходимостью просмотра и сравнения с ключом поиска значительного числа элементов. Сокращение поиска возможно осуществить путем локализации области просмотра. Например, отсортировать данные по ключу поиска, разбить на непересекающиеся блоки по некоторому групповому признаку или поставить в соответствие реальным данным некий код, который упростит процедуру поиска.

В настоящее время используется широко распространенный метод обеспечения быстрого доступа к информации, хранящейся во внешней памяти – хеширование.

В данной учебной практике мы разобрали общие характеристики хеш-функций, изучили различные сферы применения функций хеширования и разобрали некоторые примеры, Привели обзор и анализ некоторых наиболее простых из применяемых на практике алгоритмов хеш-функций.

СПИСОК ЛИТЕРАТУРЫ

Программно-аппаратная защита информации : учеб, пособие / И.А. Савельев. - М. : Финуниверситет, 2014 - 156 с.
High Quality Content by WIKIPEDIA articles! Tiger — хеш-функция / Рос Андерсон и Эл Бихам / 2012-104 с.
Handbook of Applied Cryprography / Альфред Менезес, Пол ван Ооршот, и Скотт Ванстоун / 1996-816 с.
Технические средства и методы защиты информации : учеб, пособие / А.П. Зайцев и др. - М. : Горячая линия - Телеком, 2012. - 615 с.
Информационная безопасность : учеб, пособие / Т.Л. Партыка, И.И. Попов. - М. : ФОРУМ, 2012. - 432 с.
https://intuit.ru/studies/courses/648/504/lecture/11467?page=1
https://russianblogs.com/article/7525406446/
https://revolution.allbest.ru/programming/00716985_0.html
https://ru.wikipedia.org/wiki/Хеш-функция

1 2 3 4