ЛР1_Фрактальная графика. КГ_ФГ_ЛР1_В1. Отчет по выполнения лабораторной работы по дисциплине Компьютерная графика
 Скачать 163.47 Kb. Скачать 163.47 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования ТОМСКИЙ ГОСУДАРСТВЕННЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра автоматизации обработки информации (АОИ) ФРАКТАЛЬНАЯ ГРАФИКА Отчет по выполнения лабораторной работы по дисциплине «Компьютерная графика» Вариант № 1 Выполнил: Студент ФДО гр. З-429П10-1 А. Д. Кутукова 28.02.2022 Проверил: Доцент каф. АОИ ТУСУР, канд. тех. наук Т. О. Перемитина 2022 ОглавлениеВведение 3 Используемая среда программирования 4 Метод решения задачи 5 Важные фрагменты листинга исходного кода 6 Описание функциональных возможностей разработанного приложения 6 Заключение 8 Приложение 9 Введение При выполнения данной лабораторной работы были поставлены цель и задание. Цель работы: изучение теоретических основ фрактальной графики, приобретение практических навыков построения алгебраических фракталов. Задание: реализовать программу, строящую фрактал с заданными границами расчета 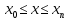 , , 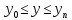 . . Согласно номеру варианту был дан вид фрактала и границы расчета. Вид фрактала: Мандельброта. Границы расчета: 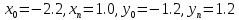 . .Используемая среда программирования В ходе выполнения лабораторной работы использовались язык программирования C++, графическая библиотека OpenGL. Реализация программы происходила в интегрированной среде разработки программного обеспечения и ряда других инструментов Microsoft Visual Studio 2019. Язык программирования С++ представляет высокоуровневый компилируемый язык программирования общего назначения со статической типизацией, который подходит для создания самых различных приложений. На сегодняшний день С++ является одним из самых популярных и распространенных языков. OpenGL (Open Graphic Library) – библиотека графических функций, интерфейс для графических прикладных программ. Разработана Silicon Graphics. OpenGL является на данный момент одним из самых популярных программных интерфейсов (API) для разработки приложений в области двумерной и трехмерной графики. Библиотека насчитывает около 120 различных команд, которые программист использует для задания объектов и операций, необходимых для написания интерактивных графических приложений. Microsoft Visual Studio - полнофункциональная интегрированная среда разработки (IDE) с поддержкой популярных языков программирования, среди которых С, C++, VB.NET, C#, F#, JavaScript, Python. Функциональность Visual Studio охватывает все этапы разработки программного обеспечения, предоставляя современные инструменты для написания кода, проектирования графических интерфейсов, сборки, отладки и тестирования приложений. Возможности Visual Studio могут быть дополнены путем подключения необходимых расширений. Метод решения задачи Фракталом Мандельброта названа фигура, которая порождается очень простым циклом. Для создания этого фрактала необходимо для каждой точки изображения выполнить цикл итераций согласно формуле: 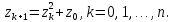 Величины 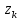 – это комплексные числа, – это комплексные числа, 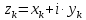 , причем стартовые значения , причем стартовые значения 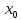 и и 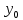 – это координаты точки изображения. Для каждой точки изображения итерации выполняются ограниченное количество раз (n) или до тех пор, пока модуль числа – это координаты точки изображения. Для каждой точки изображения итерации выполняются ограниченное количество раз (n) или до тех пор, пока модуль числа 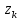 не превышает 2. Модуль комплексного числа равен корню квадратному из не превышает 2. Модуль комплексного числа равен корню квадратному из 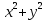 . Для вычисления квадрата величины . Для вычисления квадрата величины 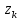 можно воспользоваться формулой: можно воспользоваться формулой: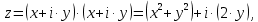 поскольку 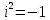 . .Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне x = (от − 2.2 до 1), y = (от − 1.2 до 1.2). Для того чтобы получить изображение в растре, необходимо пересчитывать координаты этого диапазона в пиксельные. Важные фрагменты листинга исходного кода Ниже приведены важные фрагменты листинга исходного кода программы с комментариями. //Функция, отвечающая за отображения окна, в котором происходит построение фрактала Мандельброта int main(int argc, char** argv) { glutInit(&argc, argv); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); glutInitWindowSize(600, 600); glutInitWindowPosition(350, 20); glutCreateWindow("Фрактальная графика Вариант 1"); myInit(); glutDisplayFunc(myDisplay); glutMainLoop(); } //Функция, отвечающая за работу с координатами точек на комплексной плоскости void myInit() { glClearColor(1.0, 1.0, 1.0, 0.0); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluOrtho2D(-2.2, 1, -1.2, 1.2); } //Функция, отвечающая за цикл итераций для фрактала Мандельброта void myDisplay() { glClear(GL_COLOR_BUFFER_BIT); glColor3f(1.0, 1.0, 1.0); DrawMandelbrot(600); glFlush(); } //Функция, отвечающая за построение фрактала Мандельброта void DrawMandelbrot(int iterations) { double xTemp, yTemp; double x, y; glPointSize(1.0); glColor3f(0, 0, 0); glBegin(GL_POINTS); for (double a = -2.2; a < 1; a += 0.001) { for (double b = -1.2; b < 1.2; b += 0.001) { x = a, //x и y изначально - координаты исследуемой точки y = b; int iterator = 0; //счетчик while (iterator < iterations && x * x + y * y < 4) { xTemp = x * x - y * y + a; yTemp = 2 * x * y + b; x = xTemp; y = yTemp; iterator++; } if (iterator == iterations) glVertex2d(a, b); } } glEnd(); } Описание функциональных возможностей разработанного приложения Главная функция разработанного консольного приложения заключается в вызове окна, в котором реализуется построение фрактала Мандельброта согласно заданным границам расчета 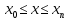 , , 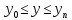 . . Согласно номеру варианта были даны следующие границы расчета: 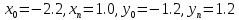 . .Заключение По результатам выполненной работы можно сделать следующие выводы: Были изучены теоретические основы фрактальной графики; Были приобретены практические навыки построения алгебраических фракталов; Была реализована программа, строящая фрактал Мандельброта с заданными границами расчета: 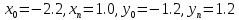 . .Исходя из выше сказанного, можно сделать заключение о том, что цели и задачи данной лабораторной работы были выполнены. Приложение 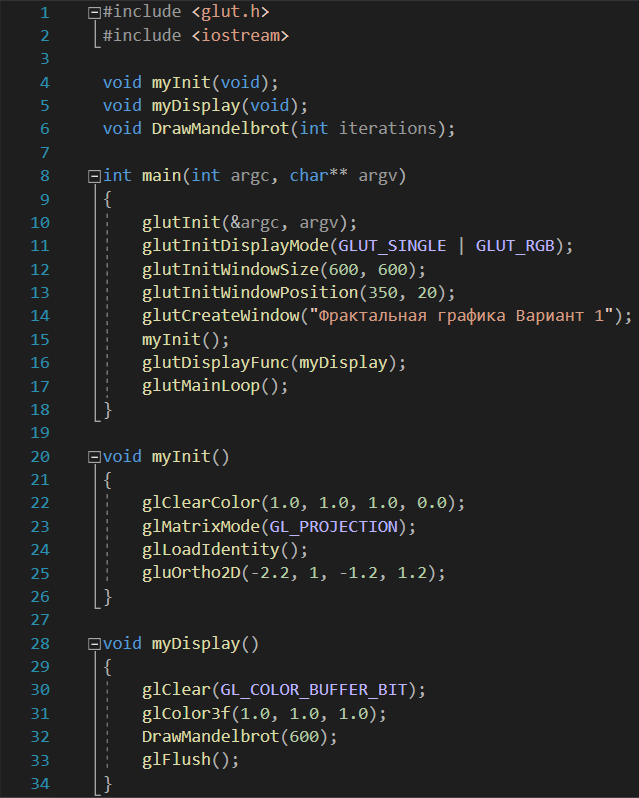 Рис. 1 – Программный код приложения 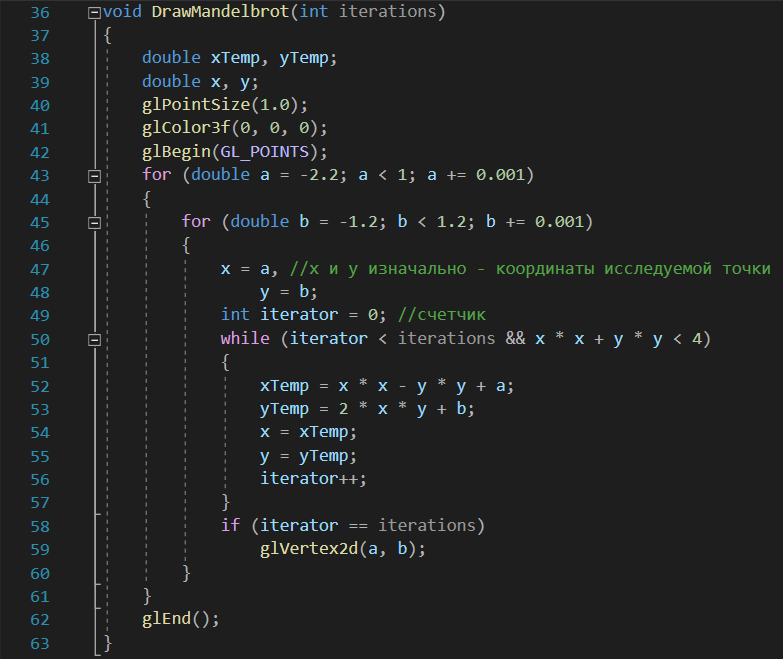 Рис. 1.2 – Программный код приложения Рис. 1.2 – Программный код приложения Рис. 2 – Результат тестирования реализуемого приложения Рис. 2 – Результат тестирования реализуемого приложения |
