2 отчёт. Отчет по выполнению практического задания 2
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Отчет по выполнению практического задания 2 Тема. Эмпирический анализ алгоритмов сортировки Дисциплина Структуры и алгоритмы обработки данных Выполнил
Москва 2021 1ЗаданияЗадание 1. 1)Составить программу сортировки одномерного целочисленного массива A[n], используя алгоритм прямого выбора. Провести тестирование программы на исходном массиве, сформированном вводом с клавиатуры. Рабочий массив A сформировать с использованием генератора псевдослучайных чисел. Провести контрольные прогоны программы для размеров массива n = 100, 1000, 10000, 100000 и 1000000 элементов с вычислением времени выполнения T(n). Полученные результаты свести в сводную таблицу. Построить график зависимости времени выполнения программы от размера массива. Примечание. Массив может быть статическим или динамическим по вашему усмотрению. 2)Провести эмпирическую (практическую) оценку вычислительной сложности алгоритма, для чего предусмотреть в программе подсчет фактического количества операций сравнения Сф и количества операций перемещения Мф. Полученные результаты свести в сводную таблицу. Таблица 1 Сводная таблица результатов
3)Построить в одной координатной плоскости графики зависимости теоретической О(n)=f(С+М) и эмпирической (Сф+Мф) вычислительной сложности алгоритма от размера массива n. 4)Провести анализ полученных результатов. Сделать выводы о проделанной работе, основанные на полученных результатах. Задание 2 1) Провести дополнительные прогоны программы на рабочих массивах, отсортированных строго в убывающем и возрастающем порядке значений элементов. Провести анализ зависимости (или независимости) алгоритма сортировки от исходной упорядоченности массива. 2) Провести программную реализацию алгоритмов «Простой вставки», «Простого обмена» с последующим сравнительным анализом полученных результатов контрольных прогонов и построением соответствующих графиков. Отчет по заданию 1Была составлена программа сортировки одномерного целочисленного массива, с использованием алгоритма прямого выбора. Ниже представлен код функции, реализующей данный алгоритм: void LinearSelection(int* arr, int size) { long long int Cf = 0; long long int Mf = 0; unsigned int start = clock(); for (int i = 0; i < size - 1; i++) { int min = i; for (int j = i + 1; j < size; j++) { Cf++; if (arr[j] < arr[min]) { min = j; } } if (min != i) { Mf++; std::swap(arr[i], arr[min]); } } unsigned int end = clock(); std::cout << "Cf = " << Cf; std::cout << "; Mf = " << Mf; std::cout << "; Time = " << (end - start) / (CLOCKS_PER_SEC) << '\n'; } Была проведена эмпирическая оценка вычисленной сложности алгоритма. Было подсчитано фактическое количество операций сравнения Сф и фактическое количество операций перемещения Мф. Результаты были занесены в таблицу 1. Таблица 1 Сводная таблица результатов
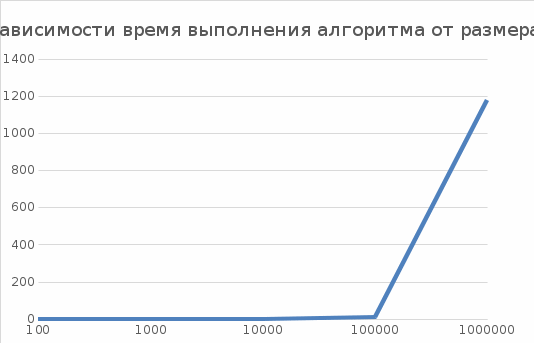 На одной координатной плоскости были построены графики зависимости теоретической и эмпирической вычисленной сложности алгоритма от размера массива. 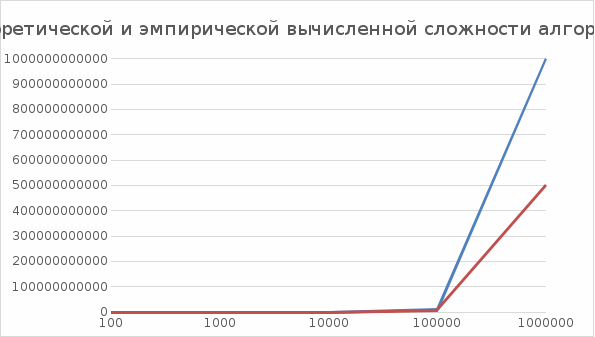 Вывод По результатам выполненной работы видно, что сложность данного алгоритма очень быстро растет при увеличении размера массива. Также можно заметить, что фактическая сложность алгоритма заметно меньше, чем теоретическая, однако, она все равно является очень большой при больших размерах массива. Отчет по заданию 2Были проведены дополнительные прогоны программы на отсортированных массивах. Результаты представлены в таблицах 2 и 3. Таблица 2 Результаты для отсортированного по возрастанию массива
Таблица 3 Результаты для отсортированного по убыванию массива
Исходя из полученных результатов видно, что для отсортированных массивов заметно уменьшается количество перемещений. Причем, для отсортированного по возрастанию массива количество перемещений уменьшается почти в 2 раза, а для отсортированных по убыванию вообще рано 0. При больших размерах массива это является весомым уменьшением количества операций, но оно не сильно уменьшает время работы программы. Были реализованы алгоритмы «Простой вставки» и «Простого обмена». Ниже представлен код функций, которые реализуют данные алгоритмы. Простая вставка: bool InsertionsComp(int j, int num, int arr_elem, long long int *Cf) { *Cf += 1; if ((j >= 0) && (arr_elem > num)) { return true; } return false; } void Insertions(int* arr, int size) { long long int Cf = 0; long long int Mf = 0; unsigned int start = clock(); for (int i = 1; i < size; i++) { int j = i - 1; int num = arr[i]; while (InsertionsComp(j, num, arr[j], &Cf)) { std::swap(arr[j], arr[j + 1]); Mf++; j--; } arr[j + 1] = num; Mf++; } unsigned int end = clock(); std::cout << "Cf = " << Cf; std::cout << "; Mf = " << Mf; std::cout << "; Time = " << (end - start) / CLOCKS_PER_SEC << '\n'; } Простой обмен: void Trade(int* arr, int size) { long long int Cf = 0; long long int Mf = 0; unsigned int start = clock(); for (int i = size - 1; i > 0; i--) { for (int j = 0; j < i; j++) { Cf++; if (arr[j] > arr[j + 1]) { Mf++; std::swap(arr[j], arr[j + 1]); } } } unsigned int end = clock(); std::cout << "Cf = " << Cf; std::cout << "; Mf = " << Mf; std::cout << "; Time = " << (end - start) / CLOCKS_PER_SEC << '\n'; } Для алгоритма простой вставки: Таблица 4 Сводная таблица результатов
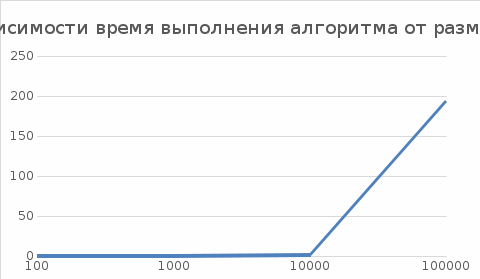 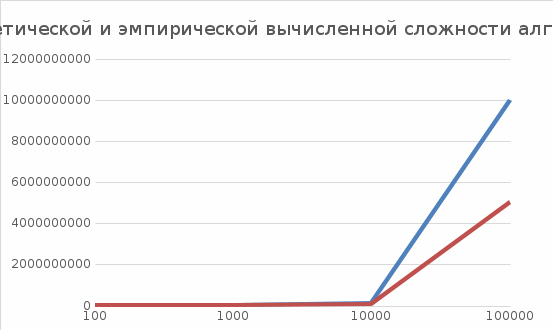 Для алгоритма простого обмена: Таблица 5 Сводная таблица результатов
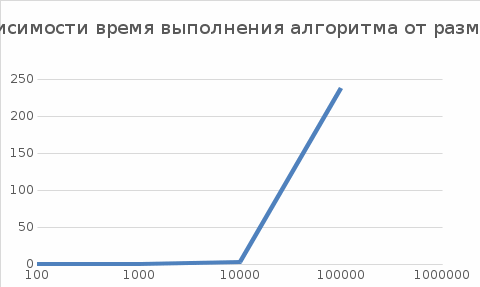 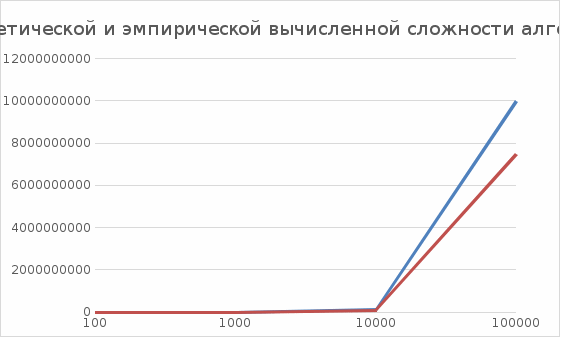 В ходе выполнения проверок для алгоритмов «Простой вставки» и «Простого обмена», был сделан вывод, что алгоритм «Простой вставки» эффективнее по количеству операций, чем алгоритм «Простого обмена». Это можно видеть в сводных таблицах и на графиках зависимости теоретической и эмпирической вычисленной сложности алгоритма от размера массива. Для небольших массивов данные алгоритмы работают достаточно быстро, но уже начиная со 100000 алгоритм «Простой вставки» начинает работать быстрее. |


