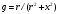Практика радиопередающие и радиоприемные устройства. 1 практика 12 вариант. Отчет по выполнению практической работе 1 по курсу Радиопередающие и радиоприёмные устройства
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Юго-Западный государственный университет» (ЮЗГУ) Кафедра информационных систем и технологий Отчет по выполнению практической работе № 1 по курсу: «Радиопередающие и радиоприёмные устройства» на тему «Задания общей практики № 1-8» Выполнил: студент группы ИТ-71з Комаренко С.В. Проверил: ст. преподаватель Коптев Д.С. Задание 1. Записать алгебраическую, тригонометрическую и показательную формы записи комплексного и комплексно сопряженного числа. Комплексное число имеет следующий вид: 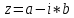 Комплексно-сопряженное число имеет вид 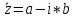 Тригонометрическая форма записи имеет следующий вид: 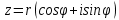 и, соответственно, и, соответственно, 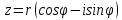 Показательная форма: 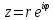 и и 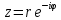 Задание 2. Что такое комплексная амплитуда и как она записывается математически? Комплексная амплитуда, представление амплитуды А и фазы гармонического колебания 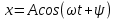 с помощью комплексного числа с помощью комплексного числа 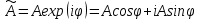 . .Задание 3. Представить на графиках: а) алгебраическую форму комплексного и комплексно сопряженного числа; б) комплексную амплитуду; в) показательную форму комплексного и комплексно сопряженного числа; г) тригонометрическую форму комплексного и комплексно сопряженного числа; 1) Алгебраическая форма: 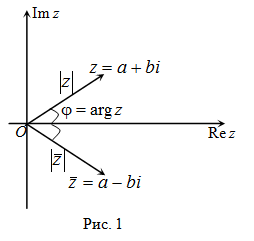 2) Комплексная амплитуда:  3) Тригонометрическая и показательные формы связаны формулой Эйлера и имеют вид: 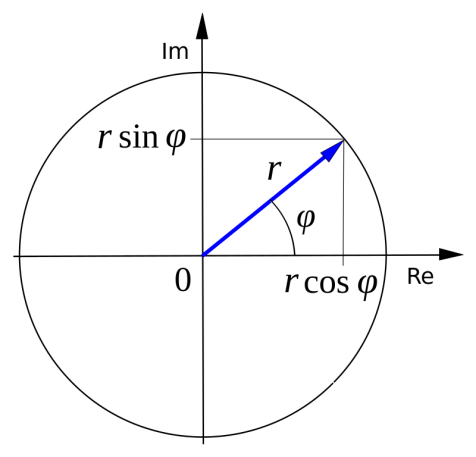 Задание 4. . Изобразить на графике в осях напряжение – время две косинусоидальные кривые 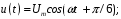 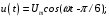 Объяснить словами, какая из кривых опережает по фазе, а какая отстает. 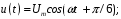 Данная кривая отстает по фазе  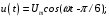 Данная кривая опережает по фазе 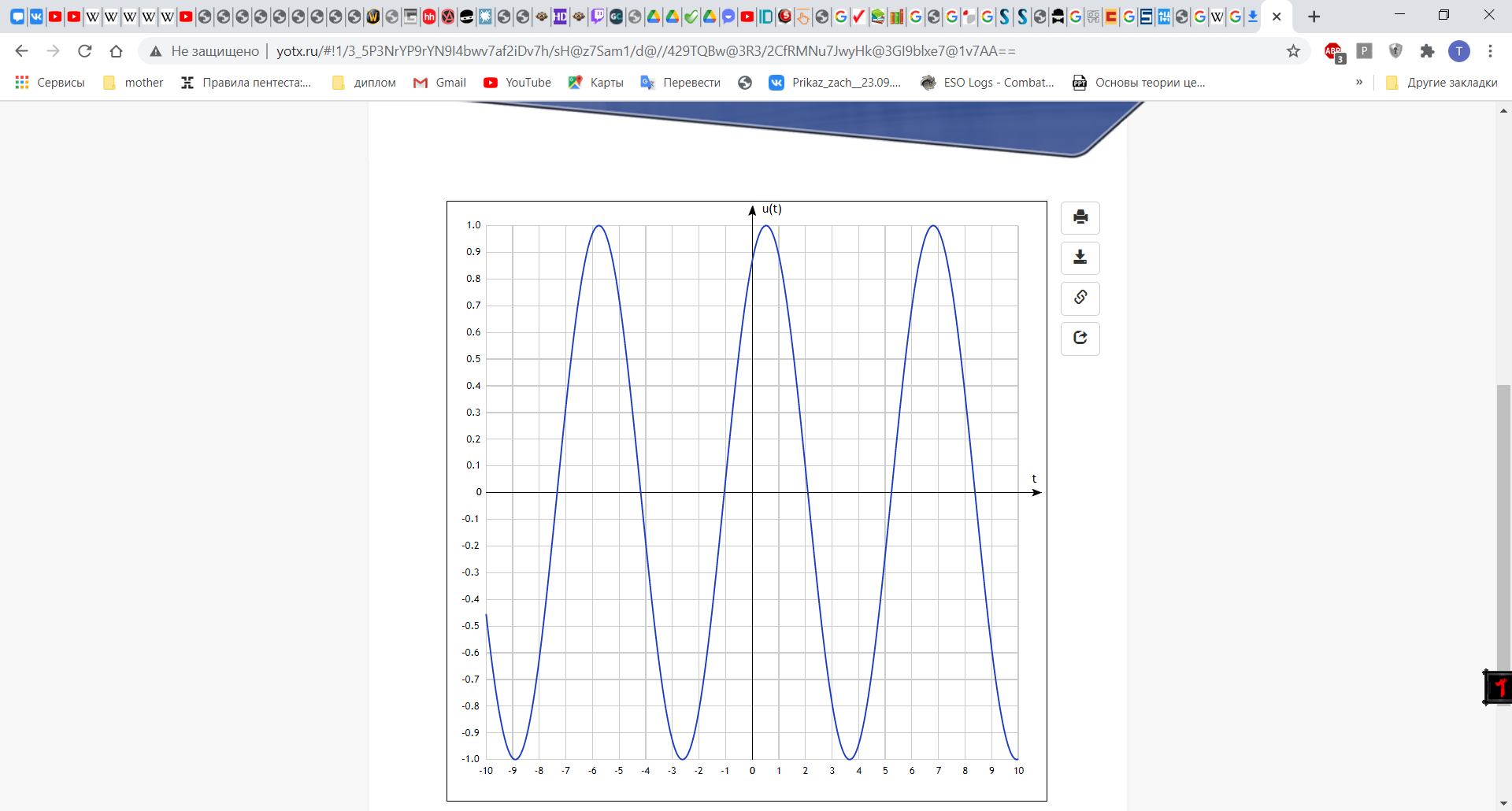 Задание 5. Изобразить график функции 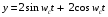  Задание 6. Комплексное сопротивление 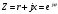 Найти модуль сопротивления 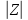 и аргумент φ, активную и реактивную проводимости до третьей значащей цифры после запятой при исходных данных активного и реактивного сопротивлений, представленных в таблице 6. и аргумент φ, активную и реактивную проводимости до третьей значащей цифры после запятой при исходных данных активного и реактивного сопротивлений, представленных в таблице 6.Решение: 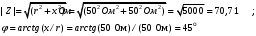 Комплексная проводимость 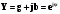 откуда активная проводимость 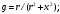 реактивная проводимость 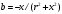
Задание 7 Изобразить комплексное сопротивление и проводимость на комплексной плоскости с рассчитанными их значениями модуля и фазы. Комплексное сопротивление: 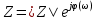 Комплексная проводимость: Y = 1/Z 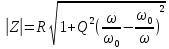 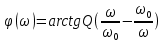 Задание 8. Найти полные комплексные входные сопротивление и проводимость последовательного колебательного контура на частотах, указанных в таблице 8 (сопротивление: реактивное - x; модуль 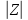 ; аргумент – φ; проводимость: активная – g; реактивная – b; модуль ; аргумент – φ; проводимость: активная – g; реактивная – b; модуль 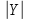 ; аргумент - ψ) при следующих исходных данных ; аргумент - ψ) при следующих исходных данныхr=0,5Ом; L=1мкГн; С=100пФ. Расчеты провести с точностью до четвертой значащей цифры после запятой. Полное сопротивление последовательного колебательного контура равно 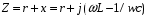 В случае настройки колебательного контура в резонанс его реактивное сопротивление 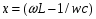 равно нулю. Остается только активное сопротивление r. равно нулю. Остается только активное сопротивление r.При этом можно рассчитать частоту настройки контура из условия равенства реактивностей 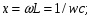 тогда при L=1мкГн и С=100пФ 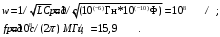 В случае расстройки колебательного контура его реактивное сопротивление 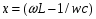 отлично от нуля и может быть рассчитано по исходным данным ω, L и С. отлично от нуля и может быть рассчитано по исходным данным ω, L и С.Модуль сопротивления 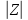 ; аргумент сопротивления – φ; проводимость: активная – g; реактивная – b; модуль проводимости ; аргумент сопротивления – φ; проводимость: активная – g; реактивная – b; модуль проводимости 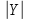 ; аргумент проводимости – ψ рассчитываются по формулам: ; аргумент проводимости – ψ рассчитываются по формулам: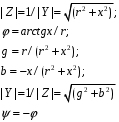
| |||||||||||||||||||||||||||||||||||||||||||||||||

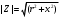 [Ом]
[Ом]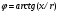 [град]
[град]