2.Тестирование методом белого ящика. Отчет по выполненной лабораторной работе. Итоговая оценка складывается из оценок по трем указанным составляющим

• Название: Отчет по выполненной лабораторной работе. Итоговая оценка складывается из оценок по трем указанным составляющим
• Дата: 18.11.2022
• Размер: 126.37 Kb.
• Имя файла: 2.Тестирование методом белого ящика.docx
• Тип: Отчет; #795346

Министерство науки и высшего образования Российской Федерации

Казанский национальный исследовательский технический университет – КАИ им. А.Н. Туполева

Институт компьютерных технологий и защиты информации

Отделение СПО ИКТЗИ «Колледж информационных технологий»

ПОДДЕРЖКА И ТЕСТИРОВАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ

Методические указания к лабораторным работам

Казань 2021

Составитель преподаватель СПО ИКТЗИ Пелагеин Александр Александрович

Методические указания к лабораторным работам по дисциплине «ПОДДЕРЖКА И ТЕСТИРОВАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ» предназначены для студентов направления подготовки 09.02.07 «Информационные системы и программирование»

КНИТУ-КАИ, 2022

ОГЛАВЛЕНИ

ПОДДЕРЖКА И ТЕСТИРОВАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ 1

Теоретическая часть 5

ПОДДЕРЖКА И ТЕСТИРОВАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ 1

ПРОЦЕСС СДАЧИ ВЫПОЛНЕННОЙ РАБОТЫ

По итогам выполнения работы студент:

1. 
   демонстрирует преподавателю выполненную работу;
   
2. 
   демонстрирует приобретённые знания и навыки отвечает на пару небольших вопросов преподавателя по выполненной работе,
   

возможностям её доработки;

3. 
   демонстрирует отчет по выполненной лабораторной работе.
   

Итоговая оценка складывается из оценок по трем указанным составляющим.

Шаблон оформления отчета представлен в приложении 1. Требования к формированию отчета представлены в приложении 2.

ЛАБОРАТОРНАЯ РАБОТА №2.

«Тестирование программ методом «белого ящика»

Цель работы. Отработать навыки составления и тестирования программ как «белого ящика».

Теоретическая часть

Тестирование – это процесс многократного выполнения программы с целью обнаружения максимального количества ошибок. Программа тестируется для того, чтобы повысить уровень надежности программы. Тестирование является составной частью отладки и включает в себя два вида деятельности: разработка тестов и непосредственное тестирование по ним.

Особенность тестировании программ как «белый ящик» заключается в следующем:

• 
  Известна: внутренняя структура программы.
  
• 
  Исследуются: внутренние элементы программы и связи между ними (рис. 5.1).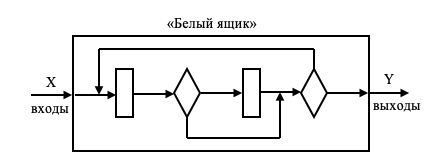
  

Рисунок 5.1 – Тестирование «белого ящика»

Объектом тестирования здесь является не внешнее, а внутреннее поведение программы. Проверяется корректность построения всех элементов программы и правильность их взаимодействия друг с другом.

Методы белого ящика

1. Метод покрытия операторов

Критерием этого метода является выполнение каждого оператора хотя бы один раз. Этот критерий является достаточно слабым, так как выполнение каждого оператора хотя бы один раз условие необходимое, но недостаточное для результирующего условия.

2. Метод покрытия решений

Согласно этому методу должно быть написано достаточное количество тестов, такое, что каждое решение на этих тестах выполняется по крайней мере один раз и при этом каждый оператор должен выполняться хотя бы один раз.

3. Метод покрытия условий

В этом случае записывают число тестов достаточное для того, чтобы всевозможные результаты каждого условия в решении выполнялись по крайней мере один раз.

4. Метод покрытия решений/условий

Этот метод требует достаточного набора тестов, чтобы возможные результаты каждого условия в решении выполнялись по крайней мере один раз и каждой точке входа передавалось управление по крайней мере один раз.

Тестирование программы с использованием потокового графа.

Для представления программы используется потоковый граф (рис. 5.2). Особенности потокового графа:

1. Граф строится отображением управляющей структуры программы. В ходе отображения закрывающие скобки условных операторов и операторов циклов (end if; end loop) рассматриваются как отдельные (фиктивные) операторы.

2. Узлы (вершины) потокового графа соответствуют линейным участкам программы, включают один или несколько операторов программы.

3. Дуги потокового графа отображают поток управления в программе (передачи управления между операторами). Дуга – это ориентированное ребро.

4. Различают операторные и предикатные узлы. Из операторного узла выходит одна дуга, а из предикатного – две дуги.

5. Предикатные узлы соответствуют простым условиям в программе. Составное условие программы отображается в несколько предикатных узлов. Составным называют условие, в котором используется одна или несколько булевых операций (OR, AND).

Цикломатическая сложность

Цикломатическая сложность – метрика ПО, которая обеспечивает количествен­ную оценку логической сложности программы. В способе тестирования базового пути цикломатическая сложность определяет:

• 
  количество независимых путей в базовом множестве программы;
  
• 
  верхнюю оценку количества тестов, которое гарантирует однократное выполнение всех операторов.
  

Независимым называется любой путь, который вводит новый оператор обработки или новое условие. В терминах потокового графа независимый путь должен содержать дугу, не входящую в ранее определенные пути.

Путь начинается в начальном узле, а заканчивается в конечном узле графа. Независимые пути формируются в порядке от самого короткого к самому длинному. Каждый новый путь включает новую дугу.

Все независимые пути графа образуют базовое множество.

Свойства базового множества:

1) тесты, обеспечивающие его проверку, гарантируют:

- однократное выполнение каждого оператора;

- выполнение каждого условия по True-ветви и по False-ветви;

2) мощность базового множества равна цикломатической сложности потокового графа.

Мощность базового множества дает априорную оценку коли­чества независимых путей, которое имеет смысл искать в графе.

Цикломатическая сложность вычисляется одним из трех способов:

цикломатическая сложность равна количеству регионов потокового графа;

цикломатическая сложность определяется по формуле: V(G)=E-N+2, где Е – количество дуг, N – количество узлов потокового графа;

цикломатическая сложность формируется по выражению V(G) = р + 1, где р – количество предикатных узлов в потоковом графе G.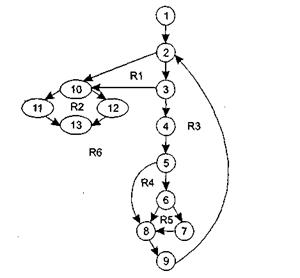



Рисунок 5.2 – Пример потокового графа

Задание на лабораторную работу

Выполнение работы предусматривает следующую последовательность действий:

1. Построение потокового графа программы;

2. Построение базового множества независимых линейных путей;

3. Составление тестовых вариантов;

4. Выполнение тестирования;

5. Оформление результатов тестирования.

Если в программе нет ошибок, то искусственно по согласованию с преподавателем вводятся ошибки для проверки эффективности тестирования

В отчет по лабораторной работе включаются:

1. Текст программы;

2. Потоковый граф;

3. Множество независимых линейных путей;

4. Тестовые варианты;

5. Результаты тестирования.

Варианты задания

1. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N, A_N+1 вещественных чисел. Определить наибольшее из нечетных и количество четных чисел, входящих в этот массив.

2. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N целых чисел. Получить массив, который отличается от исходного тем, что все нечетные элементы удвоены, а четные получены сложением собственного значения с первоначальным значением последующего нечетного.

3. Даны натуральное число N (N>5) и одномерный массив A₁, A₂, …, A_N символьных элементов. Определить три максимальных и два минимальных значения этого массива.

4. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N целых чисел. Определить наименьшее положительное среди A₁, A₂, …, A_N.

5. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N вещественных чисел. В данном массиве определить число соседств двух положительных чисел.

6. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N целых чисел. В данном массиве определить число соседств двух чисел разного знака.

7. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N символьных элементов. Определить, является ли данный массив упорядоченным по убыванию.

8. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N натуральных чисел. Для каждого элемента определить число его вхождений в данный массив.

9. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N вещественных чисел. Получить все элементы, входящие в данный массив по одному разу.

10. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N символьных элементов. Получить все элементы, входящие в данный массив более одного раза.

11. Даны натуральное число N и два одномерных массива A₁, A₂, …, A_N и B₁, B₂, …, B_N целых чисел. Определить верно ли, что эти массивы отличаются только порядком следования элементов.

12. Дан одномерный массив A₁, A₂, …, A₁₀ вещественных чисел. Получить наибольшее среди А₁+А₁₀, А₂+А₉, …, А₅+А₆.

13. Дан одномерный массив A₁, A₂, …, A₁₀ целых чисел. Получить наименьшее среди А₁+А₆, А₂+А₇, …, А₅+А₁₀.

14. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N целых чисел. Определить наибольшее и наименьшее значения, полученные значения рассматривать как концы отрезка. Разбить отрезок на 5 диапазонов значений по возрастанию и подсчитать частоту попаданий элементов массива в каждый из этих диапазонов.

15. Даны натуральное число N (N – четное) и одномерный массив A₁, A₂, …, A_N логических элементов. Выполнить циклический сдвиг первой половины массива справа налево, а второй – слева направо.

16. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N символьных элементов. Выполнить линейный сдвиг слева направо элементов, расположенных в нечетных позициях, на 3 позиции. Элементы четных позиций оставить на прежнем месте.

17. Даны натуральное число N (N – четное) и одномерный массив A₁, A₂, …, A_N вещественных чисел. Заменить элементы, расположенные в четных позициях первой половины массива, удвоенными значениями элементов, расположенных в нечетных позициях второй половины массива.

18. Даны натуральное число N и одномерный массив A₁, A₂, …, A_N целых чисел. Найти наименьший элемент в наиболее длинной непрерывной последовательности положительных значений.

Пример практической части

1. 
   Написать программу согласно варианту, на языке программирования C#. Условие: Даны натуральное число N и одномерный массив А1, А2, ..., AN целых чисел. В данном массиве определить число соседств двух чисел разного знака
   
2. 
   На рисунке 1 показан алгоритм программы, а на рисунке 2 изображен потоковый граф программы.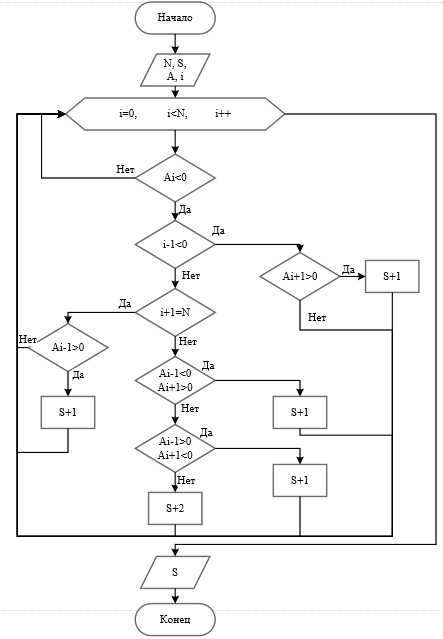
   

Рисунок 1 – Алгоритм программы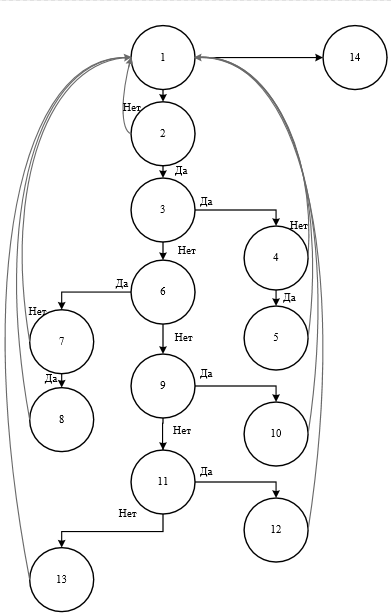



Рисунок 2 – Потоковый граф программы

3. 
   Определить цикломатическую сложность потокового графа.
   

V(G)= 20(E) – 14(N) + 2 = 8 или по второй формуле

V(G)= 7(P) + 2 = 8

4. 
   Построить базовое множество независимых линейных путей.
   

1-2-1-14, 1-2-3-4-1-14 и 1-2-3-4-5-1-14, 1-2-3-6-7-1-14 и 1-2-3-6-7-8-1-14,1-2-3-6-9-10-1-14, 1-2-3-6-9-11-12-1-14 и 1-2-3-6-9-11-13-1-14.

5. 
   Составить тестовые варианты.
   

Тестовые варианты идентичны базовым путям.

6. 
   Выполнение тестирования (таблица 1).
   

Таблица 1 – Результат выполнения тестирования

№	Данные	Ожидаемый результат	Фактический результат	Результаты тестирования
1	А=3 В=-2 С=4	X=2 смежных элемента (1-2-3-6-9-11-13-1-14)	X=2 смежных элемента	Успешно
2	А=-1 В=-2 С=-3	X=0 смежных элементов	X=2смежных элементов	Провалено
3	А=5 В=-3 С=-7	X=1 смежный элемент (1-2-3-6-9-11-12-1-14)	X=1 смежный элемент	Успешно
4	A=3 В=3 С=3	X=0 смежных элементов (1-2-1-14)	X=0 смежных элементов	Успешно

Вопросы к лабораторной работе.

1. 
   Дайте определение цикломатической сложности и укажите способы вычисления.
   

Цикломатическая сложность – это матрица ПО, которая обеспечивает количественную оценку логической сложности программы.

Цикломатическая сложность вычисляется одним из трех способов:

1) равна количеству регионов потокового графа;

2) определяется по формуле V(G) = Е – N + 2, где Е – количество дуг, N – количество узлов потокового графа;

3) определяется по формуле V(G) = р + 1, где р – количество предикатных узлов в потоковом графе.

Вывод: изучены принципы тестирования методом «белого ящика», используя анализ граничных значений.