Главная страница
Навигация по странице:

  • "МИРЭА - Российский технологический университет"

  • ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ № 8

    		•

    Практическая работа № 8. Отчет попрактическойработе8


    Скачать 0.6 Mb.
    НазваниеОтчет попрактическойработе8
    АнкорПрактическая работа № 8
    Дата26.12.2021
    Размер0.6 Mb.
    Формат файлаdocx
    Имя файлаПрактическая работа № 8.docx
    ТипОтчет
    #318693



    МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования

    "МИРЭА - Российский технологический университет"

    РТУ МИРЭА




    Институт искусственного интеллекта

    Кафедра общей информатики (ОИ)


    ОТЧЕТ

    ПОПРАКТИЧЕСКОЙРАБОТЕ№ 8

    реализация заданной логической функции от четырех переменных на мультиплексорах 16-1, 8-1, 4-1, 2-1

    по дисциплине


    «ИНФОРМАТИКА»


    Выполнил студент группы ИКБО-35-21 Махин.Г.С.
    Принял Ассистент ОИ Тябут .Е.А.


    Практическая

    «__»_______2021 г.
    _______________

    работа выполнена






    «Зачтено»

    «__»_______2021 г.
    _______________



    Москва 2021

    СОДЕРЖАНИЕ




    РТУ МИРЭА 1

    реализация заданной логической функции от четырех переменных на мультиплексорах 16-1, 8-1, 4-1, 2-1 1

    по дисциплине 1

    СОДЕРЖАНИЕ 2

    1. ПОСТАНОВКА ЗАДАЧИ 3

    2. ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4

    2.1 ВОССТАНОВЛЕНИЕ ТАБЛИЦЫ ИСТИНОСТИ 4

    2.2 СХЕМЫ , РЕАЛИЗУЮЩИЕ ЛОГИЧЕСКУЮ ФУНКЦИЮ НА ДЕШИФРАТОРАХ ТРЕБУЕМЫМИ СПОСОБАМИ 4

    3. ВЫВОДЫ 12

    4. ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 14






    1. ПОСТАНОВКА ЗАДАЧИ


    Логическая функция от четырех переменных задана в 16-теричной векторной форме. Восстановить таблицу истинности. По таблице истинности реализовать в лабораторном комплексе логическую функцию на дешифраторах тремя

    способами:

    – используя дешифратор 4-16 и одну дополнительную схему «или»;

    – используя два дешифратора 3-8 и необходимую дополнительную логику;

    – используя пять дешифраторов 2-4 и одну дополнительную схему «или».

    Протестировать работу схем и убедиться в правильности их работы. Подготовить отчет о проделанной работе и защитить ее.





    2. ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ

    2.1 ВОССТАНОВЛЕНИЕ ТАБЛИЦЫ ИСТИНОСТИ


    Функция, заданная в 16-теричной форме имеет следующий вид: 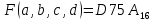.Преобразуем ее в двоичную запись: 1101011101011010 – получили столбец значений логической функции, который необходим для восстановления полной таблицы истинности (см. табл.1)

    Таблица 1 - Таблица истинности для функции F

    a
    b
    c
    d
    F

    1
    1
    1
    1
    1

    1
    1
    1
    0
    1

    1
    1
    0
    1
    0

    1
    1
    0
    0
    1

    1
    0
    1
    1
    0

    1
    0
    1
    0
    1

    1
    0
    0
    1
    1

    1
    0
    0
    0
    1

    0
    1
    1
    1
    0

    0
    1
    1
    0
    1

    0
    1
    0
    1
    0

    0
    1
    0
    0
    1

    0
    0
    1
    1
    1

    0
    0
    1
    0
    0

    0
    0
    0
    1
    1

    0
    0
    0
    0
    0

    2.2 СХЕМЫ , РЕАЛИЗУЮЩИЕ ЛОГИЧЕСКУЮ ФУНКЦИЮ НА ДЕШИФРАТОРАХ ТРЕБУЕМЫМИ СПОСОБАМИ


    Для реализации заданной функции на мультиплексоре 16-1 выполним следующее. Разместим мультиплексор на рабочей области лабораторного комплекса и сделаем ему следующие настройки:

    – свойство «выбирающие биты» сделаем равным 4;

    – «разрешающий вход» — нет;

    – «положение выбирающего входа» — сверху (сделано в данном примере

    для удобства, можно оставить значение по умолчанию).

    Количество информационных входов мультиплексора соответствует количеству значений логической функции. Поэтому просто подадим значения функции на соответствующие входы. Для этого удобно воспользоваться логическими константами из раздела «Провода» библиотеки элементов Logisim. На адресные (выбирающие) входы мультиплексора подадим при помощи шины значения логических переменных. Несмотря на использование шины, следует помнить, что младшая переменная подается на младший адресный вход, а старшая – на старший. Собранная и протестированная схема показана на рисунок. 1. Тестирование подтвердило правильность работы схемы.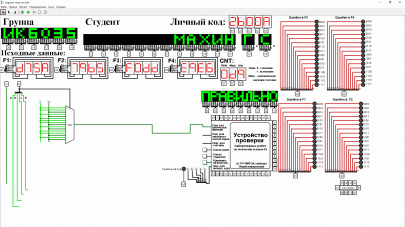



    Рисунок. 1 Тестирование схемы, реализующей логическую функцию

    на мультиплексоре 16-1

    Выполним реализацию заданной логической функции при помощи мультиплексора 8-1.Мультиплексор 8-1 имеет 3 адресных входа, что не позволяет подать на эти входы все 4 логические переменные, как это было сделано в предыдущем случае. Однако мы можем в качестве адресных переменных выбрать любые три из имеющихся, а оставшуюся четвертую рассматривать наравне с логическими константами как элемент исходных данных для информационных входов. Удобнее всего в качестве адресных переменных взять три старшие переменные нашей функции, т.е. a, b, c. Тогда пары наборов, на которых эти переменные будут иметь одинаковое значение, будут располагаться в соседних строчках таблицы истинности и поэтому можно будет легко увидеть, как значение логической функции для каждой пары наборов соотносится со значением переменной d (рисунок. 1). Например, из рисунок. 1 видно, что для первых двух строчек 𝐹 = 𝑑. Всего же для разных пар наборов может быть четыре случая: F = 1, F = 0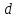, F = , 𝐹 = 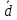. Таким образом, мы перенесли одну переменную в область значений функции и получили таблицу, похожую на таблицу истинности функции от трех переменных.

    Таблица 2 отображает «сжатую» таблицу истинности.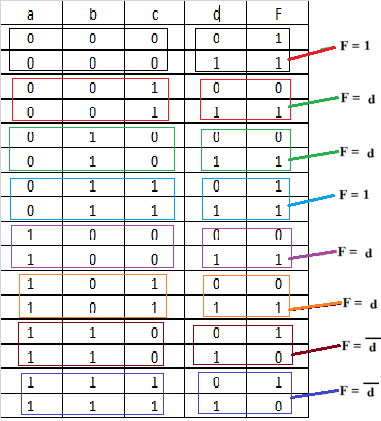



    Таблица. 3 Взаимосвязь значений функции и значений переменной «d»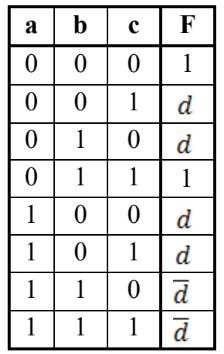



    Теперь, рассматривая переменную d наравне с константами 0 и 1 в качестве сигналов для информационных входов мультиплексора 8-1, можно по аналогии с предыдущим случаем выполнить реализацию требуемой функции. Разместим на рабочей области новый мультиплексор, установим ему количество выбирающих (адресных) входов равным трем, и выполним необходимые соединения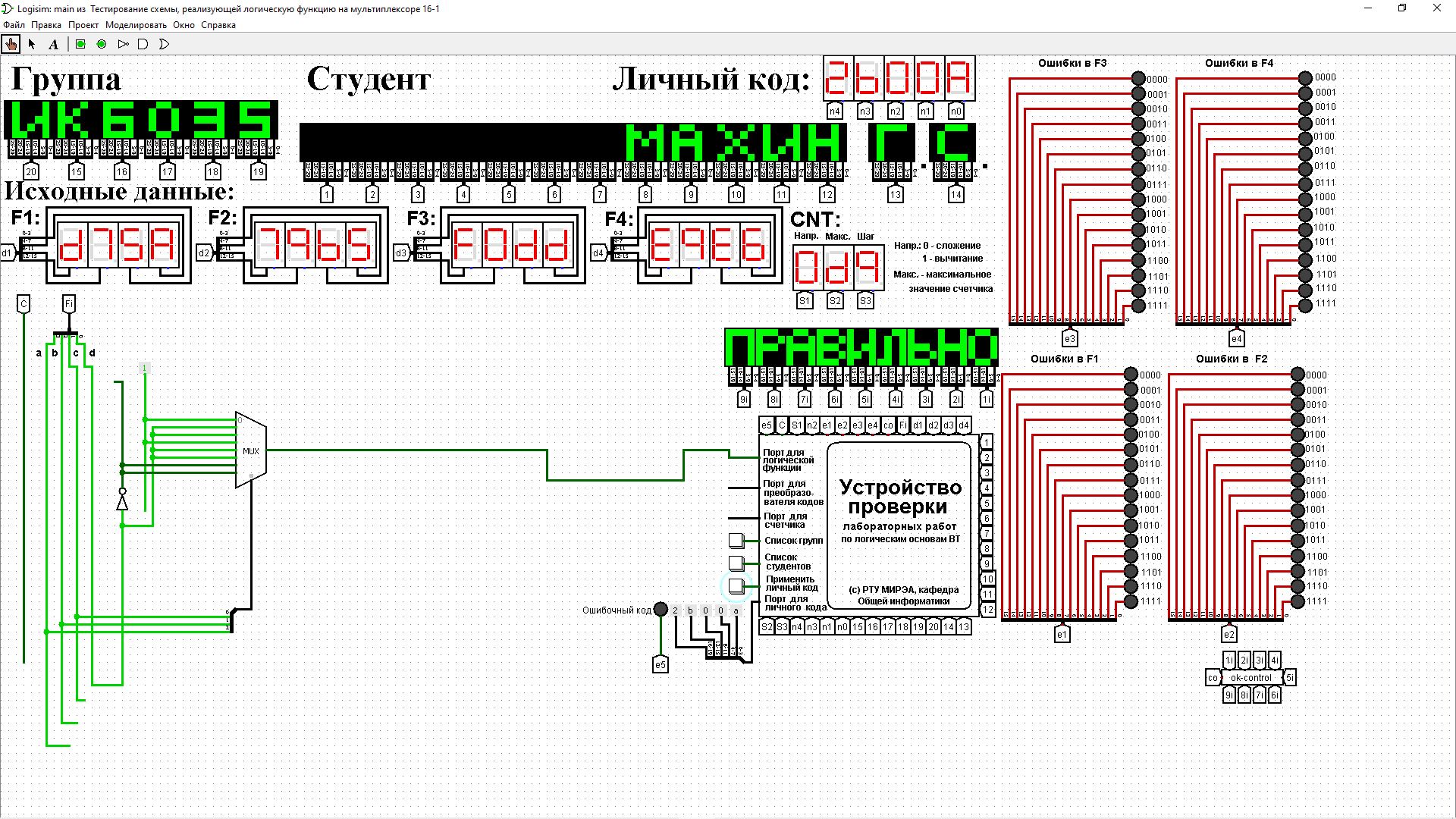



    Рисунок. 3 Тестирование схемы, реализующей логическую функцию на мультиплексоре 8-1

    Тестирование подтвердило правильность работы схемы.

    Рассмотрим реализацию заданной функции на минимальном количестве мультиплексоров 4-1.

    Мультиплексор 4-1 имеет 2 адресных входа и 4 информационных. Это означает, что мы должны разбить исходную таблицу истинности на 4 фрагмента, за реализацию каждого из которых в принципе должен отвечать отдельный мультиплексор (назовем его операционным). Однако, необходимо учесть требования минимальности по отношению к количеству используемых мультиплексоров и ставить их только там, где без них нельзя обойтись. Также нам нельзя в рамках данной работы использовать другие логические схемы, за исключением отрицания.

    По аналогии с реализацией на дешифраторах 2-4 (см. предыдущую работу), нам обязательно потребуется управляющий мультиплексор, который будет выбирать один из вариантов, предлагаемых операционными мультиплексорами (либо один из очевидных вариантов, если без операционных мультиплексоров можно обойтись).

    Разобьем исходную таблицу истинности на зоны ответственности между операционными мультиплексорами, а заодно посмотрим, нельзя ли в некоторых случаях обойтись вообще без операционного мультиплексора (рисунок. 4).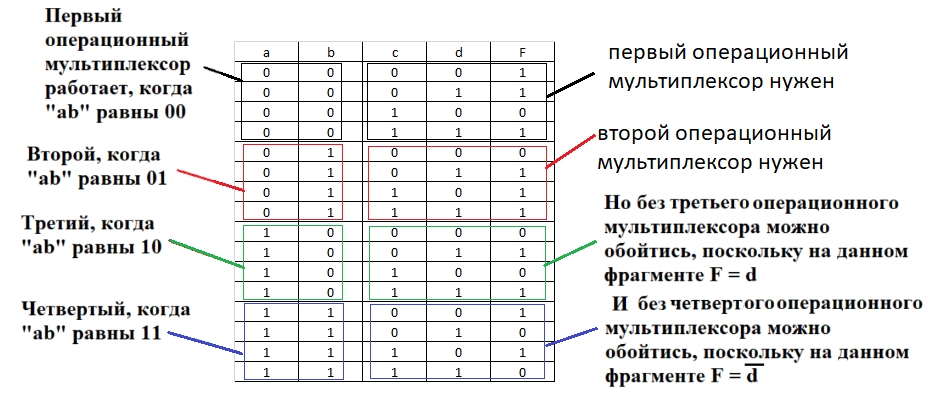



    Рисунок. 4 Разбиение исходной таблицы истинности на зоны ответственности для

    потенциальных операционных мультиплексоров

    С учетом того, что в некоторых случаях без мультиплексора можно обойтись, схема логической функции на минимальном количестве мультиплексоров 4-1 будет такой, как показано на рисунке. 5.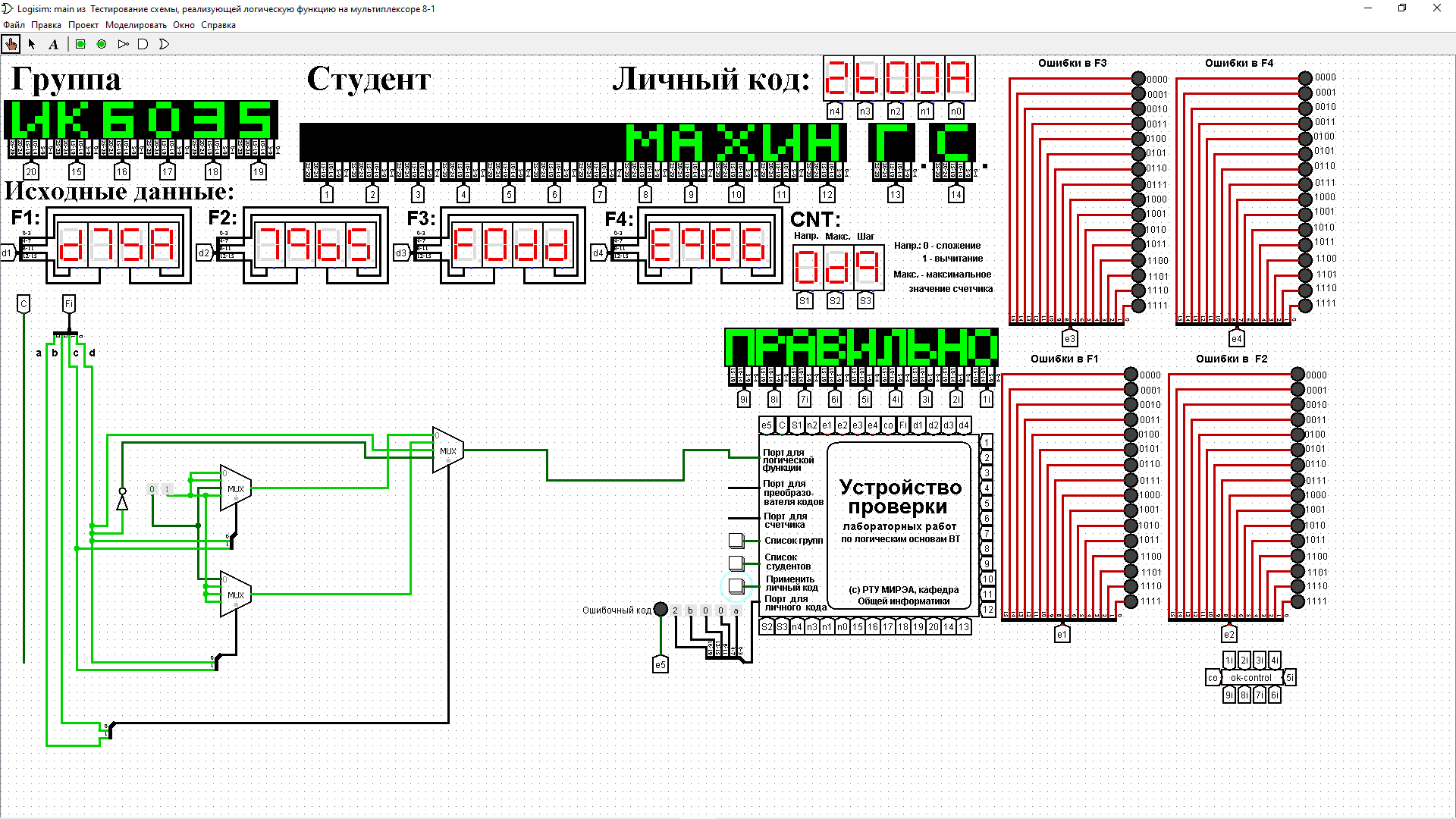



    Рисунок. 5 Тестирование схемы, реализующей логическую функцию на минимальном количестве мультиплексоров 4-1

    Реализуем логическую функцию, используя минимальную комбинацию мультиплексоров 4-1 и 2-1. В качестве отправной точки рассмотрим результаты, полученные в предыдущей реализации. Управляющий мультиплексор нельзя заменить на мультиплексор 2-1, поскольку у него на входах уникальные сигналы, а вот операционный заменить можно, поскольку он имеет дело с константами. Из рис. 4 выпишем отдельно фрагменты таблицы истинности, за который данные мультиплексоры отвечают (табл. 4,5).

    Таблица 4

    c
    d
    F

    0
    0
    1

    0
    1
    1

    1
    0
    0

    1
    1
    1


    Таблица 5

    c
    d
    F

    0
    0
    0

    0
    1
    1

    1
    0
    1

    1
    1
    1

    Из таблицы. 4 видно, что когда «с» равно 0, то функция равна не 1 , а когда «с» равно 1, то функция равна «d» . Значит, переменную «с» можно рассматривать как адресную для мультиплексора 2-1, а не 1 и «d» будут поданы на его информационные входы.

    Из таблицы 5 видно, что когда «с» равно 0, то функция равна не «d» , а когда «с» равно 1, то функция равна 1. Значит, переменную «с» можно рассматривать как адресную для мультиплексора 2-1, а не «d» и 1 будут поданы на его информационные входы. В результате получим схему, изображенную на рисунке. 6.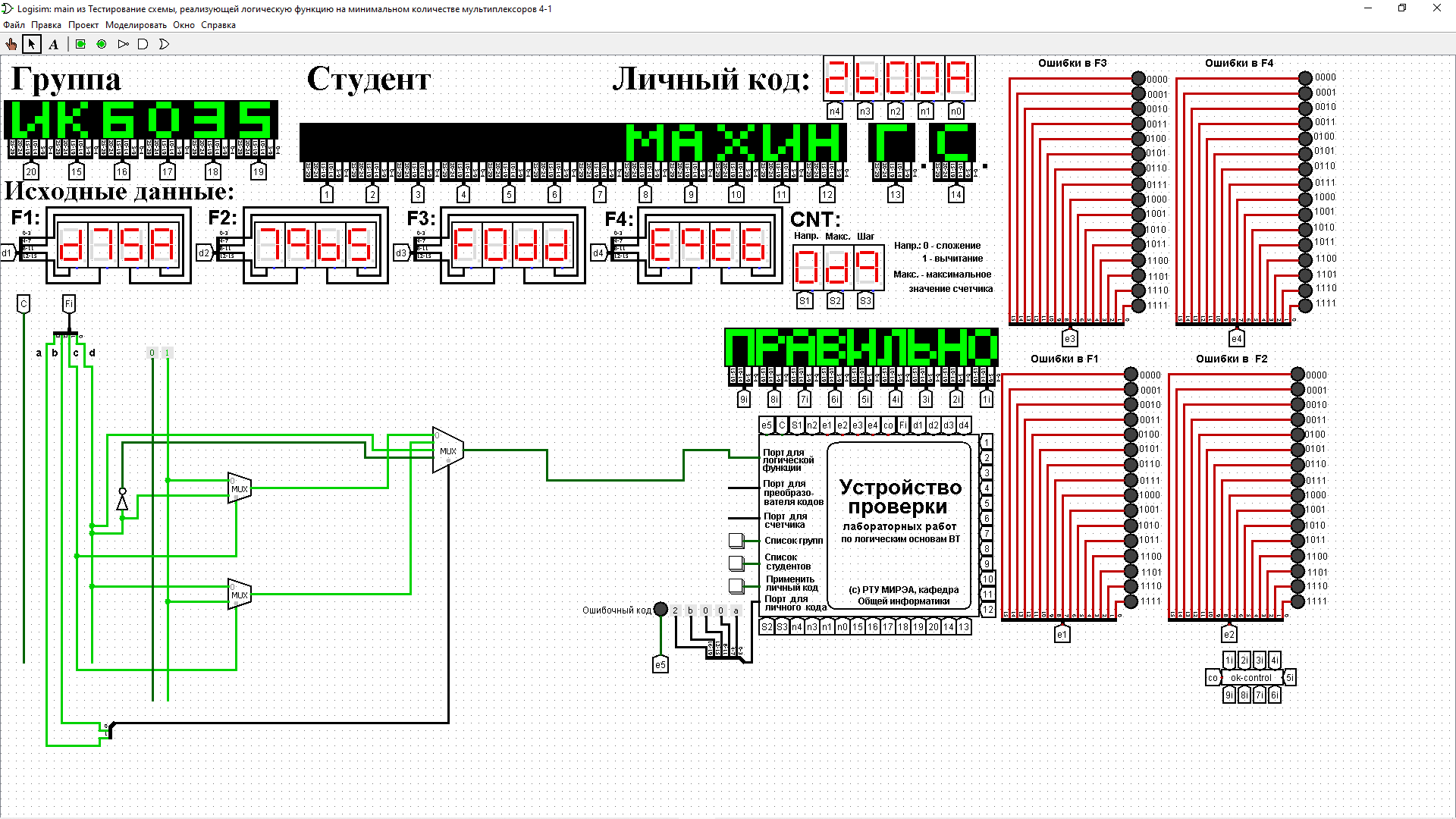



    Рисунок.6 Тестирование схемы, реализующей логическую функцию на основе минимальной комбинации мультиплексоров 4-1 и 2-1

    Тестирование подтвердило правильность работы схемы.

























    3. ВЫВОДЫ


    Была восстановлена таблица истинности. По таблице истинности реализована в лабораторном комплексе логическая функция на дешифраторах тремя

    способами:

    – используя дешифратор 4-16 и одну дополнительную схему «или»;

    – используя два дешифратора 3-8 и необходимую дополнительную логику;

    – используя пять дешифраторов 2-4 и одну дополнительную схему «или».

    4. ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ


    1.Смирнов С.С., Карпов Д.А. Методические указания по выполнению практических работ /, МИРЭА — Российский технологический университет/ М. 2020. – 102 с., Электронное издание.

    2.Лекции по информатике. Воронов Г.Б. РТУ МИРЭА. - Москва. 2021

    3.ГОСТ 7.25-2001 СИБИД. Тезарус информационно-поисковый одноязычный., Правила разработки, структура, состав и форма представления. – М. 2002. – 16 с., Электронное издание.

    4.Программа построения и моделирования логических схем Logisim.: Официальный сайт. URL: http://www.cburch.com/logisim Текст: электронный

    написать администратору сайта