ПОСТРОЕНИЕ АДДИТИВНОЙ МОДЕЛИ. Аддитивная. Отчет защищен с оценкой преподаватель доцент
 Скачать 1.91 Mb. Скачать 1.91 Mb.
|
|
ГУАП ФПТИ ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2021 Вариант 4 Условие: Компания «Авторусь» занимается поставками автозапчастей. Преимущества корпоративных клиентов начинаются с доставки – если в городе имеется представительство поставщика, она не будет стоить покупателю ни копейки. А также индивидуальный подход к каждому клиенту, гибкая система скидок и способов оплаты позволяет выбрать оптимальные условия прибыльного сотрудничества. За последние 11 кварталов товарооборот компании, скорректированный на инфляцию, составил:
Требуется: В предположении существования линейного тренда построить модель с аддитивной компонентой. Сделать прогноз на ближайшие три квартала. Прокомментировать вопрос о вероятной точности ваших прогнозов. Решение: Построение диаграммы временного ряда:
Таблица 1- «Квартальные объемы продаж компании «Авторусь»» Построим по этим данным гистограмму для более точного представления динамики изменения объёма продаж. 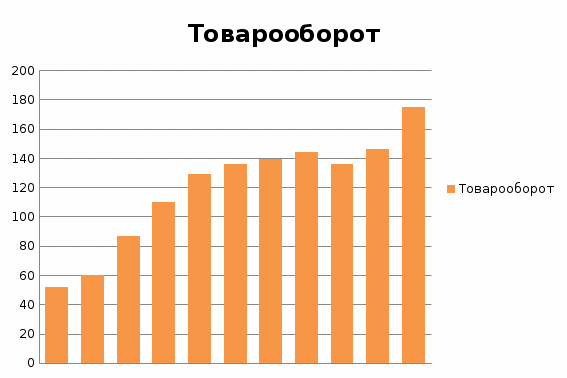 Рисунок 1 - Диаграмма временного ряда Объем продаж продукта подвержен сезонным колебаниям. К таким данным следует применять модель с аддитивной компонентой. В нашем примере есть все основания предположить существование линейного тренда, но чтобы полностью в этом убедиться, проведем процедуру сглаживания временного ряда. Анализ модели с аддитивной компонентой: A = T + S + E Аддитивная модель представляется как Фактическое значение = Трендовое значение + Сезонная вариация + Ошибка, т.е. A = T + S + E, где T – трендовая составляющая, S – сезонная составляющая, E – случайная составляющая (ошибка прогноза) Расчет сезонной компоненты методом скользящей средней (S). Общий результат вычислений коэффициентов сезонности представлен в виде таблицы (рисунок 2). 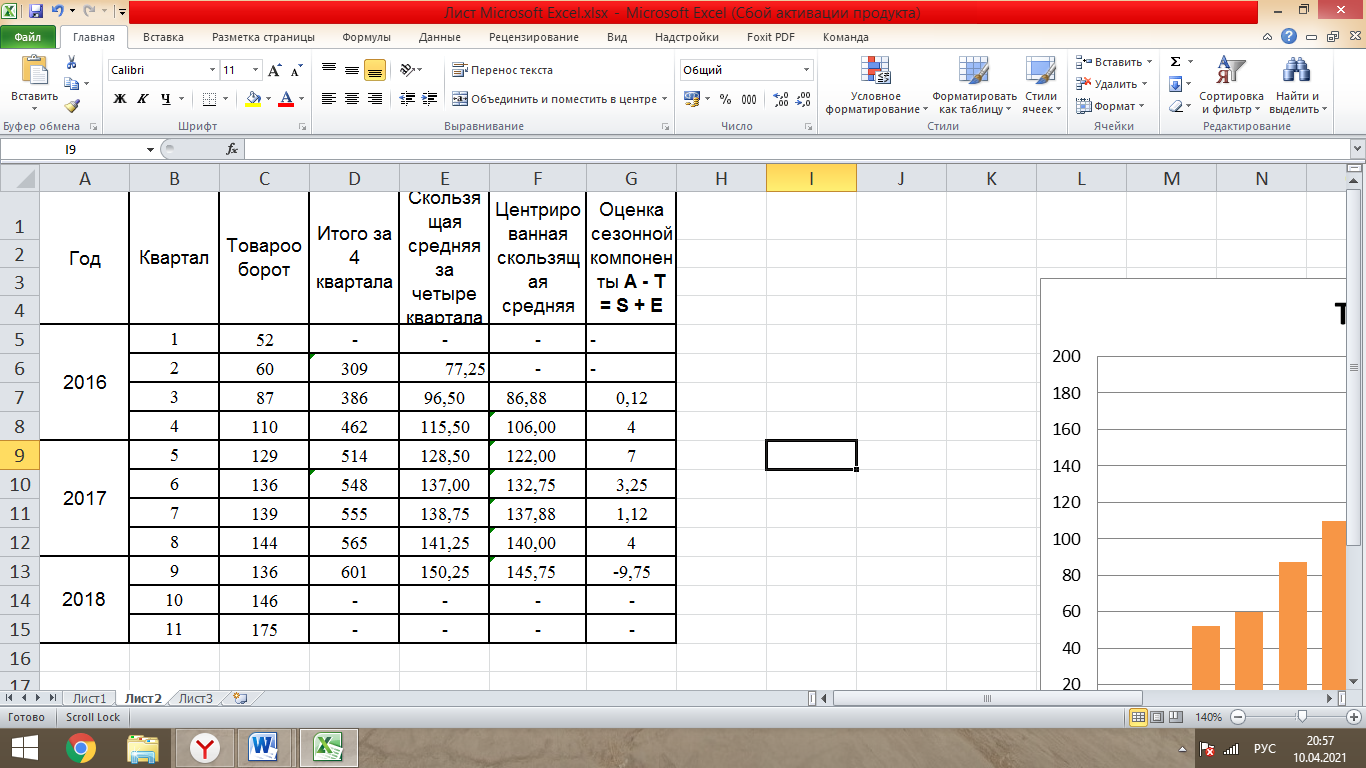 Рисунок 2 - «Результат вычислений коэффициентов сезонности» Таким образом, получили десезонализированную среднюю за каждый квартал (кроме 2-х начальных и конечных). Для каждого квартала мы имеем оценки сезонной компоненты, которые включают в себя ошибку или остаток. Прежде чем мы сможем использовать сезонную компоненту, нужно пройти два следующих этапа. Найдем средние значения сезонных оценок для каждого сезона года. Эта процедура позволит уменьшить некоторые значения ошибок. Наконец, скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы общая их сумма была равна нулю. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год. Для получения значений скорректированной сезонной компоненты необходимо рассчитать корректирующий коэффициент. Чтобы найти корректирующий коэфициент k, необходимо просуммировать среднюю оценку сезонной компоненты, а после поделить сумму на 4. Т.е. для данной модели имеем: k= 6,495 / 4= 1, 62375 Результат расчета скорректированной сезонной компоненты представлен в виде таблицы (рисунок 3). 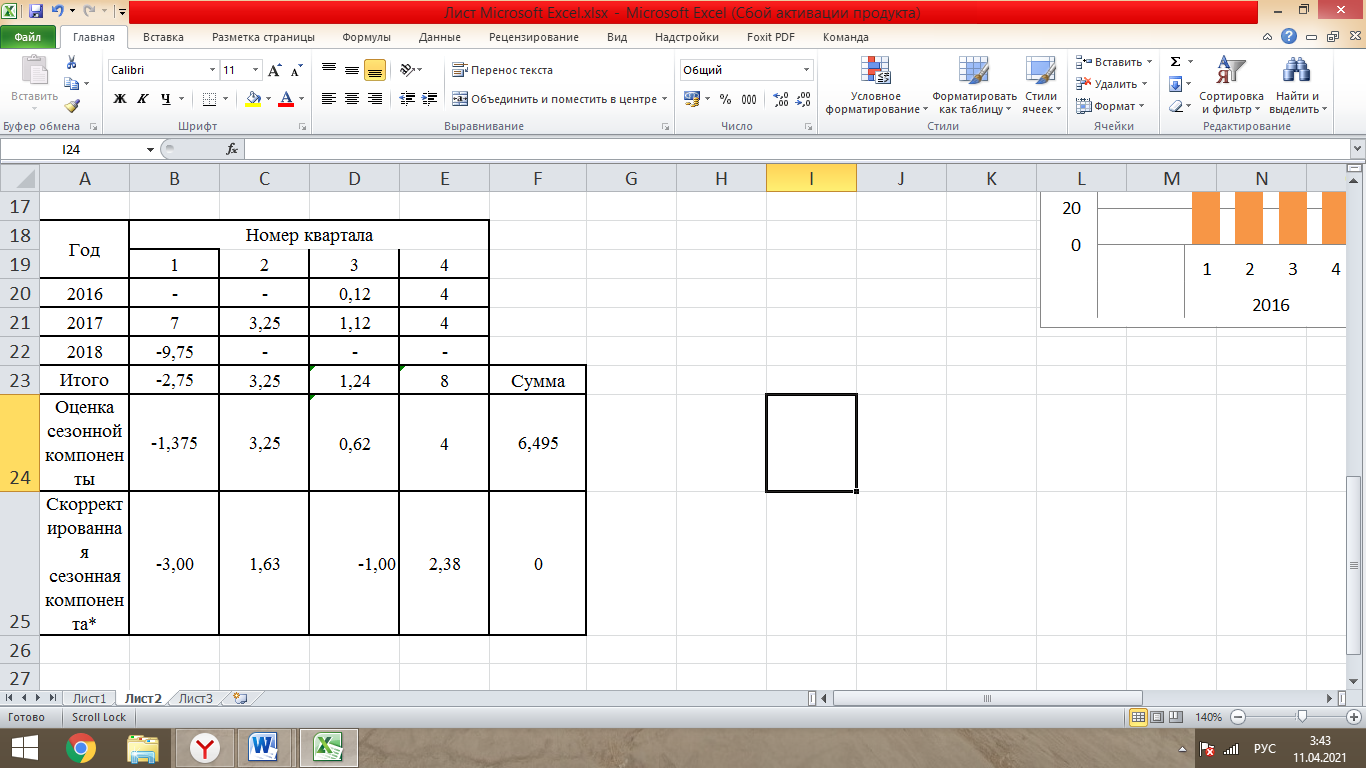 Рисунок 3 – «Результат расчета скорректированной сезонной компоненты» Десезонализация данныхПосле того как оценки сезонной компоненты определены, можем приступить к процедуре десезонализации данных по формуле A-S = T + E. Результат расчетов представлен в виде таблицы (рисунок 4). 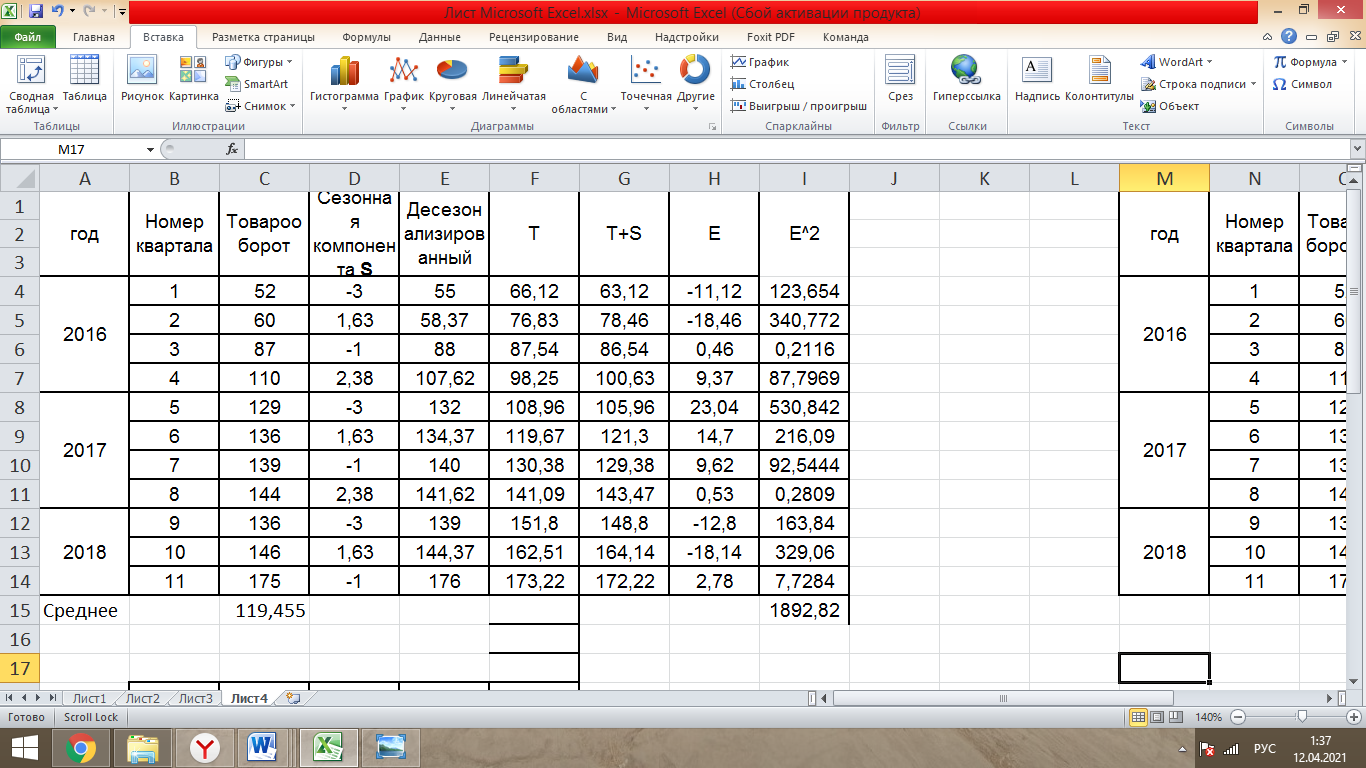 Рисунок 4 – «Результаты расчета десезонализированных данных» 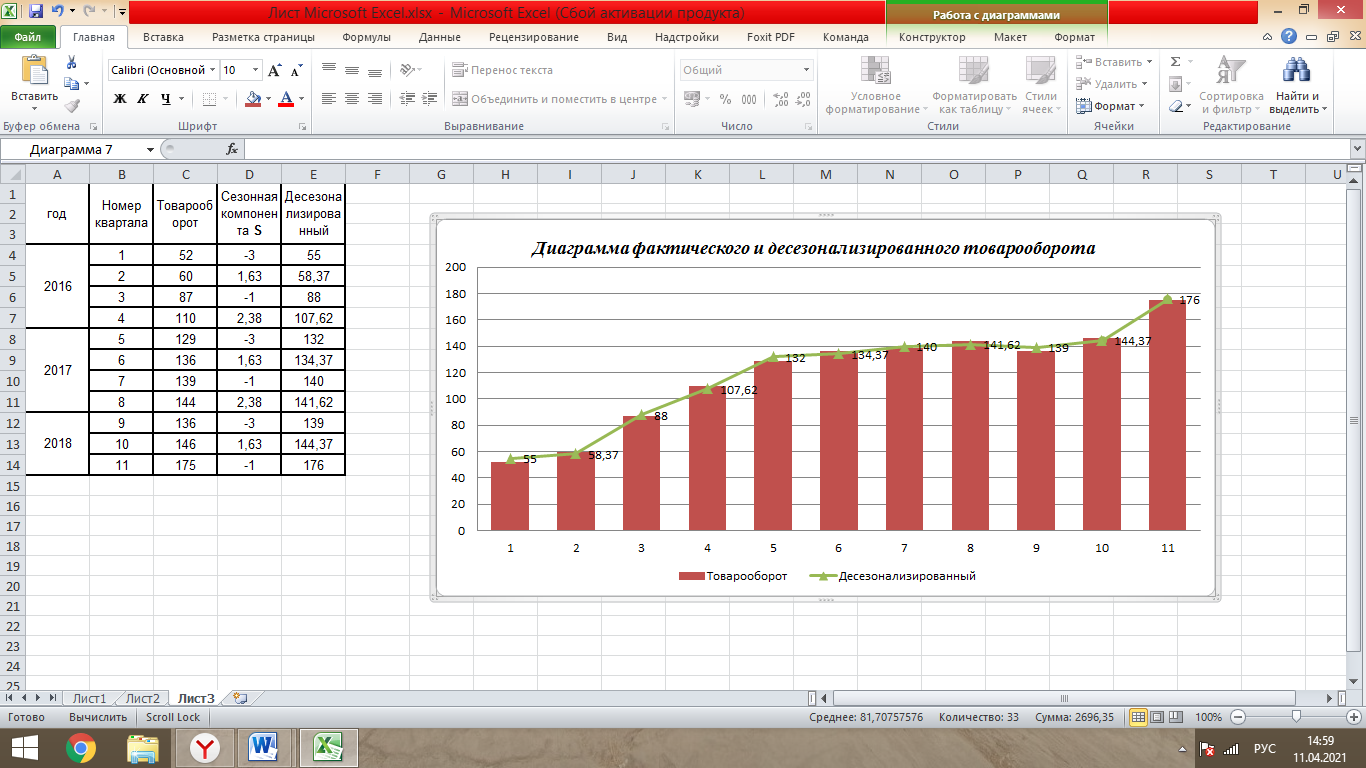 Рисунок 5 - Диаграмма фактического и десезонализированного товарооборота Из диаграммы видно, что во 1 и 3 квартале каждого года сезонная компонента влияет отрицательно на фактический объем продаж, а в 2 и 4 кварталах каждого года – положительно. Оценка значений тренда. Уравнение линии тренда имеет вид: T = a + b х – номер квартала, где a и b характеризуют точку пересечения с осью ординат и наклон линии тренда. Параметры a и b мы рассчитали с помощью встроенной функции Excel: ЛИНЕЙН.  Рисунок 6- расчет коэффициентов Следовательно, уравнение модели тренда имеет следующий вид: Трендовое значение объема продаж, тыс. шт. = 55,41 + 10,71х, где х – номер квартала. Из уравнения тренда видно, что с увеличением y на одну единицу х увеличивается на 10,71. Это уравнение будем использовать в дальнейшем для расчета оценок трендовых объемов продаж на каждый момент времени. Подставляя в уравнение модели тренда значения х = 1 ... 11 найдем Т для каждого момента времени. На рисунке 7 показан пример расчета трендового значения объема продаж. 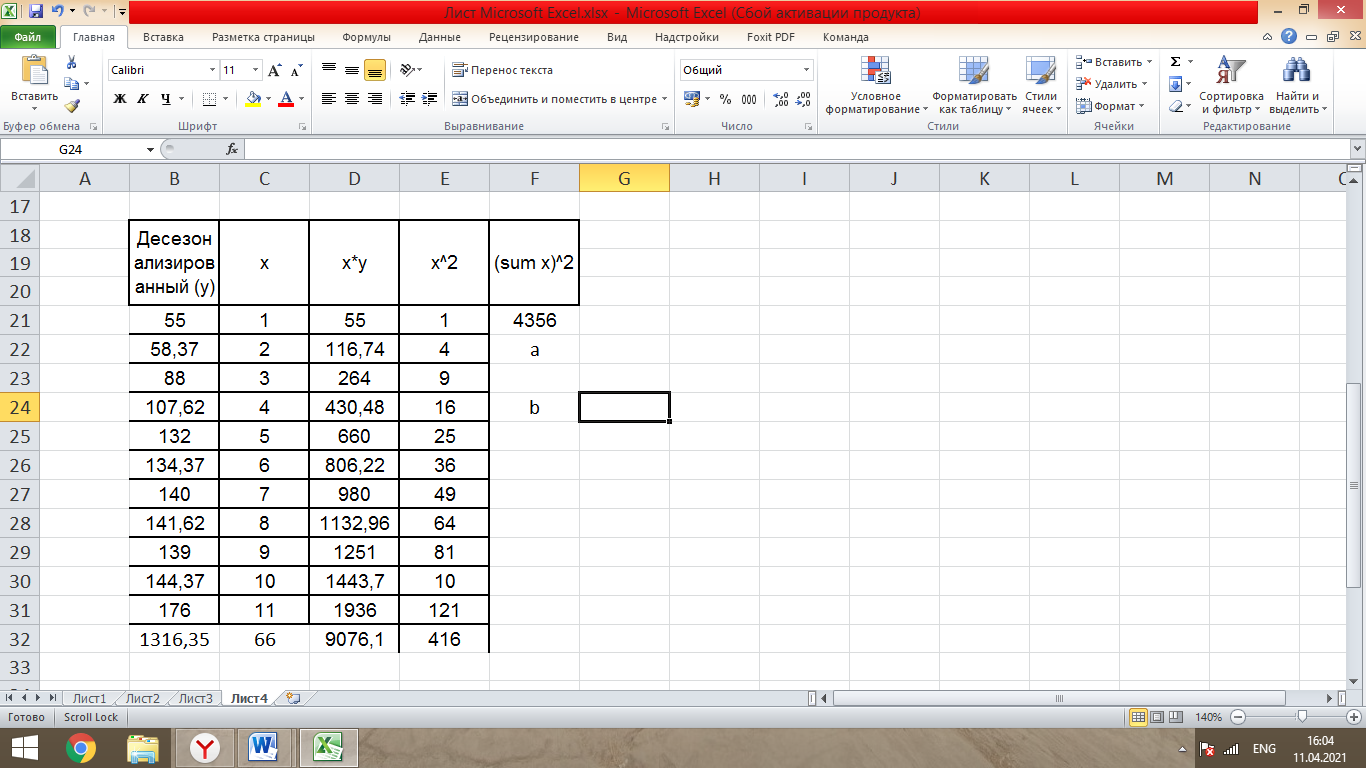 Рисунок 7 – «Пример расчета трендового значения объема продаж» Расчет ошибок Вычитая из фактического товарооборота значения тренда и сезонной составляющей можно найти значения ошибок. В колонке «Ошибка» = A - S – T, где А – товарооборот , S - Сезонная компонента, а T - Трендовое значение. Остальные данные копируются из таблиц, приведённых в предыдущих файла. Результат расчетов ошибок оформлен в виде таблицы 5 (рисунок 8). 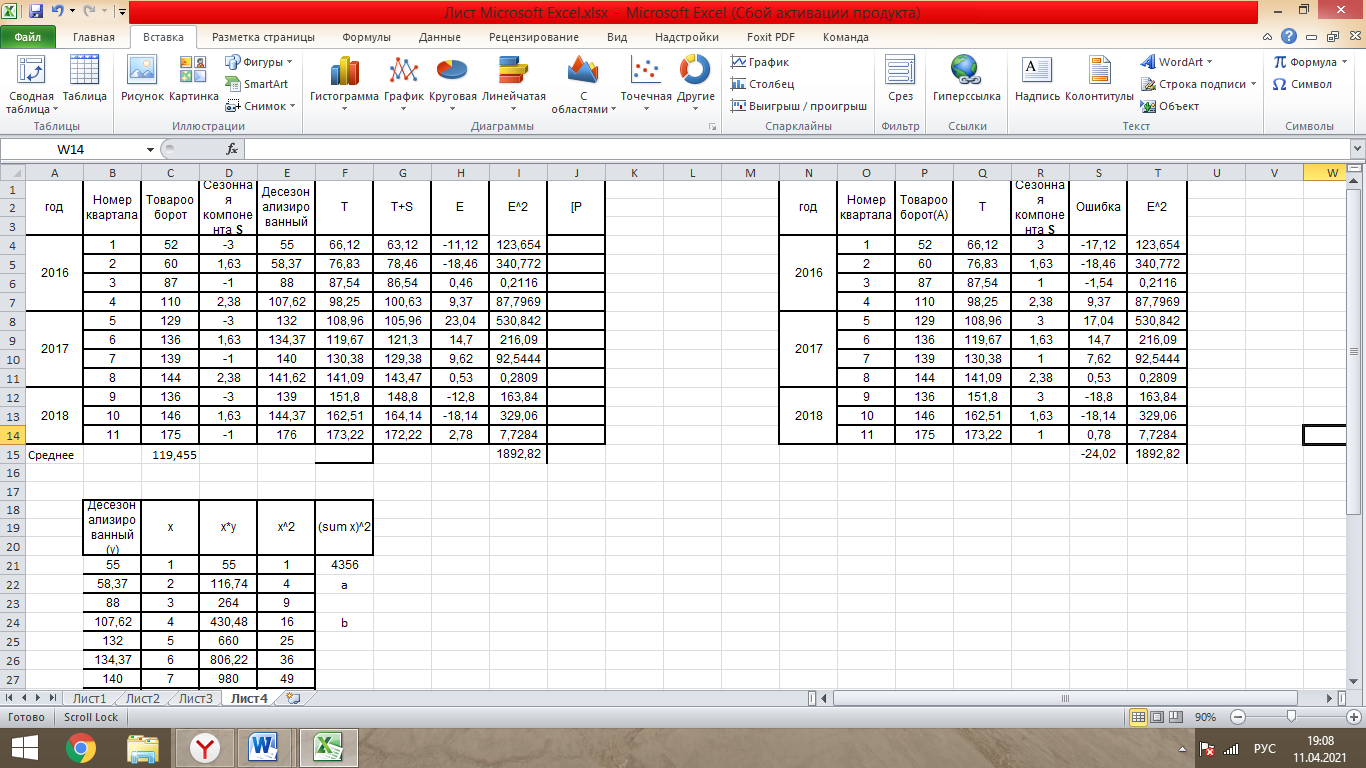 Рисунок 8 – «Расчет ошибок» Полученные данные можно использовать при расчете среднего абсолютного отклонения (MAD) или средней квадратической ошибки (MSE): 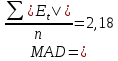 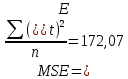 Для расчета MAD и MSE нужно взять ошибки, рассчитанные по формуле A – T - S = E. Тенденция, выявленная по фактическим данным, довольно устойчива и позволяет получить относительно верные краткосрочные прогнозы. Построим график, на котором отразим фактические данные, значения тренда, оценки (данные десезонализированного спроса). 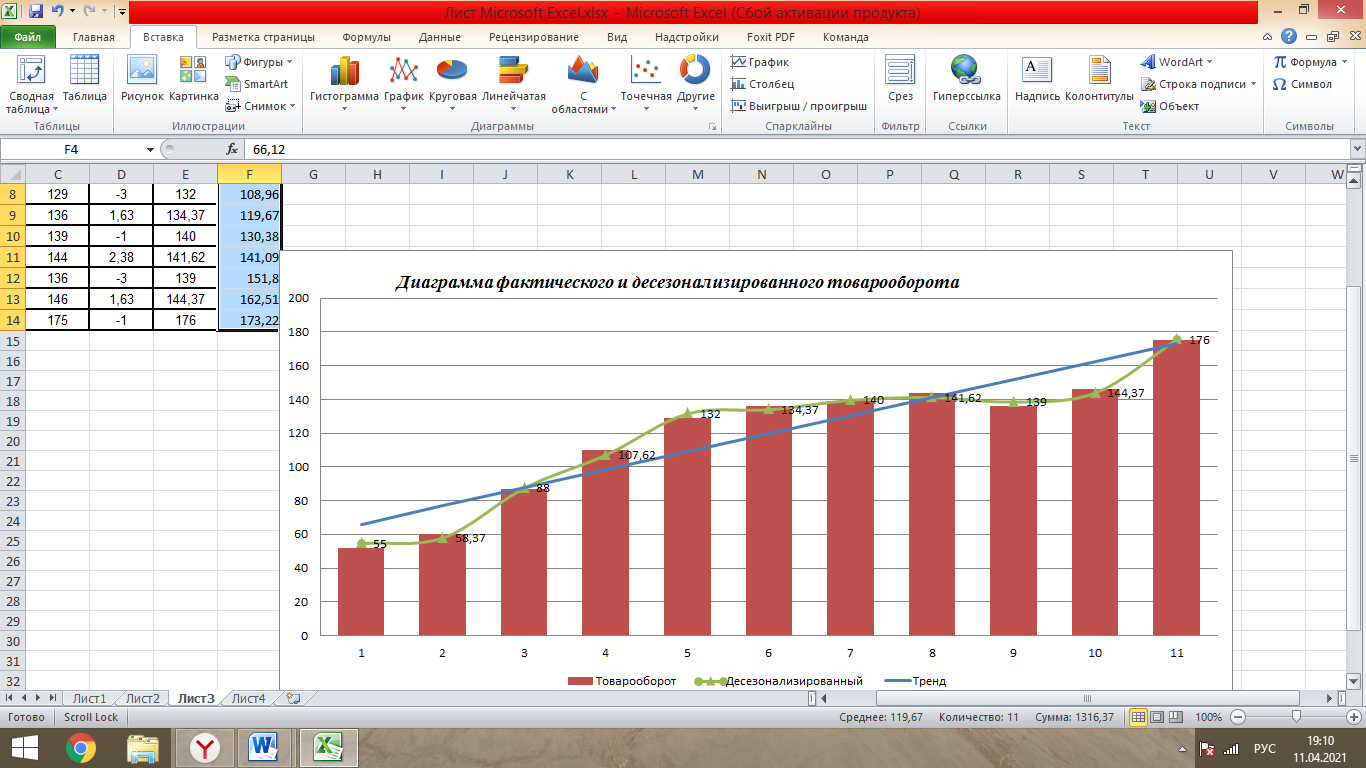 Рисунок 9 – Фактический объем, тренд, оценки Прогнозирование по аддитивной модели. Необходимо сделать прогноз на 12, 13, 14 кварталы. 4 квартал 2018 года, а так же 1 и 2 кварталы 2019 года. Для начала необходимо найти тренд для 12, 13, 14 кварталов. Расчеты представлены ниже. Т12=55,41 + 10,71*12 = 183,93; Т13=55,41 + 10,71*13 = 194,64; Т14=55,41 + 10,71*14 = 205,35 Значения сезонных компонент за соответствующие кварталы равны: S12= 2,38; S13= -3, S14=1,63. Таким образом, собрав все данные необходимо сделать прогноз на необходимые кварталы, расчет представлен ниже: F12=T12+S12=183,93+2,38= 186,31; F13=T13+S13=194,64+(-3)= 191,64; F14=T14+S14=205,35+1,63=206,98. Вывод: Согласно расчетам в 12,13 и 14 кварталах компании стоит ожидать повышение спроса. Построим график линейного, степенного и полиномиального тренда (Рисунки 10, 11, 12, 13). 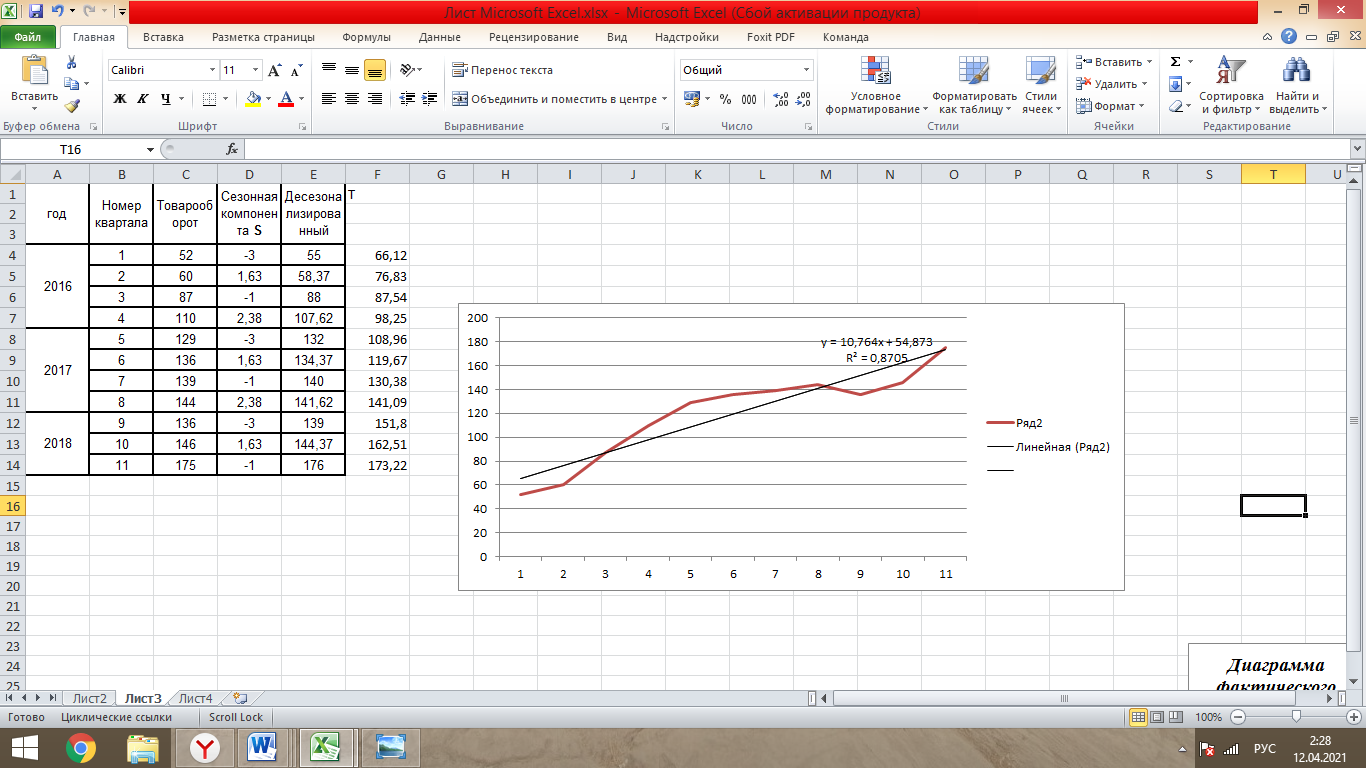 Рисунок 10 - «График с линейным трендом» 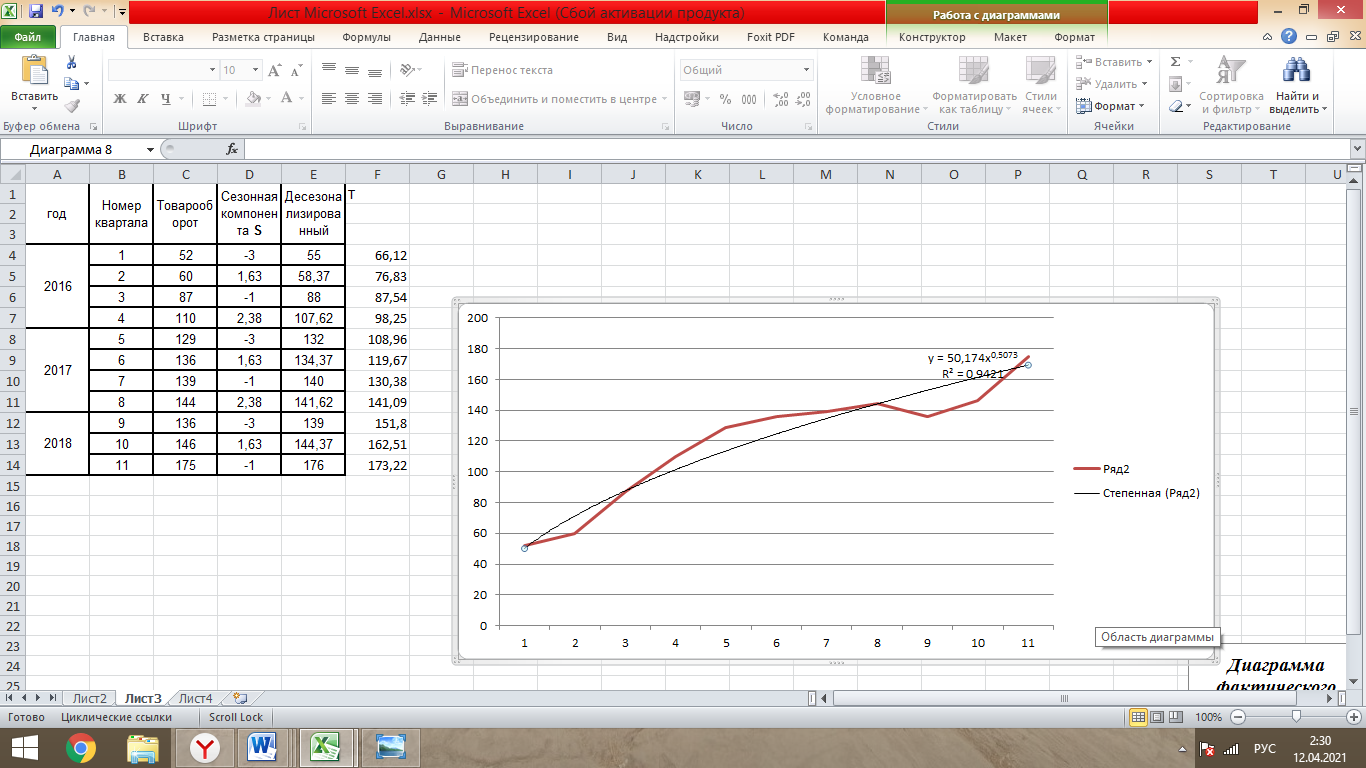 Рисунок 11 - «График со степенным трендом» 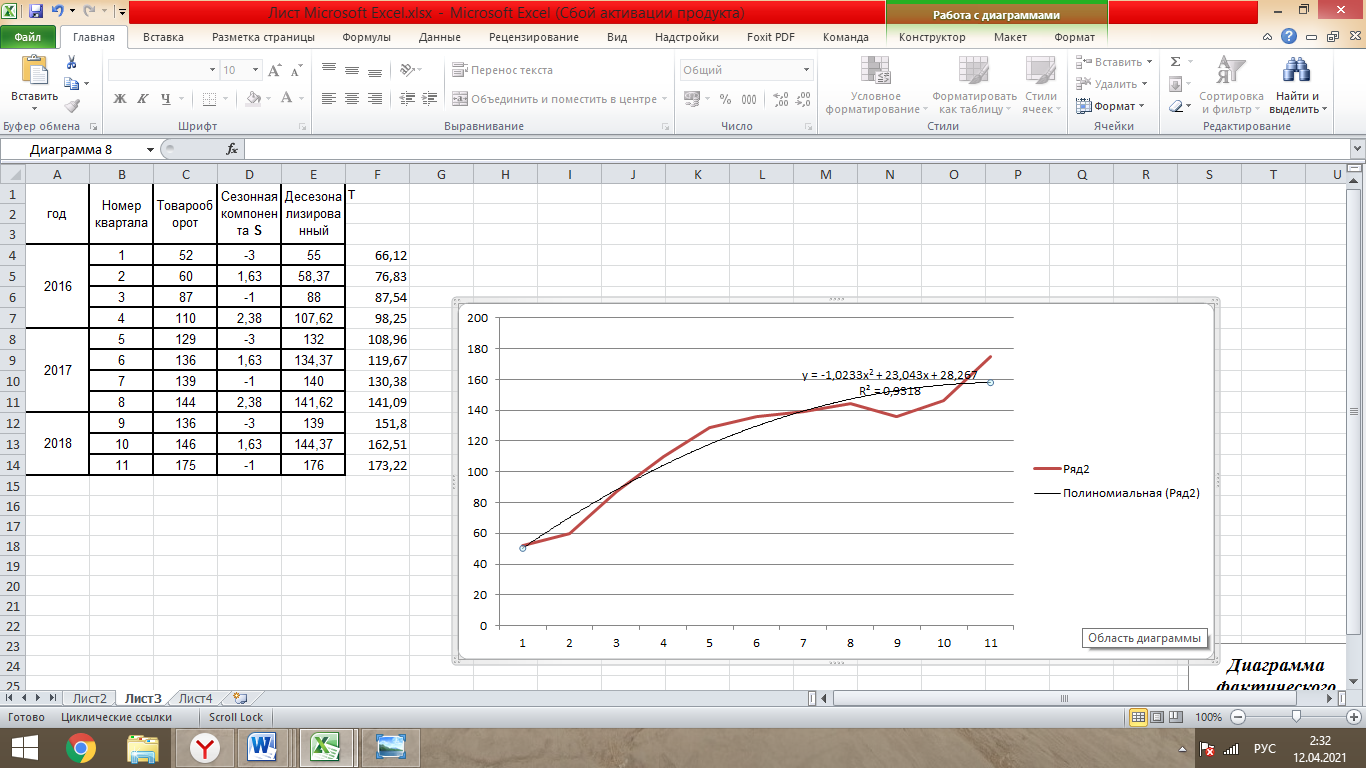 Рисунок 14 – «График с полиномиальным трендом 2й степени» Из графиков линейного, степенного и полиномиального трендов выявлены значения R2: линейный - R2=0,87; степенной - R2=0,94; полиномиальный 2-й степени - R2=0,93. Можно сделать вывод о том, что степенной тренд описывает лучше всего исходные данные – на 94 %. Расчет коэффициентовЛинейная регрессия и оценка ее параметров Уравнение линейной регрессии имеет вид: Yp=a+b*x Следовательно, уравнение линейной регрессии имеет следующий вид: Ур = 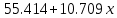 Из уравнения линейной регрессии видно, что с увеличением y на одну единицу, х увеличивается на 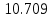 . .
Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера. При этом выдвигается нулевая гипотеза (Н0), которая говорит об отсутствии взаимосвязи между фактором и результатирующим признаком, т.е. об отсутствии статистической значимости уравнения регрессии. Н1 – альтернативная гипотеза, эта гипотеза говорит о существенности взаимосвязи между фактором и результатирующим признаком, т.е. об соответствии статистической значимости уравнения регрессии. Н0 применяется если F расч Н1 применяется если F расч> Fтабл Коэффициент корреляции(rxy) Коэффициент корреляции – это статистический показатель, показывающий, насколько связаны между собой колебания значений двух других показателей. Коэффициент корреляции может изменяться в пределах от -1 до +1. При этом, значение -1 будет говорить об отсутствии корреляции между величинами, 0 – о нулевой корреляции, а +1 – о полной корреляции величин. Т. е., чем ближе значение коэффициента корреляции к +1, тем сильнее связь между двумя случайными величинами. Расчет коэффициента корреляции для нашего примера будет следующим: 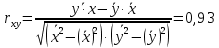 В нашем примере связь между признаком Y и фактором X весьма высокая и прямая. Коэффициент детерминации R2 Коэффициент детерминации – оценка качества («объясняющей способности») уравнения регрессии, за счет того, что будет показывать на сколько учтены все факторы. Коэффициент детерминации может принимать значения от 0 до 1. Чем ближе к 1 , тем лучше качество связи. Для модели линейной регрессии с одним признаком х коэффициент детерминации равен квадрату обычного коэффициента корреляции между х и у: 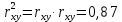 Коэффициент детерминации означает, что 87% вариации результирующего признака (y) объясняется вариацией фактора (х), а 13 % - неучтённые факторы. Это говорит о очень хорошей модели. Средняя ошибка аппроксимации  Средняя ошибка аппроксимации – оценка качества уравнения регрессии, которая показывает, на сколько процентов в среднем отличаются фактические значения результативного показателя у от значений 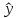 . .Значение ошибки аппроксимации до 10 % свидетельствует о высокой точности модели. Если величина средней ошибки аппроксимации попадает в диапазон от 10 до 20 %, то точность модели может быть признана хорошей. Величина ошибки в интервале от 20 до 50 % означает удовлетворительную точность подбора модели регрессии. 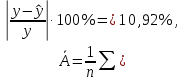 где 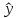 – значение результативного показателя, рассчитанное по уравнению парной регрессии. – значение результативного показателя, рассчитанное по уравнению парной регрессии. Средняя ошибка аппроксимации показала, что модель хороша, т. к. 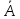 незначительно превышает 10 %. незначительно превышает 10 %.Эластичность 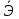 Коэффициент эластичности показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1 % от своей средней величины. 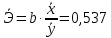 Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно. Вывод: В лабораторной работе была использована аддитивная модель, т.е. модель, в которую факторы входят в виде алгебраической суммы. Объем продаж продукта подвержен сезонным колебаниям. К таким данным следует применять модель с аддитивной компонентой. Из диаграммы видно, что во 1 и 3 квартале каждого года сезонная компонента влияет отрицательно на фактический объем продаж, а в 2 и 4 кварталах каждого года – положительно. Так же было выявлено что тенденция довольно устойчива и позволяет получить относительно верные краткосрочные прогнозы. Сделав прогноз на следующие три квартала, мы определили, что значения F в 12, 13 и 14 кварталах растут. Согласно расчетам в 12,13 и 14 кварталах компании стоит ожидать повышение спроса. Среднее абсолютное отклонение (MAD) составило 2,18 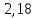 , а среднее квадратическая ошибка (MSE) составила 172,07. , а среднее квадратическая ошибка (MSE) составила 172,07.Прогнозные значения на 4 квартал 2018 года, а так же 1 и 2 кварталы 2019 года. F12= 186,31; F13=191,64; F14= 206,98. Коэффициент корреляции составил 0,93 – это показывает, что связь является прямопрапорциональной т.к. значение приближенно к 1, достаточно тесная связь. Коэффициент детерминации равен 0,87 , что говорит о том, что 87% влияющих на модель факторов было учтено, а 13% не учтено- хорошая модель. Теоретическое значение Y отличается от практического в среднем на 10,92%. А коэффициент эластичности показал, что с увеличением фактора х на 1 % от своего среднего значения, результат y увеличивается на 0,537%. |
