Ответы к экзамену по вышке
 Скачать 110.26 Kb. Скачать 110.26 Kb.
|
|
Ответы к экзамену по вышке Определитель первого порядка имеет вид det A = a1 Определитель второго порядка имеет вид det A = 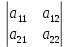 =a11 · a22 – a12 · a21. =a11 · a22 – a12 · a21.Определитель не изменится, если его строки заменить столбцами и наоборот. При перестановке двух параллельных рядов определитель меняет знак. Определитель, имеющий два одинаковых ряда равен нулю. Общий множитель элементов какого-нибудь ряда определителя можно вынести за знак определителя. Если элементы какого-либо ряда определителя представляют собой сумы двух слагаемых, то определитель может быть разложен на суму двух соответствующих определителей. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число. Определитель равен суме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида 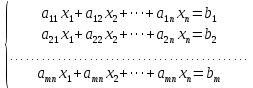 где числа aij, i= 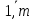 , j= , j=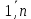 называются коэффициентами системы, числа bi ― свободными членами. называются коэффициентами системы, числа bi ― свободными членами.Такую систему можно записать в метрической форме А · Х = В Здесь А ― матрица коэффициентов системы, называемая основной матрицей. Х ― вектор-столбец из неизвестных xj. В ― вектор-столбец из свободных членов bi.  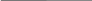  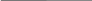 Формула Крамера 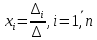 Вектор ― это направленный прямолинейный отрезок, т.е. отрезок, имеющий определённую длину и определённое направление. Если А ― начало вектора, а В ― его конец, то вектор обозначается символом 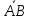 или или 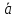 . Векторы отличающиеся только знаками называются противоположными. Коллинеарными векторами называются векторы, которые лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору. Два вектора называются равными, если они коллинеарные, одинаково направленные и имеют одинаковую длину. Вектор, длина которого равна единицы, называется единичным вектором и обозначается . Векторы отличающиеся только знаками называются противоположными. Коллинеарными векторами называются векторы, которые лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору. Два вектора называются равными, если они коллинеарные, одинаково направленные и имеют одинаковую длину. Вектор, длина которого равна единицы, называется единичным вектором и обозначается 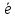 . .Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число. Сложение и вычитание векторов происходит по правилам треугольника и параллелограмма. Произведение вектора на число называется вектор 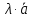 , который имеет длину , который имеет длину 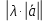 , коллинеарен вектору , коллинеарен вектору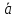 , имеет направление вектора , имеет направление вектора 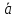 , если , если 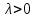 и противоположное направление, если и противоположное направление, если  Матрицей называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрицы равны между собой, если равны все соответствующие элементы этих матриц. Квадратной матрицей называется матрица, у которой одинаковое число столбцов и строк. Диагональной матрицей называется квадратная матрица, у которой все элементы равны нулю, кроме главной диагонали. Единичной матрицей называется квадратная матрица, у которой каждый элементы главной диагонали равен единицы. Над матрицами можно совершать такие действия как сложение, умножение матрицы на число, умножать матрицу на матрицу, а также совершать элементарные преобразования ( перестановка местами двух параллельных рядов матрицы, умножение всех элементов ряда на число отличное от нуля, прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число). Всякая невырожденная матрица имеет обратную. Формула для нахождения обратной матрицы 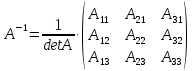 Свойства обратной матрицы  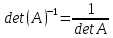  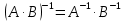  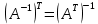 1.1 найти ранги основной и расширенной матриц системы. Если 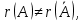 то система не совместима. то система не совместима. 2.1 если система совместима, то нужно найти какой-либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор называют главными и оставляют слева, а остальные n-r известных называют свободными и переносят в правые части уравнений. 2.1 если система совместима, то нужно найти какой-либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор называют главными и оставляют слева, а остальные n-r известных называют свободными и переносят в правые части уравнений.  1.3 найти выражения главных неизвестных через свободные. 1.3 найти выражения главных неизвестных через свободные.1.4 предавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений. Несобственный интеграл второго рода 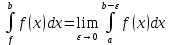 Если придел в правой части существует, то несобственный интеграл сходится, а если же указанный придел не существует или бесконечен, то интеграл расходится (в точке х=b) В точке х=b 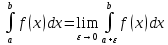 Если функция имеет разрыв внутри отрезка [a;b], то несобственный интеграл второго рода определяется формулой 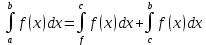 Интеграл 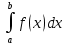 в геометрическом смысле равен площади бесконечно высокой криволинейной трапеции. в геометрическом смысле равен площади бесконечно высокой криволинейной трапеции.Теорема Кронекера-Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ран расширенной матрицы системы равен рангу основной матрицы. Угол между прямыми 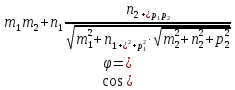 или или 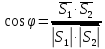 Если прямые перпендикулярны, то в этом и только в этом случае 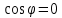 . Следовательно, числитель дроби равен нулю, т.е. m1m2+n1n2+p1p2=0 . Следовательно, числитель дроби равен нулю, т.е. m1m2+n1n2+p1p2=0Если прямые параллельны, то параллельны их направляющие векторы. Следовательно, координаты этих векторов пропорциональны, т.е. 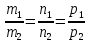 Прямые лежат в одной плоскости, если векторы 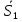 , , 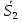 и и 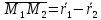 компланарны. Условием компланарности векторов является равенству нулю их смешанного произведения. компланарны. Условием компланарности векторов является равенству нулю их смешанного произведения.Несобственный интеграл первого рода 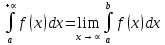 Если существует конечный придел, то интеграл сходится, а если такой придел не существует или он бесконечен, то интеграл не сходится. Аналогично определяется несобственный интеграл на промежутке [- 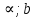 ]. Если интеграл сходится, то он равен площади бесконечно длинной криволинейной трапеции. ]. Если интеграл сходится, то он равен площади бесконечно длинной криволинейной трапеции.Формула Ньютона-Лейбница 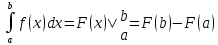 Скалярное произведение двух нулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. 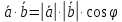 Свойства скалярного произведения  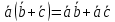  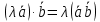 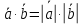 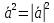 Выражение через координаты
 Векторным произведением вектора 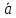 на вектор на вектор 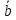 называется вектор называется вектор 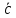 , который перпендикулярен векторам , который перпендикулярен векторам 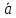 и и 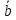 , имеет длину, численно равную площади параллелограмма, построенного на векторах , имеет длину, численно равную площади параллелограмма, построенного на векторах 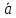 и и 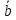 . . 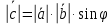 Свойства векторного произведения 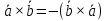 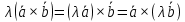 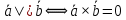 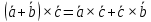 Выражение векторного произведения через координаты
Смешанным произведение векторов называется произведение, в котором два первые вектора перемножаются векторно, а третий скалярно на их результат. Свойства смешанного произведения 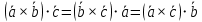 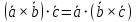 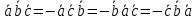 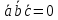 ― векторы ― векторы 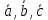 ― компланарны. ― компланарны.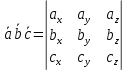 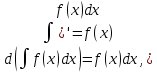 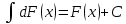 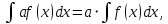 a a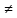 0 ― постоянная 0 ― постоянная 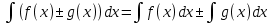 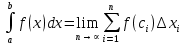 Теорема Коши: если функция 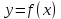 не прерывная на отрезке [a;b], то определённый интеграл не прерывная на отрезке [a;b], то определённый интеграл 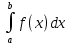 существует существуетОпределённый интеграл не зависит от обозначения переменной интегрирования  Определённый интеграл с одинаковыми приделами интегрирования равен нулю 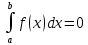 Для любого действительного числа c:  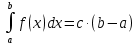 Угол между прямыми 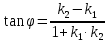 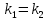 ― условие параллельности прямых. ― условие параллельности прямых.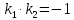 ― условие перпендикулярности прямых. ― условие перпендикулярности прямых.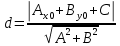 Функция 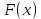 называется первообразной функции называется первообразной функции 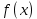 на интервале на интервале 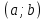 , если для любого , если для любого 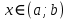 выполняется равенство выполняется равенство 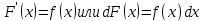 Если функция 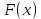 является первообразной функции является первообразной функции 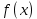 на на 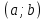 , то множество всех первообразных для , то множество всех первообразных для 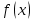 задаётся формулой задаётся формулой 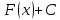 , где С ― постоянное число. , где С ― постоянное число.Неопределённым интегралом от функции 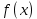 называется множество всех первообразных функций называется множество всех первообразных функций 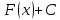 и обозначается и обозначается  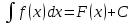 Комплексным числом 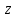 называется выражение называется выражение 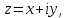 где х и у ― действительные числа, а і ― так называемая мнимая единица, i2 = -1. Если х=0, то число 0+iy называется мнимым. Число х называется действительной часть комплексного числа z и обозначается x= Re z, a y ― мнимой частью z, y= Im z. Комплексные числа равны тогда, когда равны их действительные и мнимые части. Ось абсцисс называется действительной осью, а ось ординат мнимой. где х и у ― действительные числа, а і ― так называемая мнимая единица, i2 = -1. Если х=0, то число 0+iy называется мнимым. Число х называется действительной часть комплексного числа z и обозначается x= Re z, a y ― мнимой частью z, y= Im z. Комплексные числа равны тогда, когда равны их действительные и мнимые части. Ось абсцисс называется действительной осью, а ось ординат мнимой. 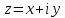 называют алгебраической формой комплексного числа, а называют алгебраической формой комплексного числа, а 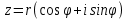 тригонометрической формой. тригонометрической формой.Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, больше чем расстояние между фокусами. Вывод канонического уравнения эллипса Согласно определению эллипса 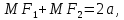 т.е. т.е.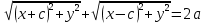 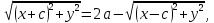 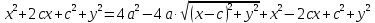 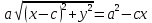 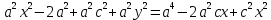 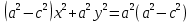 Так как 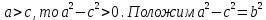 Тогда последние уравнение примет вид 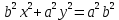 или или 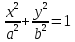 ― каноническое уравнение эллипса. ― каноническое уравнение эллипса.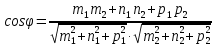 ― угол между прямыми в пространстве ― угол между прямыми в пространстве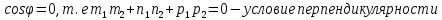 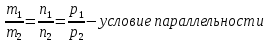 Прямые лежат в одной плоскости, если векторы 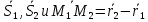 компланарны. компланарны.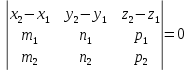 ― условие компланарности векторов ― условие компланарности векторов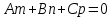 ― условие параллельности прямой и плоскости в пространстве ― условие параллельности прямой и плоскости в пространстве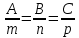 ― условие перпендикулярности плоскости и прямой ― условие перпендикулярности плоскости и прямой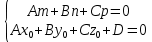 ―условие принадлежности прямой к плоскости ―условие принадлежности прямой к плоскостиПолярная система координат ― это система координат которая задаётся точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором 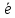 того же направления, что и луч Ор. Отсчёт углов идёт против часовой стрелки. Полярными координатами называют того же направления, что и луч Ор. Отсчёт углов идёт против часовой стрелки. Полярными координатами называют 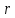 и и 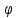 , при это rназывают полярным радиусом, а , при это rназывают полярным радиусом, а 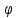 ― полярным углом. ― полярным углом. 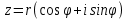 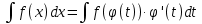 ― метод подстановки ― метод подстановки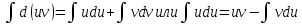 Всякое комплексное число  можно изобразить точкой М (х; у) плоскости Оху такой, что x=Re z, y= Im z, и наоборот каждую точку М(x; y) координатной плоскости, как образ комплексного числа можно изобразить точкой М (х; у) плоскости Оху такой, что x=Re z, y= Im z, и наоборот каждую точку М(x; y) координатной плоскости, как образ комплексного числа  . Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=x+0i=x, а ось ординат мнимой, так как на ней лежат чисто мнимые комплексные числа z=0+iy. . Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=x+0i=x, а ось ординат мнимой, так как на ней лежат чисто мнимые комплексные числа z=0+iy.График дифференцируемой функции у=f(x) называется выпуклым вниз на интервале (a;b), если он расположен выше любой касательной на это интервале. График функции у=f(x) называется выпуклым вверх на интервале 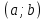 , если он расположен ниже любой её касательной на данном интервале. Точка графика непрерывной у=f(x), отделяющая его части разной выпуклости, называется точкой перегиба. , если он расположен ниже любой её касательной на данном интервале. Точка графика непрерывной у=f(x), отделяющая его части разной выпуклости, называется точкой перегиба. 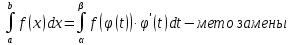  Нахождение площади     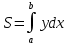 , , 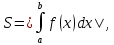 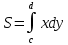 , , 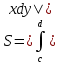           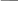 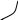     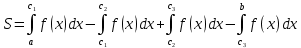  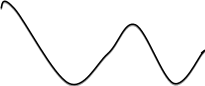      Число 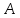 называется приделом функции в точке называется приделом функции в точке 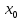 (или при (или при 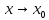 ), если для любого положительного ), если для любого положительного 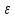 найдётся такое положительное число найдётся такое положительное число 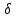 , что для всех , что для всех 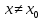 , удовлетворяющих неравенству , удовлетворяющих неравенству 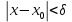 , выполняется неравенство , выполняется неравенство 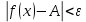 . Записывают . Записывают 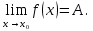 Это определение можно записать коротко так Это определение можно записать коротко так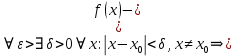 придел с лева придел с лева  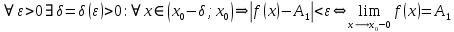 или коротко или коротко 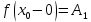 придел справа 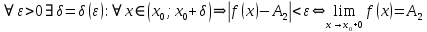 или коротко 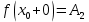 Приделы функции слева и справа называются односторонними приделами. Если существует лимит 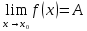 , то существуют два односторонних придела, при этом , то существуют два односторонних придела, при этом 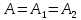 Функции 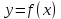 называется бесконечно малой при называется бесконечно малой при 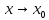 если если 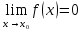 Алгебраическая сума конечного числа бесконечно малых функций есть бесконечно малая функция. Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция. Так как любая бесконечно малая функция ограничена, то произведение двух бесконечно малых функций есть бесконечно малая функция. Произведение бесконечно малой функции на число есть бесконечно малая функция. Частное от деления бесконечно малой функции от функции, имеющий отличный от нуля придел, есть бесконечно малая функция. Если функция 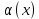 ― бесконечно малая ― бесконечно малая 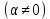 , то функция , то функция 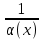 есть бесконечно большая функция и на оборот: если функция есть бесконечно большая функция и на оборот: если функция 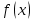 ― бесконечно большая, то ― бесконечно большая, то 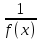 ― бесконечно малая. ― бесконечно малая.Если функция имеет придел, равный числу А, то её можно представить как суму числа А и бесконечно малой функции, т.е. 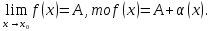 Если функцию можно представить в виде сумы числа А и бесконечно малой функции, то число А является её приделом, т.е. если 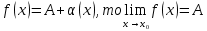 Придел сумы (разности) двух функций равен сумме (разности) их приделов 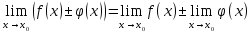 Функция может иметь только один предел при 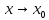 . .Предел произведения двух функций равен произведения их приделов 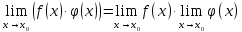 Постоянный множитель можно выносить за знак придела 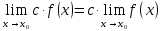 Предел степени с натуральным показателем равен той же степени придела 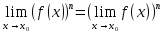 Придел дроби равен приделу числителя делённого на придел знаменателя, если придел знаменателя не равен нулю 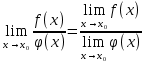 Первый замечательный придел это придел отношения синуса к его аргументу равному единице, когда аргумент стремится к нулю 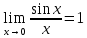 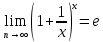  Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Точки разрыва делятся на два вида: на точки разрыва первого рода и на точки разрыва второго рода. Точки разрыва первого рода это точки в которых существуют конечные односторонние приделы функции, а точки второго рода это точки в которых не существует один односторонний придел функции или он бесконечен.  Если D =0 , то оно принимает вид 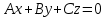 Если С=0 , то оно имеет вид 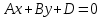 Если С=D=0, то оно проходит через О(0;0;0) Если A=B=0, то оно имеет вид Cz+D=0 Если A=B=D, то оно имеет вид 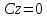   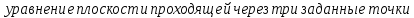 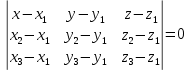 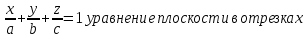 Функция называется не прерывной в точке, если существует придел функции в этой точке и он равен значению функции в этой точке т.е. 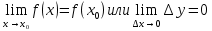 Равенство означает выполнение трёх условий Функция 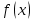 определена в точке определена в точке 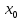 и в её окрестности и в её окрестностиФункция 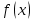 имеет придел имеет придел 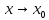 Придел функции в точке 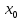 равен значению функции в этой точке равен значению функции в этой точкеФункция 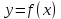 называется непрерывной на отрезке [a;b], если она не прерывна на в интервале (a;b) и в точке x=a непрерывна справа, а в точке x=b непрерывна слева. называется непрерывной на отрезке [a;b], если она не прерывна на в интервале (a;b) и в точке x=a непрерывна справа, а в точке x=b непрерывна слева.Производной функции 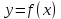 называется придел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю называется придел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю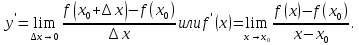 Если функция описывает физический процесс и её производная является скоростью протекания этого процесса ― физический смысл производной. Если функция описывает физический процесс и её производная является скоростью протекания этого процесса ― физический смысл производной.Производная в точке х равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна х. ― геометрический смысл производной. Дифференциалом функции 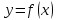 в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, и обозначается 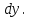 Этот дифференциал называют дифференциалом первого порядка Этот дифференциал называют дифференциалом первого порядка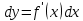 Дифференциал функции равен произведению этой функции на дифференциал независимой переменной. 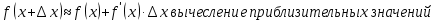 Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. 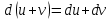 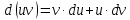 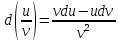 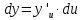 Если функция 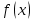 непрерывна на отрезке [a;b], дифференцируемая на интервале (a;b) и на концах отрезка принимает одинаковые значения непрерывна на отрезке [a;b], дифференцируемая на интервале (a;b) и на концах отрезка принимает одинаковые значения 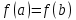 , то найдётся хоть бы одна точка , то найдётся хоть бы одна точка 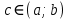 , в которой производная , в которой производная 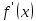 обращается в нуль, т.е. обращается в нуль, т.е. 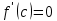 Если функция 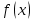 непрерывна на отрезке [a;b], дифференцируемая на интервале (a;b), то найдётся хотя бы одна точка непрерывна на отрезке [a;b], дифференцируемая на интервале (a;b), то найдётся хотя бы одна точка 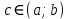 такая, что выполняется равенство такая, что выполняется равенство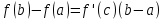 Пусть функции 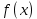 и и 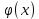 непрерывны и дифференцируемые в окрестности точки непрерывны и дифференцируемые в окрестности точки 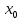 и обращаются в нуль в этой точке: и обращаются в нуль в этой точке: 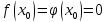 . Если существует придел . Если существует придел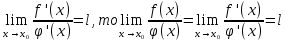 Пусть функции 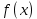 и и 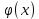 непрерывны и дифференцируемые в окрестности точки непрерывны и дифференцируемые в окрестности точки 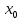 (кроме точки (кроме точки 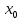 ), в этой окрестности ), в этой окрестности 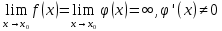 . Если существует придел . Если существует придел 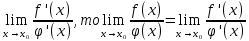 . .Придел 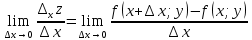 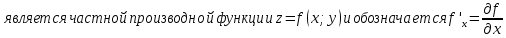 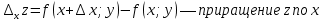 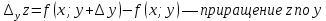 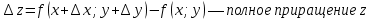 Главная часть приращения функции 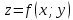 называется полным дифференциалом этой функции и обозначается символом называется полным дифференциалом этой функции и обозначается символом 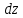 . . Если функция дифференцируема в точке, то она не прерывна в этой точке и имеет в ней частные производные 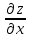 и и  причём причём 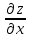 = A, = A,  = B. = B. Если функция имеет непрерывные частные производные, то она дифференцируема в этой точке и её полный дифференциал выражается формулой 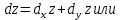 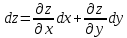 Точка называется точкой максимума функции, если существует окрестность точки 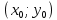 , что для каждой точки (a;b), отличной от , что для каждой точки (a;b), отличной от 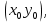 из этой окрестности выполняется неравенство из этой окрестности выполняется неравенство 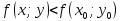 , а для минимума , а для минимума 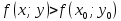 Если в точке дифференцируемая функция имеет экстремум, то её частные производные в этой точке равны нулю: 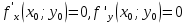 Пусть в стационарной точке и некоторой её окрестности функция имеет непрерывные частные производные до второго порядка включительно, тогда Если 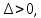 то функция в точке имеет экстремум: минимум A > 0, максимум A < 0 то функция в точке имеет экстремум: минимум A > 0, максимум A < 0Если 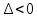 , то функция в точке не имеет экстремум , то функция в точке не имеет экстремум   |
