Навигация по странице:(j,j)(i,j)( i=1, j=8 ), ( i=2, j=8 ), (i=1, j=7),( i=5, j=5 ), (i=8, j=6)Случая 1 и Случая 2 :var a, b: real; begin readln(a, b); if b > 0 then if a > 0 then
|
Ответы на задачи 24 (С1)
var x0, y0: real;
begin
readln (x0, y0)
if (x0 < 2) and (x0 > -2) and
(y0 < 2) and (y0 > -2) then
writeln('точка лежит внутри области')
else writeln('точка не лежит внутри области');
end.
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
2
|

|
|
|
|
|
|
|

|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| Легко проверить, что клетка (i=5,j=4) удовлетворяет условию i=9-j, и, следовательно, сложному условию (i=9-j) OR (i=j) (OR означает логическую операцию «ИЛИ» - выполнение хотя бы одного из двух условий)
Для ответа на остальные вопросы нарисуем поле и расставим королей (в самом деле в этой задаче все равно, какого цвета поля, поэтому мы их не раскрашивали).
Короли могут ходить по диагонали, поэтому чтобы дойти до поля (i,j), королю лучше
сначала идти по диагонали, чтобы быстрее выйти на нужную горизонталь или вертикаль, а затем двигаться по этой горизонтали (или вертикали) к заданной клетке.
черный король [его координаты (1,1)] идет по диагонали k-1 шагов, где k=min(i,j) до клетки с координатами (i,i) (если i<=j) или до клетки (j,j) (если i>=j); затем он делает оставшееся количество шагов, max(i,j)-k, по горизонтали или вертикали, так что его общее число шагов равно
max(i,j)-1
аналогично белый король [его координаты (8,1)] идет по диагонали q-1 шагов, где q=min(9-i,j) до клетки с координатами (9-i,9-i) (если 9-i<=j) или до клетки (j,j) (если 9-i>=j); затем он делает оставшееся количество шагов, max(9-i,j)-q, по горизонтали или вертикали, так что его общее число шагов равно
max(9-i,j)-1
таким образом, нас интересуют клетки (i,j), для которых
max(i,j)-1= max(9-i,j)-1 или max(i,j)= max(9-i,j) (*)
(1,8)
|
(2,8)
|
|
|
|
|
|
|
8
|
(1,7)
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
(8,6)
|
6
|
|
|
|
|
(5,5)
|
|
|
|
5
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
2
|

|
|
|
|
|
|
|

|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| Чтобы найти все пары (i,j), для которых верно полученное равенство, рассмотрим сначала левую половину доски (i<=4):
если i<=4, то 9-i>=5>i, поэтому равенство (*) справедливо только при j>=9-i; это область выше главной диагонали и на ней;
в силу симметрии сразу можно построить соответствующую область и в правой части доски (см. рисунок справа):
Из указанных полей только три, выделенные желтым маркером, оказываются внутри нужной области
(i=1, j=8), (i=2, j=8), (i=1, j=7),
(i=5, j=5), (i=8, j=6)
Правильное условие, определяющее нужную область, выглядит так: «клетка выше главной диагонали (или на ней) и одновременно выше второй диагонали (или на ней)». Остается записать его на Паскале:
(j>=i) and (j>=9-i)
Доработка программы сводится просто к замене условия, все остальное правильно.
Попробуем прежде всего найти математическое решение неравенства 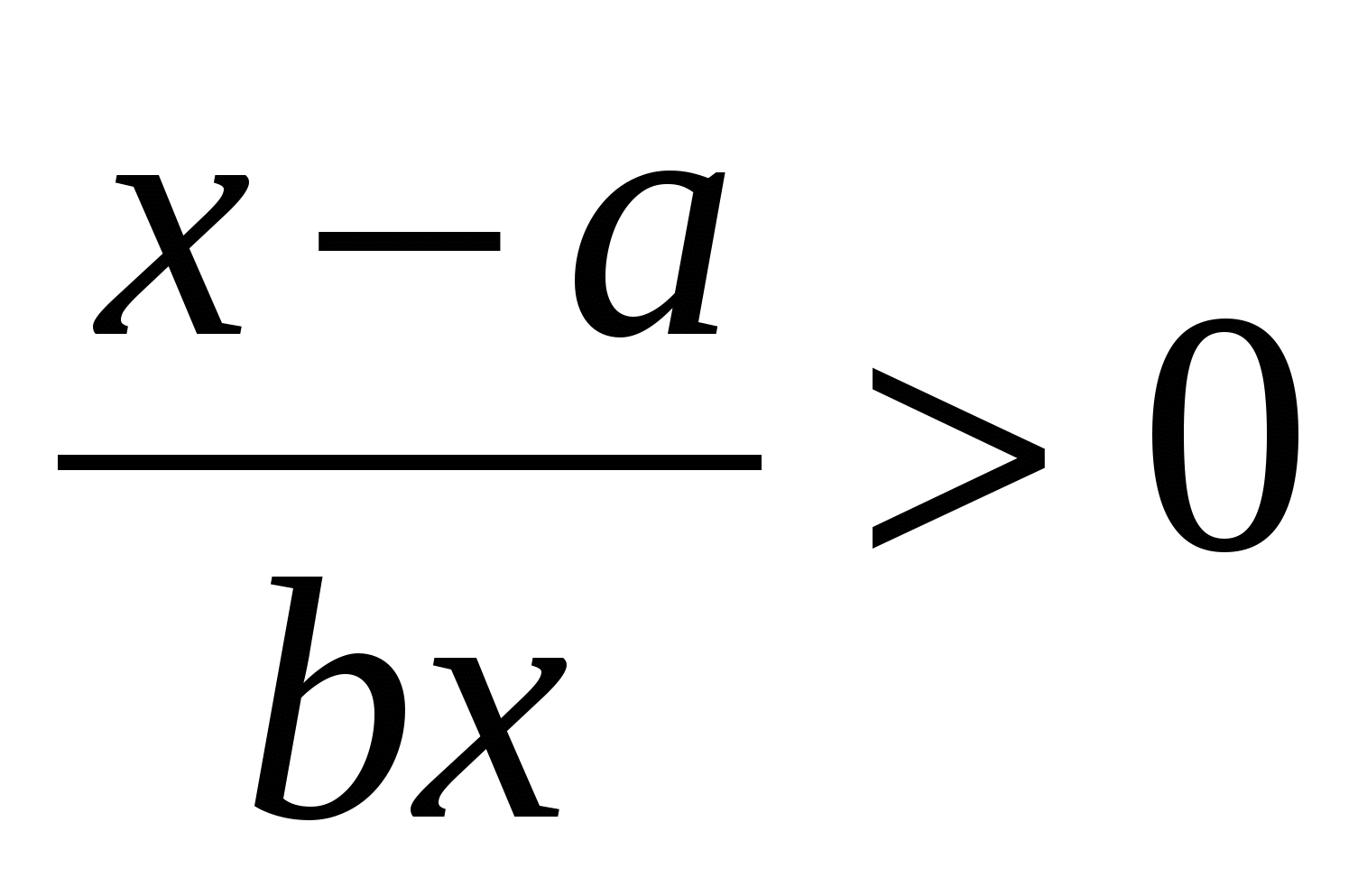 . Оно истинно, если числитель и знаменатель дроби имеют один знак, или оба положительные, или оба отрицательные. При . Оно истинно, если числитель и знаменатель дроби имеют один знак, или оба положительные, или оба отрицательные. При 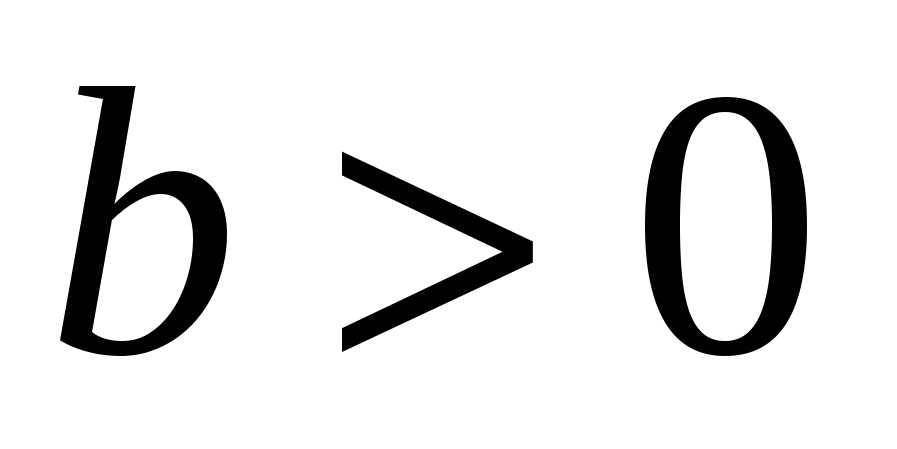 получаем: получаем:
(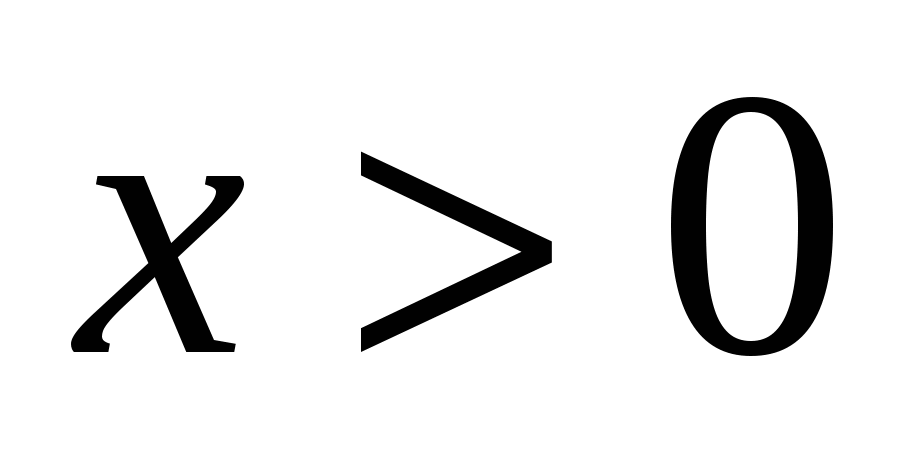 и и 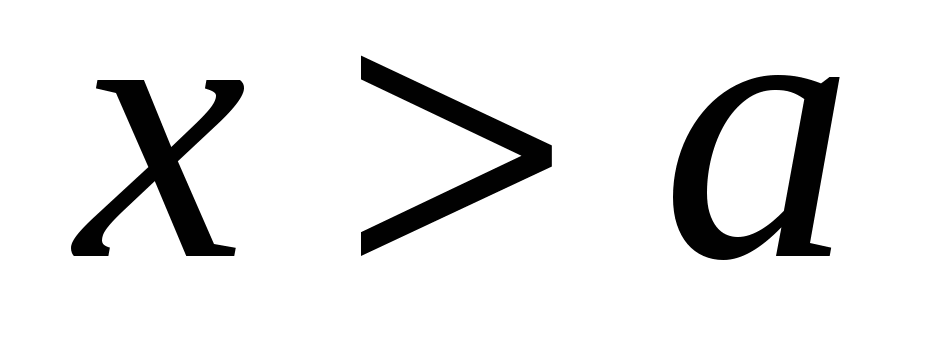 ) или ( ) или (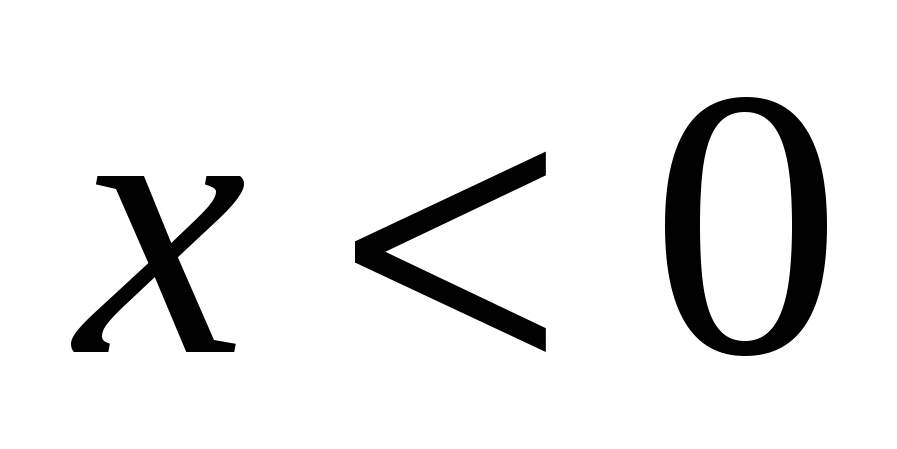 и и 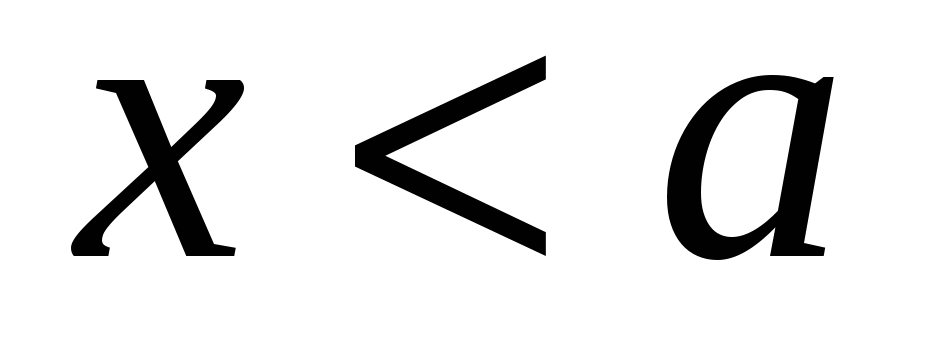 ) )
В краткой форме: 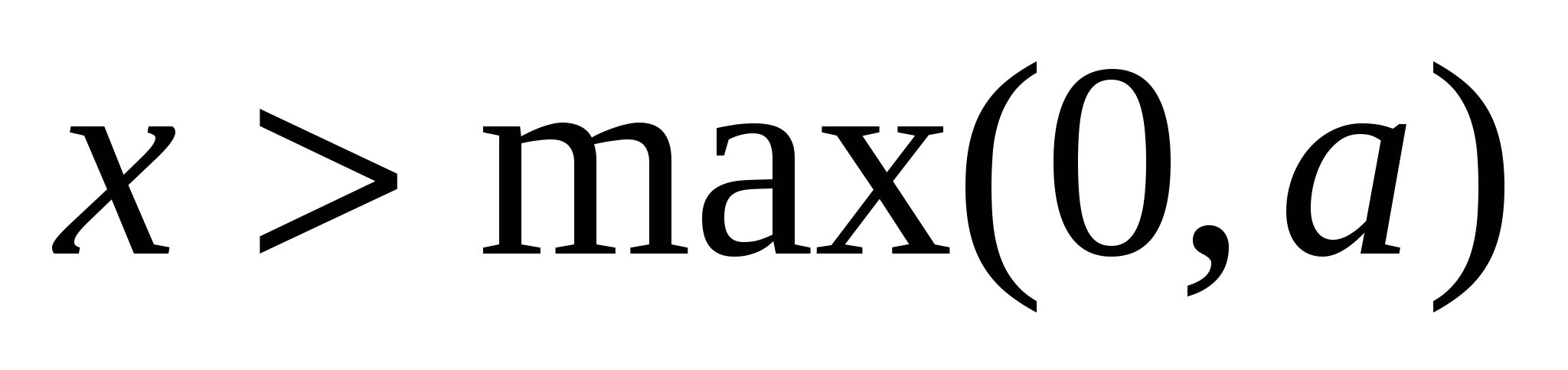 или или  . В зависимости от значения . В зависимости от значения  получаем получаем
Случай 1. При 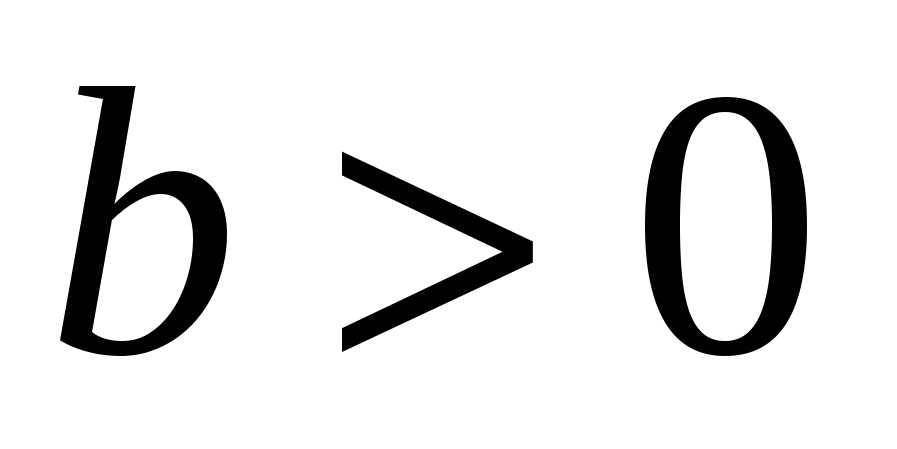 и и 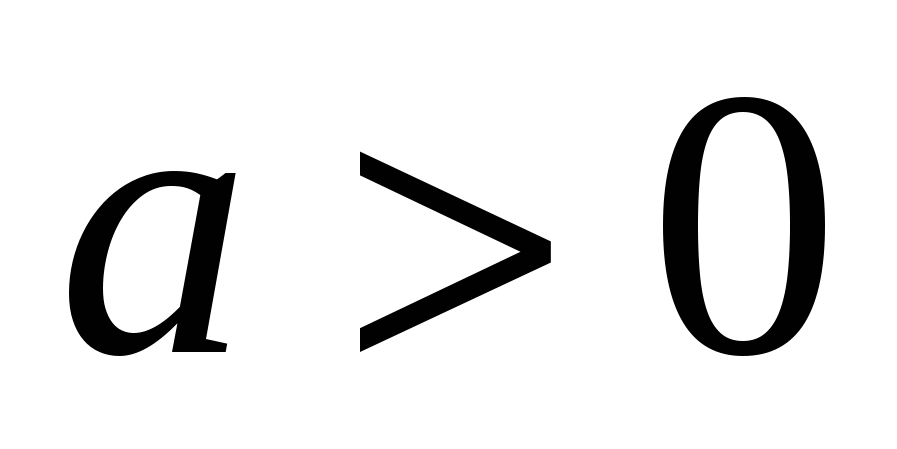 : : 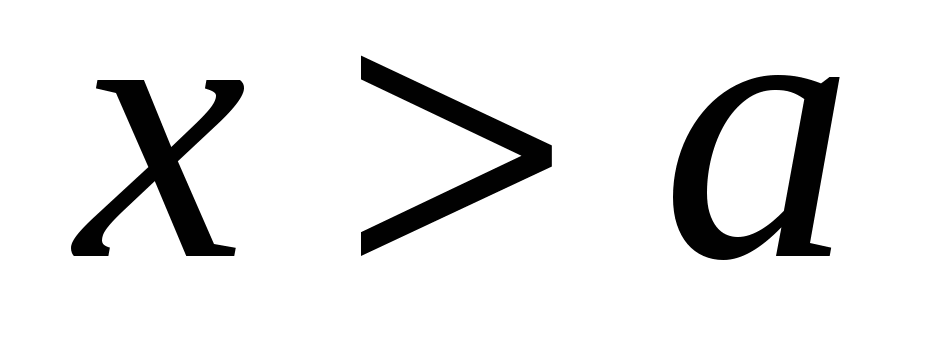 или или 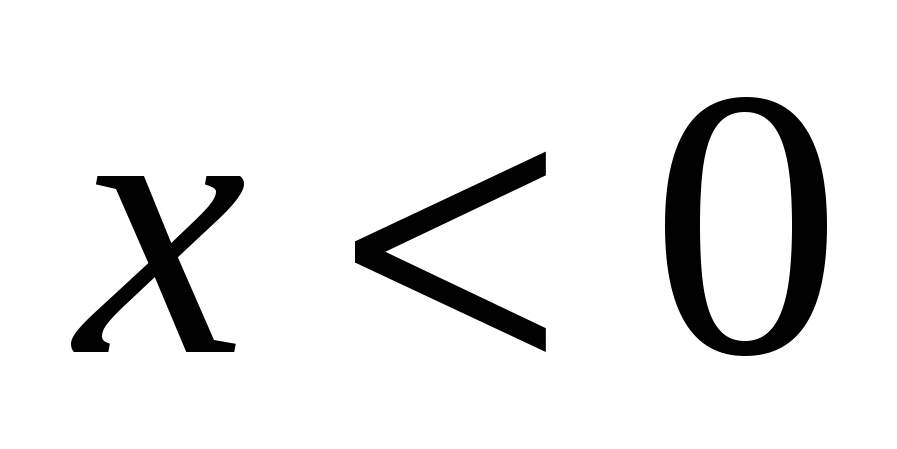
Случай 2. При 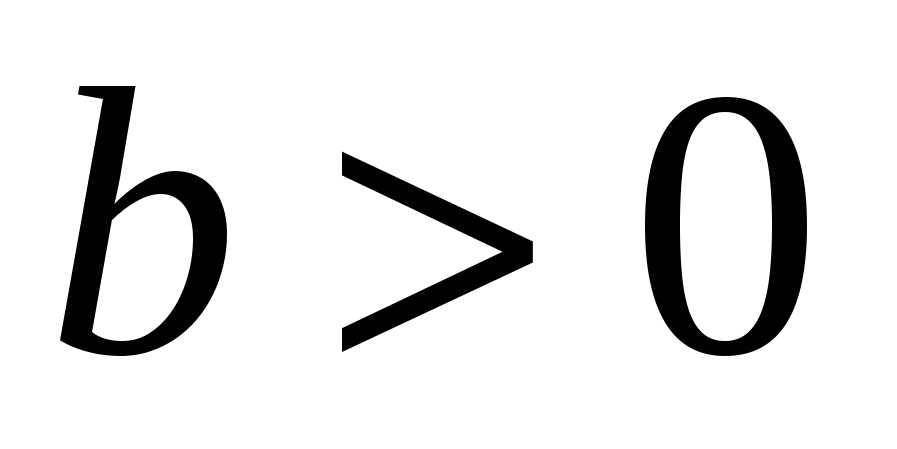 и и 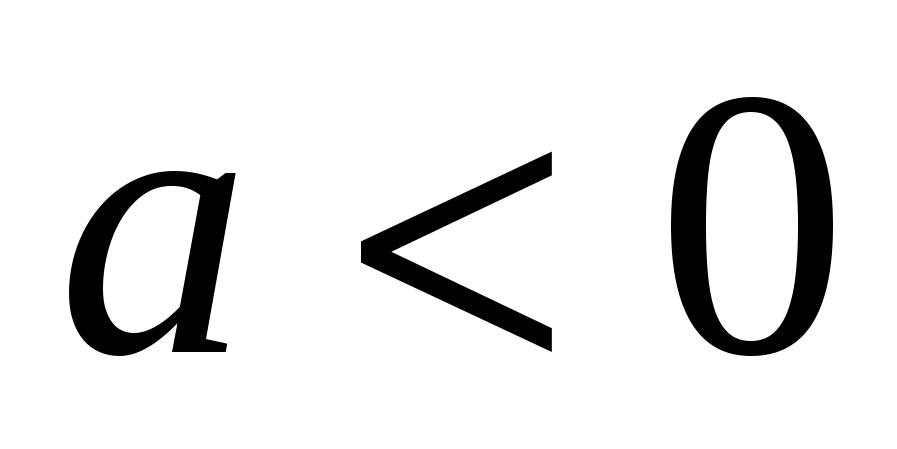 : : 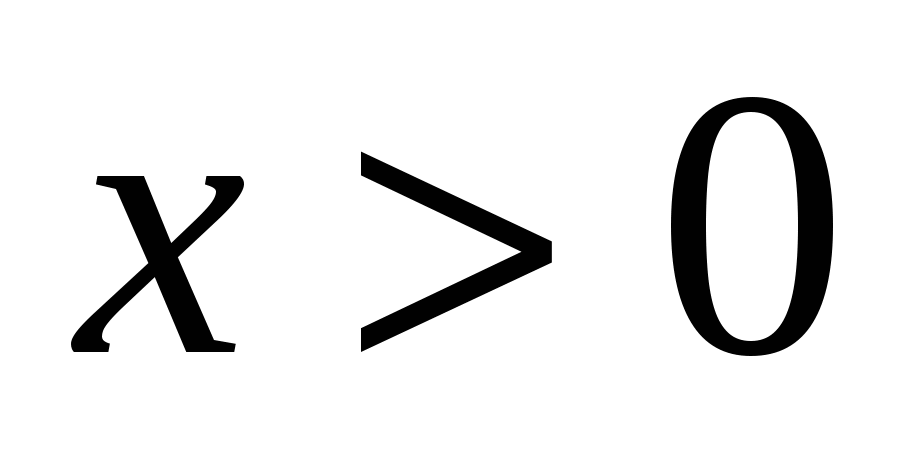 или или 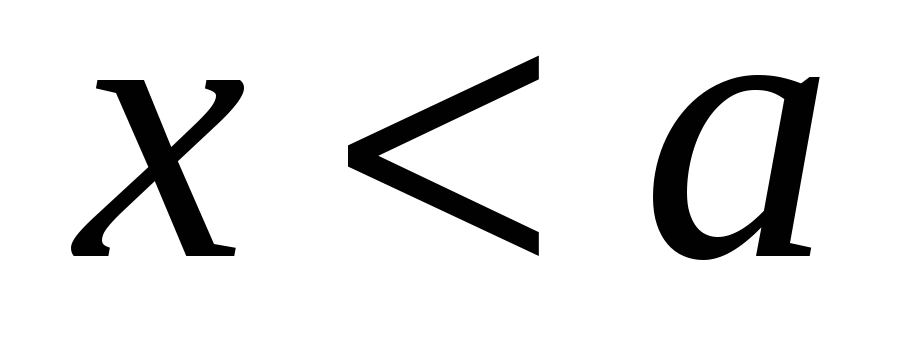
Теперь рассмотрим случай 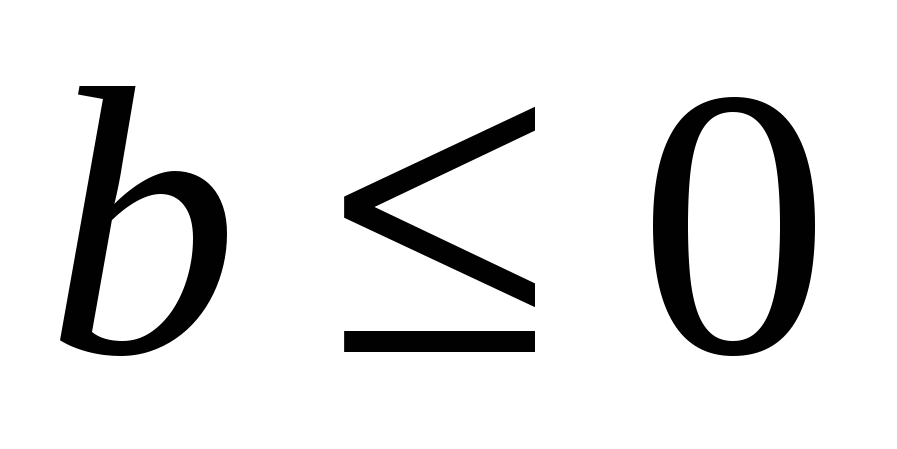 . Снова получаем два варианта: . Снова получаем два варианта:
(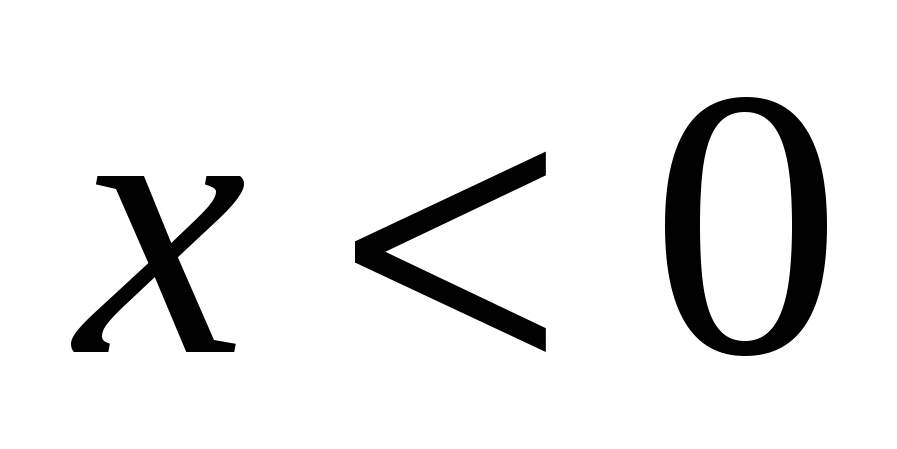 и и 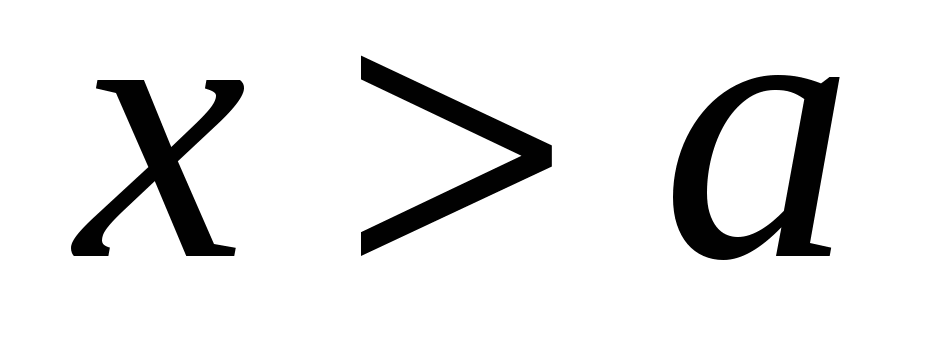 ) или ( ) или (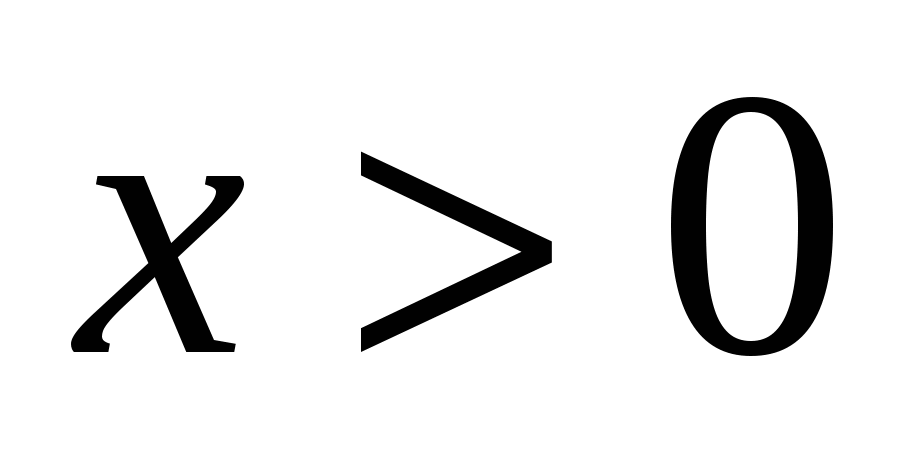 и и 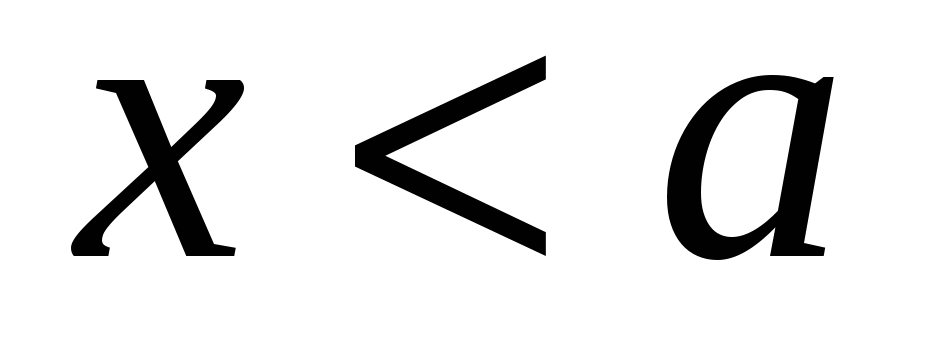 ) )
При 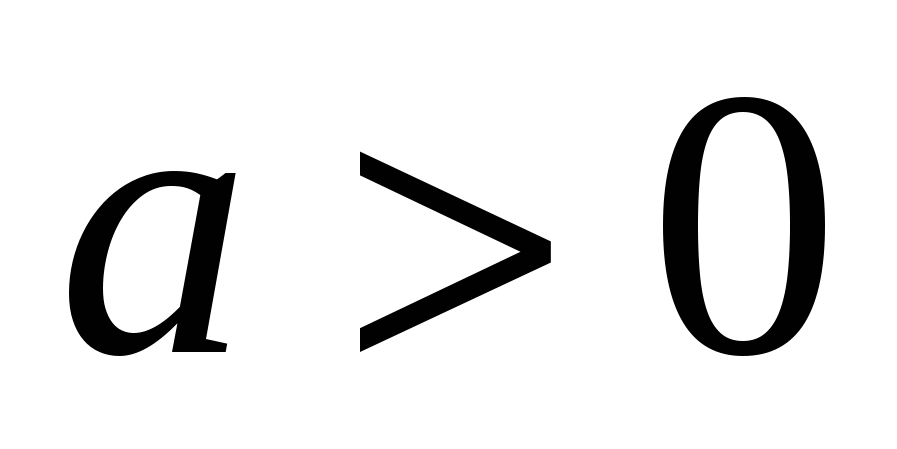 всегда ложно выражение в первых скобках, а при всегда ложно выражение в первых скобках, а при 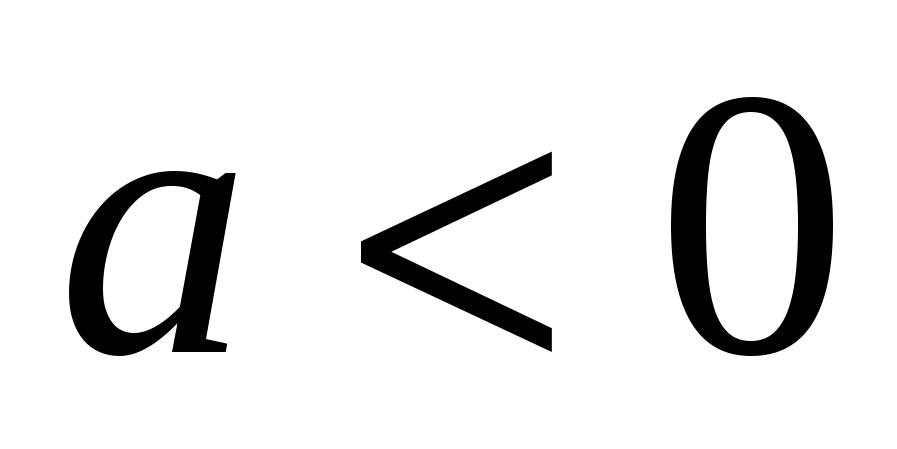 – выражение во вторых скобках. Поэтому можно записать еще два случая через двойные неравенства: – выражение во вторых скобках. Поэтому можно записать еще два случая через двойные неравенства:
Случай 3. При 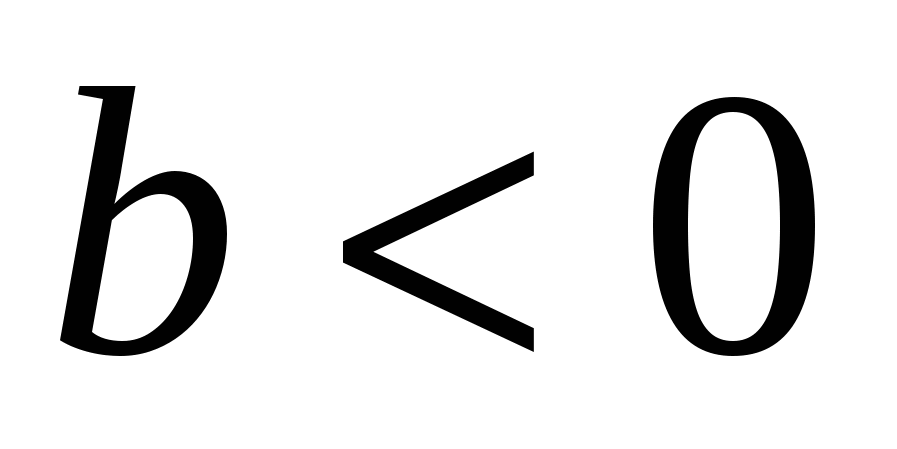 и и 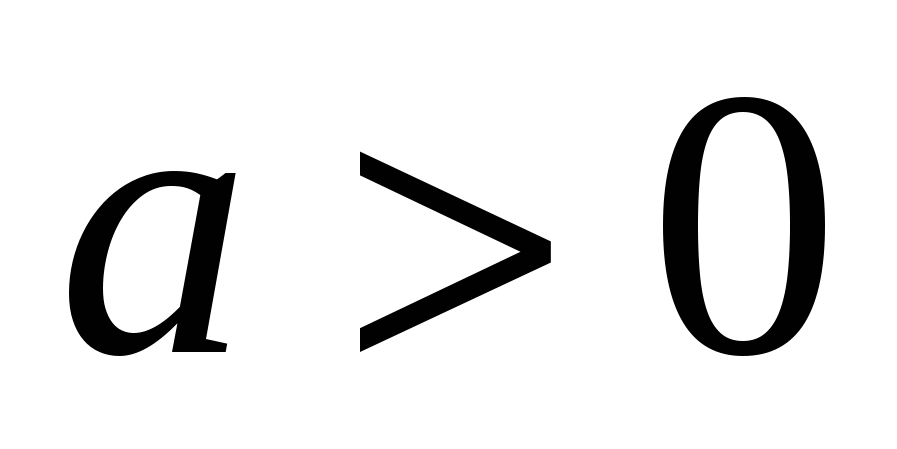 : : 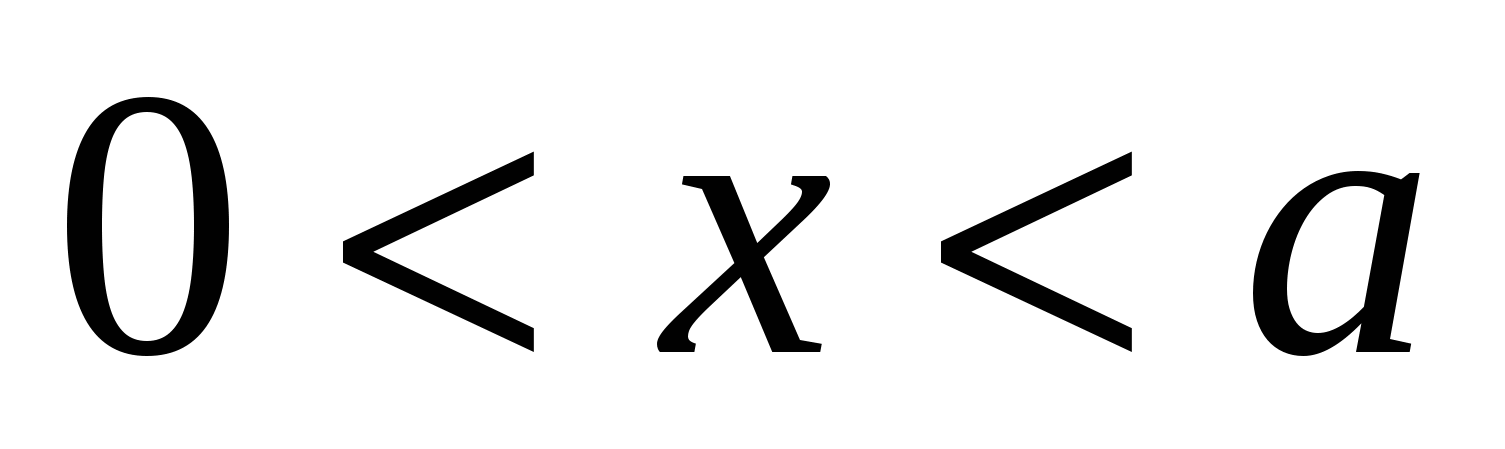
Случай 4. При 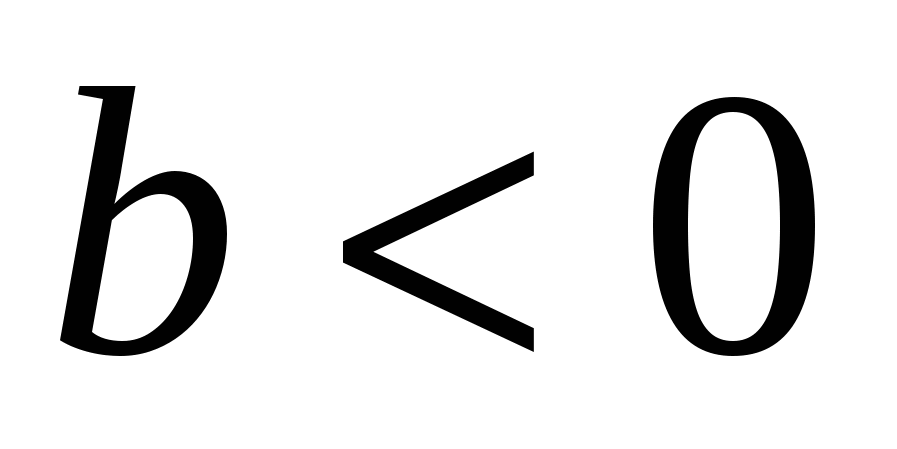 и и 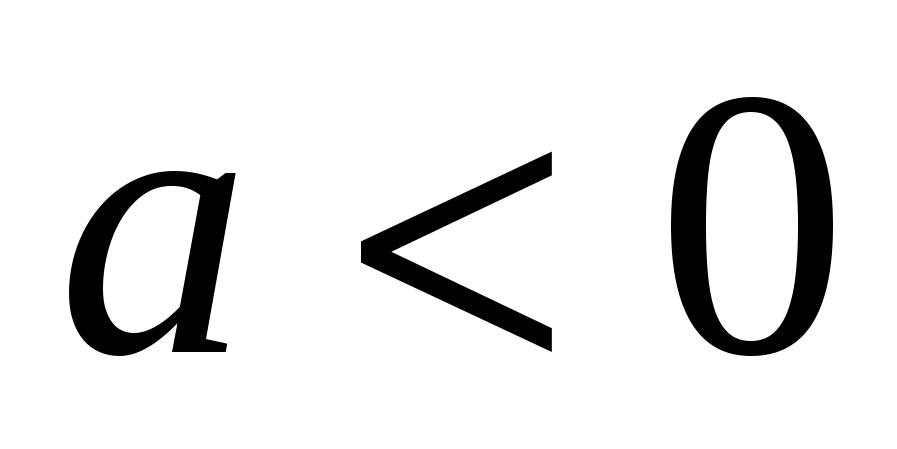 : : 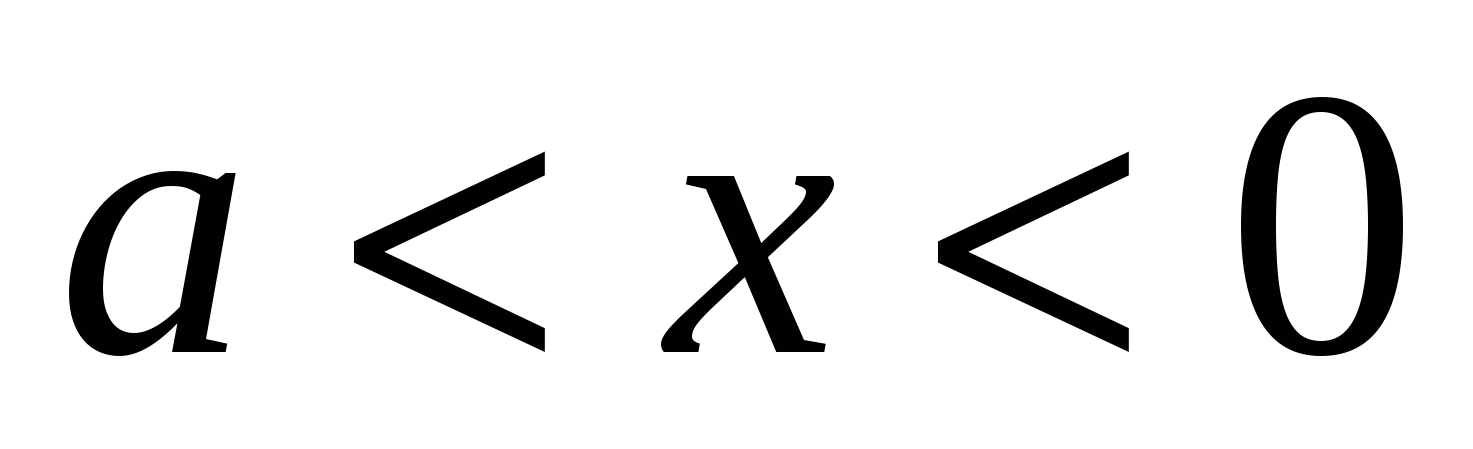
Запишем основную часть программы, определив принадлежность каждого else-блока и используя запись «лесенкой»:
if b > 0 then
write('x > ', a, ' или x < 0')
else
if a > 0 then
write('0 < x < ', a)
else
write(a, ' < x < 0');
Анализ условных операторов показывает, что неправильно обрабатывается Случай 2 (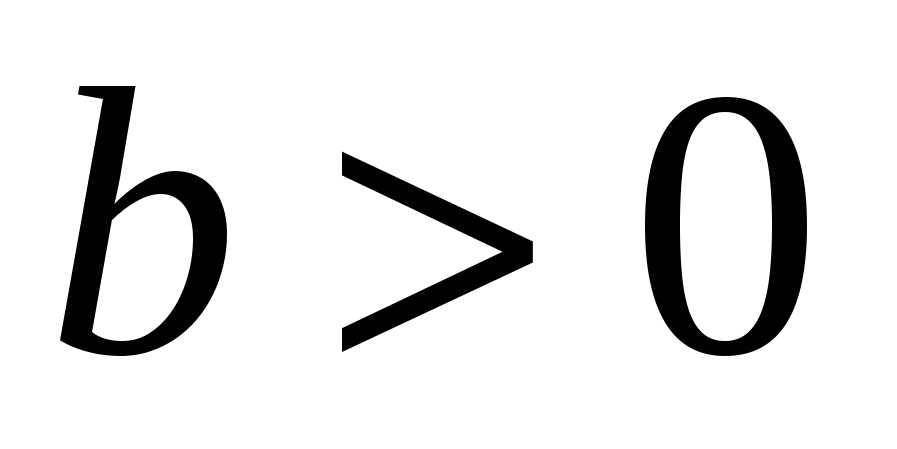 и и 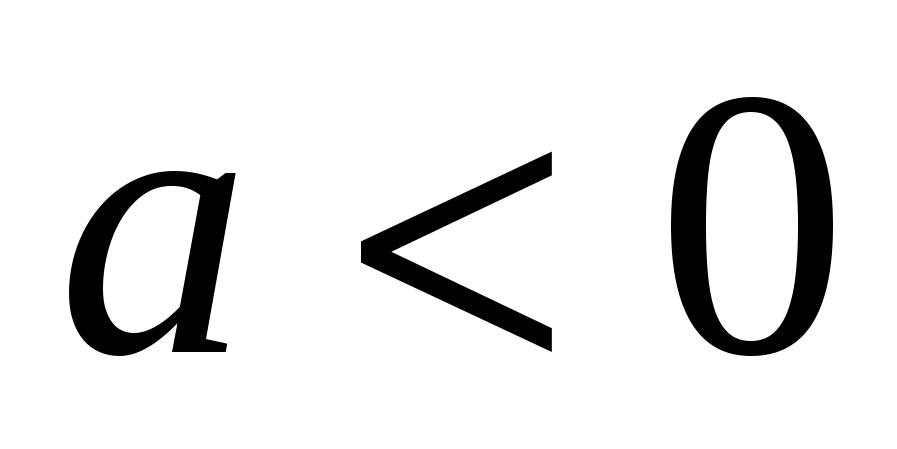 ), то есть, в качестве примера можно привести пару ), то есть, в качестве примера можно привести пару 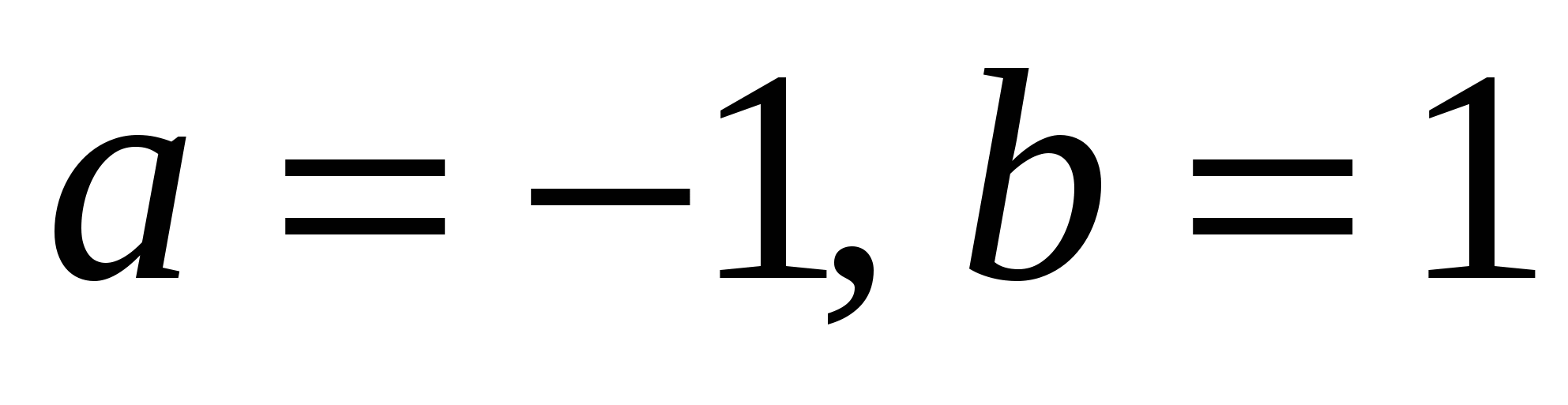 при любом при любом 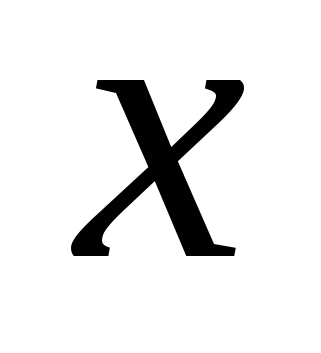 (которое вообще не влияет на результат). (которое вообще не влияет на результат).
В программе вводится переменная 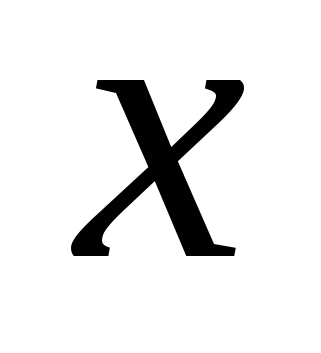 , которая нигде не используется. Поэтому это – лишняя часть программы, можно убрать , которая нигде не используется. Поэтому это – лишняя часть программы, можно убрать 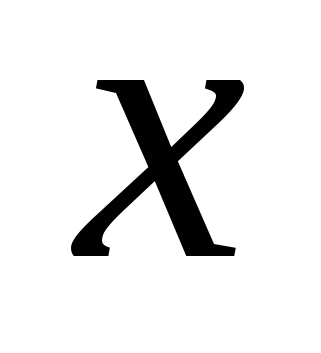 из списка объявляемых переменных и списка ввода в операторе readln. из списка объявляемых переменных и списка ввода в операторе readln.
Простейший и (в данной задаче) наиболее логичный вариант доработки программы – добавить еще один условный оператор для правильного разделения Случая 1 и Случая 2:
var a, b: real;
begin
readln(a, b);
if b > 0 then
if a > 0 then
write('x > ', a, ' или x < 0')
else
write('x < ', a, ' или x > 0')
else
if a > 0 then
write('0 < x < ', a)
else
write(a, ' < x < 0');
end.
П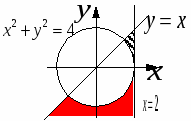 ервое условие в программе, x*x+y*y >= 4, означает «вне круга». Если выполняются одновременно второе и третье условия, x <= 2 и y <= x, точка находится в секторе между прямыми ервое условие в программе, x*x+y*y >= 4, означает «вне круга». Если выполняются одновременно второе и третье условия, x <= 2 и y <= x, точка находится в секторе между прямыми 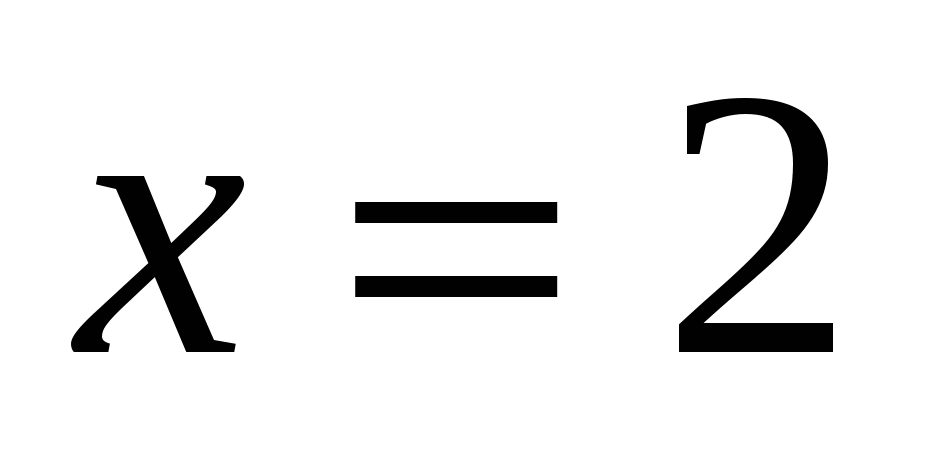 и и 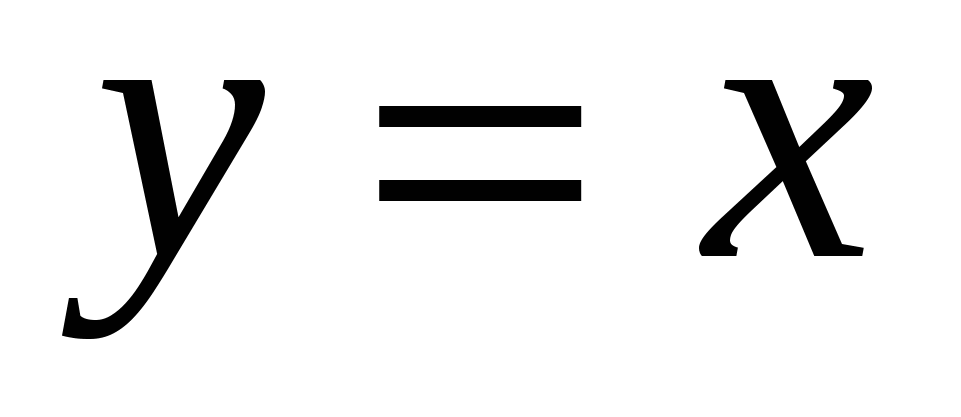 , в который входит заштрихованная область. Таким образом, выполнение всех трех условия означает «вне круга и в секторе». Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Поэтому для любой точки в «красной зоне», например, для точки (1; –2), программа выдаст неправильный ответ «принадлежит». , в который входит заштрихованная область. Таким образом, выполнение всех трех условия означает «вне круга и в секторе». Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Поэтому для любой точки в «красной зоне», например, для точки (1; –2), программа выдаст неправильный ответ «принадлежит».
Если записать программу «лесенкой», становится видна еще одна ошибка.
if x*x+y*y >= 4 then
if x <= 2 then
 if y <= x then if y <= x then
write('принадлежит')
else
write('не принадлежит')
Дело в том, что любой else относится к ближайшему if, поэтому сообщение «не принадлежит» выводится только тогда, когда первые два условия выполняются, а третье – нет. Следовательно, для точки (0;0), например, программа вообще не выдаст никакого сообщения (первое условие ложно).
Чтобы исправить программу, можно добавить еще одно условие y >= 0 (это отсекает «красную зону») и объединить все четыре условия в одно сложное условие:
var x,y: real;
begin
readln(x,y);
if (x*x+y*y >= 4) and (x <= 2) and
(y <= x) and (y >= 0) then
write('принадлежит')
else
write('не принадлежит')
end.
З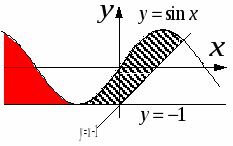 аписанные в программе условия означают «ниже синусоиды» и в секторе между прямыми аписанные в программе условия означают «ниже синусоиды» и в секторе между прямыми 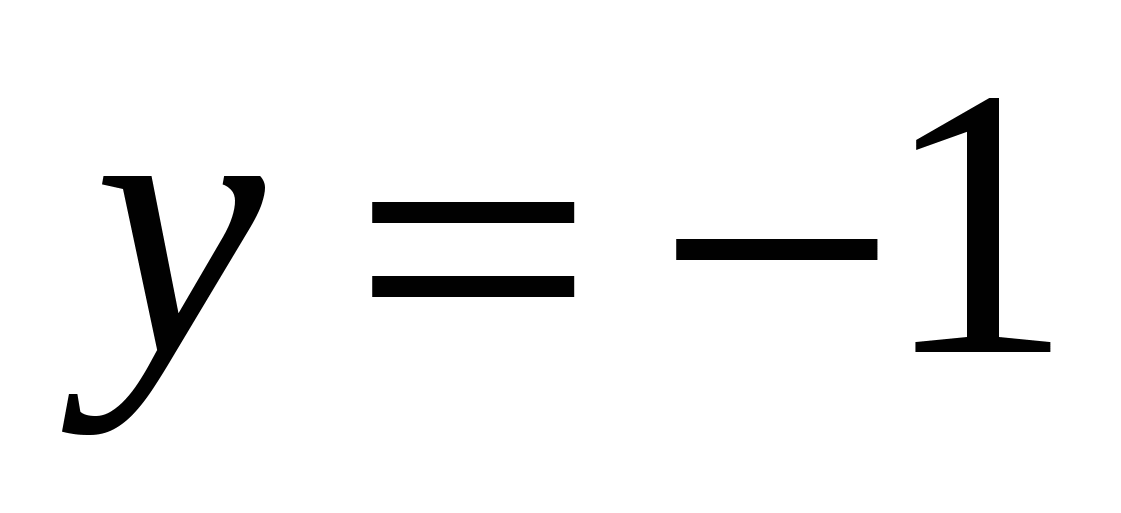 и и 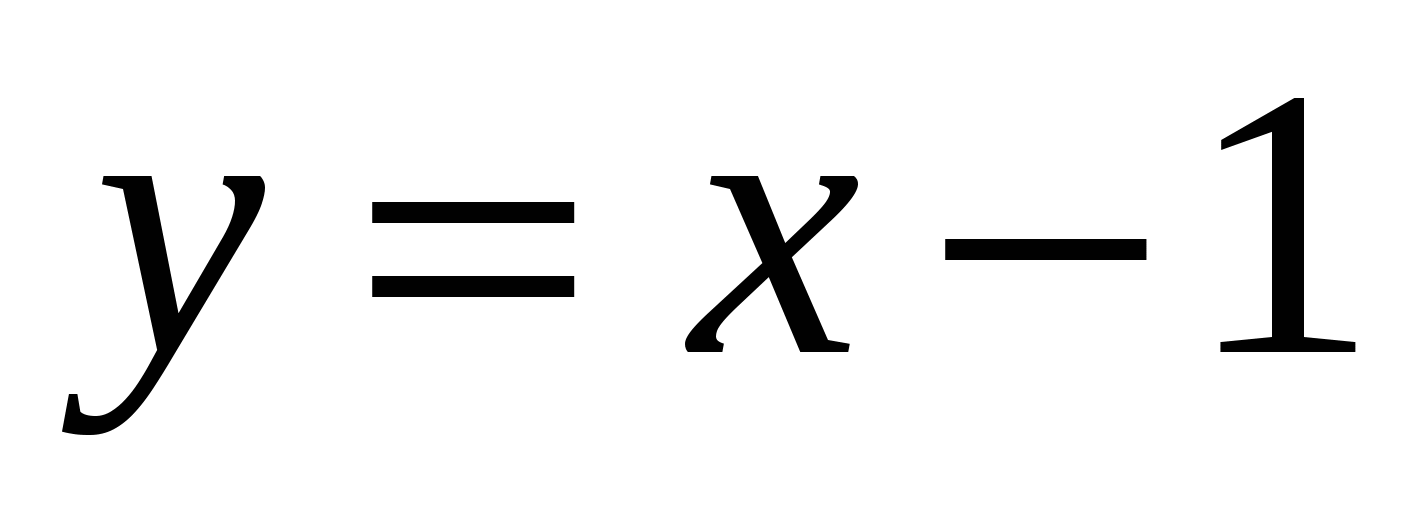 , в который входит заштрихованная область. Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Первое пересечение синусоиды с осью абсцисс происходит при , в который входит заштрихованная область. Однако, этому условию удовлетворяет не только заштрихованная область, но еще и вся бесконечная область, выделенная на рисунке красным цветом. Первое пересечение синусоиды с осью абсцисс происходит при 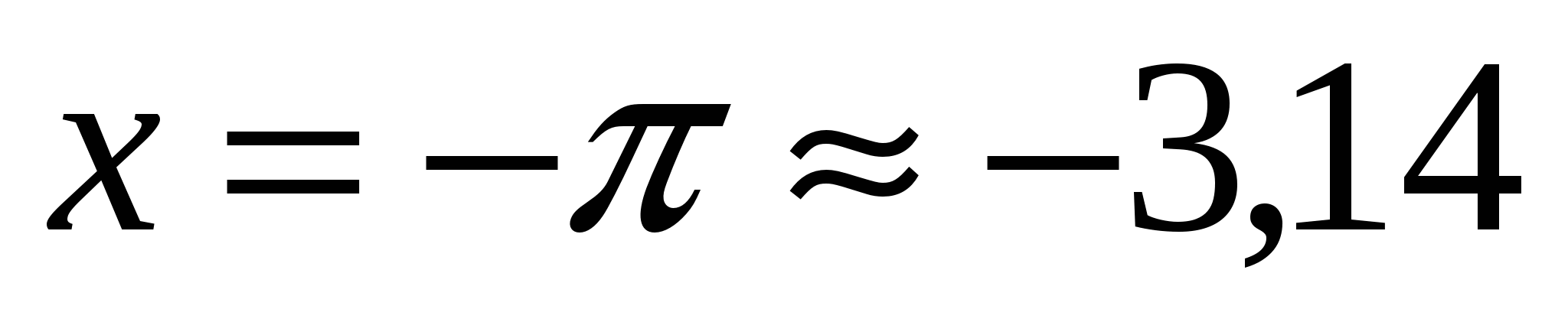 , поэтому программа выдает неверный ответ «принадлежит», например, для точки (-4;0), которая в самом деле не принадлежит заштрихованной области. , поэтому программа выдает неверный ответ «принадлежит», например, для точки (-4;0), которая в самом деле не принадлежит заштрихованной области.
Если записать программу «лесенкой», становится видна еще одна ошибка.
|
|
|
 Скачать 1.99 Mb.
Скачать 1.99 Mb. if y <= x then
if y <= x then 
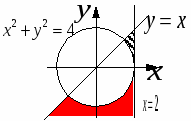 ервое условие в программе, x*x+y*y >= 4, означает «вне круга». Если выполняются одновременно второе и третье условия, x <= 2 и y <= x, точка находится в секторе между прямыми
ервое условие в программе, x*x+y*y >= 4, означает «вне круга». Если выполняются одновременно второе и третье условия, x <= 2 и y <= x, точка находится в секторе между прямыми 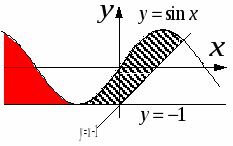 аписанные в программе условия означают «ниже синусоиды» и в секторе между прямыми
аписанные в программе условия означают «ниже синусоиды» и в секторе между прямыми