Ответынавопросы
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Что такое кинетическая энергия материальной точки? С работой какой силы она связана и как? Ответ: Пусть вдоль оси x движется частица массой m. Пусть на частицу действует постоянная сила F, параллельная оси x. Динамическое уравнение, спроецированное на ось x, будет иметь вид: 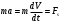 . Умножим обе части этого уравнения на скорость частицы V и перенесём величину dt в правую часть: . Умножим обе части этого уравнения на скорость частицы V и перенесём величину dt в правую часть: 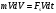 . Учитывая, что . Учитывая, что 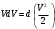 и и 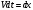 , где dx – элементарное приращение частицы за время dt, получаем , где dx – элементарное приращение частицы за время dt, получаем 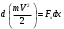 . Величина . Величина 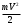 называется кинетической энергией, а называется кинетической энергией, а 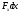 - элементарной работой. - элементарной работой. Какие силы называют консервативными? Приведите примеры таких сил. Ответ: Работа силы по перемещению частицы из одной точки в другую в общем случае зависит от формы траектории между этими точками. Существуют силы, работа которых не зависит от формы траектории, а определяется только положением начальной и конечной точки. Такие силы называются консервативными. Определение: сила является консервативной, если её работа на замкнутой траектории равна нулю 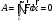 . . Примеры: сила тяжести, сила упругости – консервативные силы. Консервативными являются все силы, которые обратно пропорциональны квадрату расстояния между взаимодействующими телами. Что такое потенциальная энергия материальной точки? С работой какой силы она связана и как? Ответ: Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. В то время, как кинетическая энергия всегда характеризует тело относительно выбранной системы отсчёта, потенциальная энергия всегда характеризует тело относительно источника силы (силового поля). Потенциальная энергия связана с силой тяжести. Рассмотрим тело, находящееся на высоте h над землёй. Если тело закреплено, то сила тяжести не совершает работу. Но сила тяжести потенциально способна совершить работу: если тело освободить, оно начнёт перемещаться и сила тяжести будет совершать работу. Что такое полная механическая энергия материальной точки? С работой какой силы она связана и как? Ответ: Пусть некоторая частица находится в стационарном поле консервативных сил. Со стороны этого поля на частицу действует консервативная сила Fконс. Работа, совершаемая этой силой, с одной стороны, идёт на приращение кинетической энергии частицы, движущейся под действием силы Fконс, а с другой – равна убыли потенциальной энергии этой частицы. Но это значит, что приращение кинетической энергии частицы равно убили её потенциальной энергии 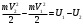 . Перегруппировав члены этого уравнения, получаем . Перегруппировав члены этого уравнения, получаем 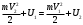 . Из этого следует, что сумма кинетической и потенциальной энергии частицы, движущейся в стационарном консервативном поле, остаётся постоянной. Величину . Из этого следует, что сумма кинетической и потенциальной энергии частицы, движущейся в стационарном консервативном поле, остаётся постоянной. Величину 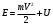 называют полной механической энергией частицы. называют полной механической энергией частицы.Сформулируйте закон сохранения механический энергии для материальной точи. Ответ: Полная механическая энергия частицы может измениться под действием только сторонних сил. Отсюда вытекает закон сохранения механической энергии частицы: если сторонние силы отсутствуют или не совершают работы, то полная механическая энергия частицы в стационарном поле потенциальных сил остается постоянной. Что такое полная механическая энергия системы материальных точек. С работой какой силы она связана и как? Ответ: Пусть имеется система из двух взаимодействующих тел. Предположим, что силы, возникающие при взаимодействии этих тел, консервативны. Если под действием внутренних сил одно из тел изменит своё положение относительно другого, то работа внутренней силы будет равна убыли его потенциальной энергии. Потенциальная энергия этого тела обусловлена его взаимодействием с другим телом, принадлежащим этой системе. Поэтому её называют потенциальной энергией взаимодействия тел системы, или потенциальной энергией системы тел. Сформулируйте закон сохранения механической энергии для системы материальных точек. Ответ: Какой вид взаимодействия тел называют абсолютно упругим ударом? Приведите примеры. Ответ: Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии и закон сохранения импульса. 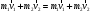 Какой вид взаимодействия тел называют абсолютно неупругим ударом? Приведите примеры. Ответ: Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу. 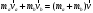 Какие силы называют диссипативными? Приведите примеры. Ответ: Диссипативные силы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту. Пример: сила трения скольжения. Ответы на вопросы для защиты лабораторных работ №2,3 по физике :3 Дайте определение понятия «вращательное движение». Ответ: Вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Дайте определение угловой координаты. Ответ: Угловая координата – полярный угол, на который можно повернуть против часовой стрелки полярную ось, для того чтобы попасть в точку, для которой определена данная угловая координата. 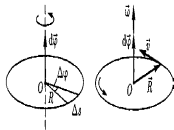 Дайте определение вектора углового перемещения. Как определяется его направление? Дайте определение вектора углового перемещения. Как определяется его направление?Ответ: Рассмотрим твёрдое тело, которое вращается вокруг неподвижной оси. Каждая точка этого тела описывает окружность равных промежутков. Бесконечно малые повороты 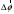 на некоторый угол можно рассматривать как векторы перемещения. на некоторый угол можно рассматривать как векторы перемещения. Модуль вектора 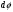 равен углу поворота, а направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта. равен углу поворота, а направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта. Д 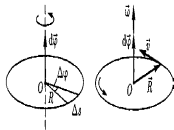 айте определение вектора угловой скорости. Как определяется его направление? айте определение вектора угловой скорости. Как определяется его направление?Ответ: Вектор угловой скорости – скользящий вектор, численно равный абсолютной величине угловой скорости и направленный вдоль оси вращения по правилу правого винта. 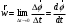 . Единица измерения угловой скорости – рад/сек. . Единица измерения угловой скорости – рад/сек.Дайте определение вектора углового ускорения. Как определяется его направление? Ответ: Вектор углового ускорения – производная по времени от вектора угловой скорости тела. 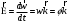 . Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. . Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.Дайте определение момента инерции (как рассчитывается и каков его физический смысл?) Ответ: Момент инерции - скалярная величина, характеризующая распределение масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат расстояний до базового множества (точки, прямой, поверхности). 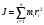 . В случае непрерывного распределения масс эта сумма сводится к интегралу . В случае непрерывного распределения масс эта сумма сводится к интегралу 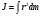 . .Момент инерции — величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси. Физический смысл: момент инерции является мерой инертности тела при вращении: 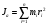 , где mi – масса i точки, ri – расстояние от точки i до оси. , где mi – масса i точки, ri – расстояние от точки i до оси.О 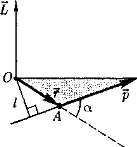 севой момент инертности тела Ja является мерой инертности тела во вращательном движении вокруг оси, подобно тому, как масса является мерой его инертности в поступательном движении. севой момент инертности тела Ja является мерой инертности тела во вращательном движении вокруг оси, подобно тому, как масса является мерой его инертности в поступательном движении. 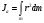 , где m – масса элемента тела. , где m – масса элемента тела.Дайте определение вектора момента импульса относительно точки, момента импульса относительно оси. Укажите направление вектора момент импульса. Ответ: Момент импульса относительно точки – векторная физическая величина, равная произведению радиус-вектора, проведённого от оси вращения к точке приложения импульса, на вектор этого импульса 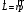 . . Момент импульса относительно неподвижной оси z – скалярная величина, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси. Дайте определение вектора момента силы относительно точки, момента силы относительно оси. Укажите направление вектора момент силы. Ответ: Момент силы относительно данной точки О - векторное произведение радиуса-вектора точки приложения силы, проведённого из точки О, на вектор силы 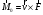 . .Момент силы направлен перпендикулярно плоскости, образованной точкой О и вектором силы, в ту сторону от этой плоскости, из которой силы F видна ориентированной против движения часовой стрелки. Момент силы относительно оси – момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. 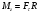 , где , где 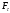 - проекция вектора силы на касательную к траектории вращения, а R – плечо силы (кратчайшее расстояние между осью вращения и линией действия силы, равное - проекция вектора силы на касательную к траектории вращения, а R – плечо силы (кратчайшее расстояние между осью вращения и линией действия силы, равное 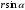 ). ).Назовите единицу измерения угловой скорости в системе СИ. Ответ: рад/сек Назовите единицу измерения углового ускорения в системе СИ. Ответ: рад/сек2 Назовите единицу измерения момента импульса в системе СИ. Ответ: кг*м2/сек Назовите единицу измерения момента силы в системе СИ. Ответ: Н*м Назовите единицу измерения момента инерции в системе СИ. Ответ: кг*м2 Как связаны линейные и угловые кинематические характеристики при вращательном движении? Ответ: Связь угловой и линейной скоростями. За время dt все точки тела повернутся на угол 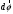 , перемещение при этом будет , перемещение при этом будет 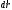 . Связь между перемещением и углом поворота: . Связь между перемещением и углом поворота: 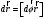 . Учитывая, что . Учитывая, что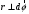 , то есть , то есть 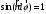 , получим выражение , получим выражение 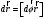 в скалярной форме: в скалярной форме: 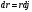 . По определению . По определению 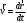 , подставив сюда , подставив сюда 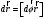 , получим , получим 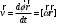 . Таким образом, получили связь между линейной и угловой скоростью . Таким образом, получили связь между линейной и угловой скоростью 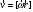 . .Связь между угловой и линейной ускорениями. По определению 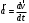 , подставив сюда , подставив сюда 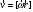 , получим , получим 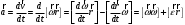 . Учитывая, что . Учитывая, что 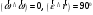 , получим связь линейного и углового ускорений , получим связь линейного и углового ускорений 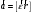 . .Линейные и угловые величины определяются аналогично. 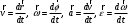 , , 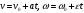 , , 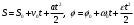 Как рассчитывается работа сил при вращательном движении? Ответ: Поскольку взаимное расположение частиц твёрдого тела при вращении не изменяется, элементарная работа внешних сил над телом будет равна приращению кинетической энергии этого тела 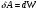 или или 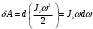 . Но . Но 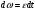 , следовательно , следовательно 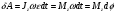 . Таким образом элементарная работа, совершаемая при вращении тела относительно неподвижной оси, равна произведению момента силы относительно оси вращения на элементарное угловое перемещение. . Таким образом элементарная работа, совершаемая при вращении тела относительно неподвижной оси, равна произведению момента силы относительно оси вращения на элементарное угловое перемещение.Работа на конечном угловом перемещении равна интегралу от элементарной работы, т.е. 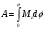 . Если момент силы с течением времени не изменяется, то . Если момент силы с течением времени не изменяется, то 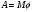 . .Как рассчитывается кинетическая энергия тела, вращающегося вокруг неподвижной оси? Ответ: Представим тело, вращающееся относительно оси z, как совокупность элементарных масс. Скорость i-й элементарной массы, находящейся на расстоянии r, от оси вращения, 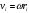 . .Её кинетическая энергия 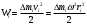 . А кинетическая энергия тела равна сумме кинетических энергий элементарных масс . А кинетическая энергия тела равна сумме кинетических энергий элементарных масс 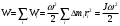 . .Как связаны кинетическая энергия тела и работа сил при вращательном движении? Ответ: Поскольку взаимное расположение частиц твёрдого тела при вращении не изменяется, элементарная работа внешних сил над телом будет равна приращению кинетической энергии этого тела 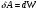 или или 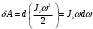 . .Как связаны вектор момента импульса и вектор момента силы при вращательном движении тела? Ответ: Возьмём производную по времени от выражения, определяющего момент импульса: 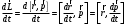 . Член . Член 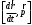 равен нулю, так как угол между векторами равен нулю, так как угол между векторами 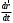 и и 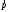 равен нулю. Производная импульса по времени, имеющаяся во втором члене полученного выражения, равна силе (второй закон Ньютона). Поэтому можем записать полученное выражение в следующей форме: равен нулю. Производная импульса по времени, имеющаяся во втором члене полученного выражения, равна силе (второй закон Ньютона). Поэтому можем записать полученное выражение в следующей форме: 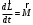 . т.е. скорость изменения момента импульса частицы равна моменту силы, действующему на эту частицу. . т.е. скорость изменения момента импульса частицы равна моменту силы, действующему на эту частицу.Проекция последнего уравнения на ось z выражает связь момента импульса относительно оси z и момента силы относительно той же оси. 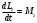 |
