|
Оқушылар екі топқа бөлінеді. Әр топ өз қасиетін дәлелдейді:
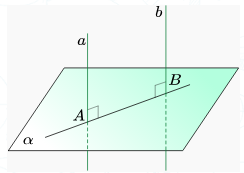
Теорема (1-қасиет). Егер параллель түзулердің біреуі жазықтыққа перпендикуляр болса, онда екіншісі де жазықтыққа перпендикуляр болады.
Егер a || b, a ⊥ α, онда b ⊥ α.
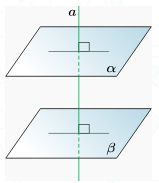
Теорема (2-қасиет). Егер екі жазықтық түзуге перпендикуляр болса, онда олар параллель болады.
Егер a ⊥ α, a ⊥ β, онда α || β.
|
|
|
Жұптасып, не үштікте жұмыс жасау.
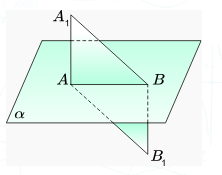
Символдар арқылы берілген AA1BB1 төртбұрышының түрін анықта.
AA1 ⊥ α; A ∈ α, B ∈ α; AA1 ≠ BB1, AB1 || A1B;
AA1 ⊥ α; BB1 ⊥ α; A ∈ α, B ∈ α, A1B =AB1;
A ∈ α; B ∈ α; AA1 ⊥ α; BB1 ⊥ α; AA1 =BB1.
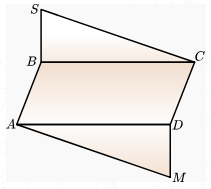
BCD – тіктөртбұрыш, BS⊥AB, AM⊥CD болсын. AMD және BSC жазықтықтары қалай орналасқанын тап.
|
|
|
Қалыптастырушы бағалауға арналған тапсырмалар
𝐴𝐵 кесіндісі 𝛼 жазықтығын қимайды. 𝐴𝐶 және 𝐵𝐷 түзулері осы жазықтыққа перпендикуляр және жазықтықты 𝐶 және 𝐷 нүктелерінде қиып өтеді. 𝐵𝐷 = 14,𝐶 = 34,𝐶𝐷 = 15. 𝐴𝐵-ның ұзындығын тап.
𝐴𝐵 кесіндісі 𝛼 жазықтығын 𝑂 нүктесінде қиып өтеді. 𝐴𝐶 және 𝐵𝐸 осы жазықтыққа перпендикуляр. 𝐵𝐸 = 12, 𝐴𝐶 = 6, 𝑂𝐸 = 9. 𝐴𝐵-ны тап.
𝐴𝐵𝐶 үшбұрышында ∠𝐶 = 120°. 𝐶𝐷 түзуі 𝐴𝐵𝐶 үшбұрыш жазықтығына перпендикуляр. Егер 𝐴𝐷 = 4√5,𝐷 = 10,𝐶𝐷 = 8 болса, 𝐴𝐵-ны тап.
𝐴𝐵𝐶𝐷 ромб жазықтығында ұзындығы 11 см болатын 𝐷𝐹 перпендикуляры жүргізілген. Егер ∠𝐵𝐴𝐷 = 120° және ромбтың қабырғасы 8 см болса, 𝐹 нүктесінен ромбтың диагоналдарының қиылысу нүктесіне дейінгі қашықтықты тап
|
| |
 Скачать 92.24 Kb.
Скачать 92.24 Kb.