|
|
аапап. Оушылара арналан баыт параы
Оқушыларға арналған бағыт парағы
10 сынып (жаратылыс тану бағыты)
Пәні
|
Алгебра және анализ бастамала
|
Мұғалімнің аты-жөні
|
Райпова Ә
|
оқулық
|
Алгебра және анализ бастамалары 2 бөлім
Авторы:А.Е.Әбілқасымова. Т.П.Кучер
|
Сабақтың тақырыбы
№ 1 сабақ(4 тоқсан ) ,
|
Функцияның өсу және кему белгілері
|
Оқыту мақсаттары
|
10.4.1.26 - интервалда функцияның өсу (кему) қажетті және жеткілікті шартын білу;
10.4.1.27-функцияның өсу (кему) аралығын табу;
|
Оқушының аты-жөні (оқушымен толтырылады)
|
Дулат Қадырғалиев
|
Іс-әрекет реті
|
ресурстар
(мұғалім толтырады)
|
(оқушы толтырады)
|
|
|
|
|
|
|
|
|
|
Жауап бер
|
1.Формулаларды қайталау, туындыны есептеу ережесі (оқулық), дәптердегі анықтамалық бойынша
2.Функциялардың туындысын есептеу:
1) 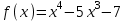 , 2) , 2) 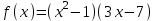 , ,
3) 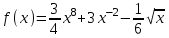 , 4) , 4) 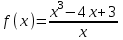 , ,
5) 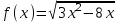 , ,
|
1.Екі функцияның қосындысының (айырмасының)туындысы туындылардың қосындысына (айырмасына) тен:(f(x)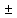 g(x))’=f’(x) g(x))’=f’(x)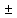 g’(x) g’(x)
2,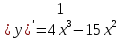
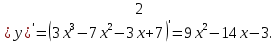
3)y’=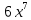 - 6x - - 6x - 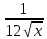
4)y’=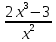
5)y’=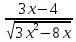
|
Мағынаны таны
|
Конспект
Функцияның кему, өсу аралықтарын табу алгоритмін жазыңыз:
1.Анықтау саласы
2. Туынды табу
3.Функцияның кему, өсу жағдайын тексеру(f|(x)>0-функция өседі, f/(x)<0 функция жойылады.
Функцияның кему, өсу аралықтарын табу алгоритмін жазыңыз:
1.Анықталу облысы
2. Туынды табу
3.Функцияның кему, өсу жағдайын тексеру
(f|(x)>0-функция өседі, f/(x)<0 функция кемиді.).
Мысалы: у=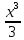 -4х2+7х-8 функциясының өсу,кему аралығын табу керек. -4х2+7х-8 функциясының өсу,кему аралығын табу керек.
Шешімі:
D (у)=R (анықтау саласы –барлық нақты сандар)
Туынды табамыз: у/=х2+8х+7
Теңсіздікті шешеміз: у / >0 (өсу аралығын табамыз): х2+8х+7>0
Ол үшін х2+8х+7=0 теңдеуін шешеміз :
D=64-4*1*7=36
х1=-7; х2=-1 квадрат үшмүшеге жіктеп жазсақ:
(х+7) (х+1) >0
Теңсіздікті интервал әдісімен шешеміз:
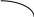 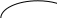
+ - +
   х х
-7 -1
Осылайша, функция аралықта өседі : Кемиді:(-7;-1)
|
Отметь знаком «+» материал, с которым ознакомился(лась)
+
|
Жауап бер
|
1.Функцияның өсу және кемуінің жеткілкті шарттарын атаңыз,ол
қандай.
2.Функцияның өсу және кему аралығын табу алгоритмін айтыңыз
|
1.Егер дифференциалданатнын y=f (х) функцияның туындысы Х аралағының әрбір нүктесінде f’(x)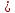 0(f’(x) 0(f’(x)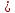 0) болса,онда функция сол Х аралағында өспелі (кемімелі) болады. 0) болса,онда функция сол Х аралағында өспелі (кемімелі) болады.
2.1)функция анықталу обылысын табу;
2)f(x) функция туындысын табу;
3)f’(x)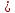 0 немесе f’(x) 0 немесе f’(x) 0 теңсіздігін шешу; 0 теңсіздігін шешу;
4)берілген теорема бойынша f(x) функциясының өсу және кему аралыұтарын табу.
|
Орында
|
№47.2(суретпен жұмыс)
№47.4(2,4)
№47.14(3,4)
|
|
Рефлексия
|
Мен бүгін + білдім
|
+ немесе – белгілерін қой
|
Мен енді - білемін
(бағалау критерийлеріне сәйкес)
|
|
Мұғалімнен кері байланыс
(ауызша кері байланыс немесе жазбаша ұсыныс
|
Орындалған тапсырмаларды дәптерге түсіріңіз
Маған WhatsApp-қа жіберіңіз немесе Kundelik.kz тиісті бөлімдегі порталға жүктеңіз
|
№47.3
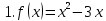
D(x)=R
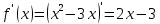
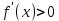 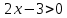
2x>3 - +

x>1,5 °
1,5
Ж/ы: 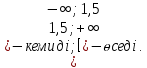
№47.14
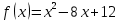
D(x)=R
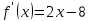
 
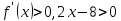
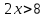 - + - +

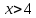 ° °
 4 4
Ж/ы: 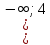 - - 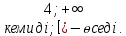 |
|
|
 Скачать 54.64 Kb.
Скачать 54.64 Kb.
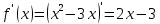

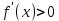
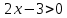

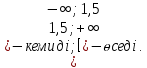
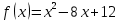
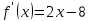


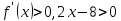
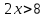 - +
- +
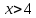 °
° 4
4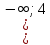 -
-