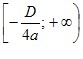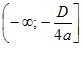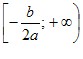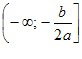кавадрадична. 11.Квадратична функція. Означення. Функцію, яку можна задати формулою виду yax2
 Скачать 146 Kb.
|
|
Квадратична функція, її графік і властивості Означення. Функцію, яку можна задати формулою виду y=ax2+bx+c, де a, b і c — деякі числа, причому a0, x — незалежна змінна, називають квадратичною. Квадратична функція не є для вас новою. Так, у 8 класі ви вивчали її частково — функцію y = x2. Функціональна залежність площі S круга від його радіуса r визначає квадратичну функцію S(r) = r2, яка в свою чергу є окремим видом функції y = ax2. На уроках фізики ви ознайомилися з формулою h = v0t –  , яка визначає залежність висоти h, на якій знаходиться тіло, що кинули вертикально вгору з початковою швидкістю v0, від часу руху t. Ця формула задає квадратичну функцію h(t) = v0t –  .Покажемо, як графік квадратичної функції y = ax2 + bx + c можна отримати з графіка функції y = ax2. Ви вже будували графіки функцій виду y = ax2 + bx + c, виділяючи квадрат двочлена (див. приклад 3 модуля 9). Використаємо цей прийом у загальному вигляді. Маємо: ax2 + bx + c = 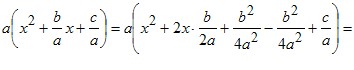 = 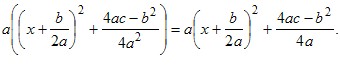 Введемо позначення 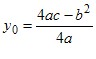 ,  .Тоді формулу y = ax2 + bx + c можна подати у вигляді: y = a(x – x0)2 + y0. Отже, схема побудови шуканого графіка є такою:
Графіком функції y = ax2 + bx + c є парабола з вершиною в точці (x0; y0), де 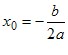, , 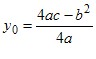яка дорівнює параболі y = ax2.Зрозуміло, що вітки параболи y = ax2 + bx + c направлені так само, як і параболи y = ax2: якщо a > 0, то вітки параболи направлені вгору, якщо a < 0, то вітки параболи направлені вниз. Загальне уявлення про графік квадратичної функції дають координати вершини параболи і напрям її віток. Це уявлення буде тим повнішим, чим більше точок, які належать графіку, ми знатимемо. Тому, не використовуючи зсувів, можна побудувати графік квадратичної функції за такою схемою: 1) знайти абсцису вершини параболи за формулою 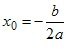 ;2) за формулою 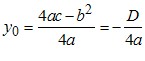 , де D — дискримінант квадратного тричлена ax2 + bx + c, знайти ординату вершини параболи і позначити на координатній площині вершину;(примітка. Формулу 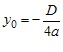 запам’ятовувати необов’язково. Достатньо обчислити значення функції y = ax2 + bx + c в точці з абсцисою 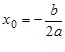 );3) визначити напрям віток параболи; 4) знайти координати ще кількох точок, які належать шуканому графіку (зокрема, координати точки перетину параболи з віссю y та нулі функції, якщо вони існують); 5) позначити на координатній площині знайдені точки і сполучити їх плавною лінією. У таблиці наведено деякі властивості квадратичної функції y = ax2 + bx + c.
Приклад. Побудуйте графік функції f(x) = x2 + 4x – 5. Користуючись графіком функції, знайдіть область значень функції, проміжки зростання і спадання, проміжки знакосталості, найменше і найбільше значення функції. Розв’язання. Дана функція є квадратичною функцією y = ax2 + bx + c, a = 1, b = 4, c = –5. Її графіком є парабола, вітки якої напрямлені вгору (a > 0). Абсциса вершини параболи x0 = –  = – = –2, ордината вершини y0 = f(x0) = f(–2) = 4 – 8 – 5 = –9. Отже, точка (–2; –9) — вершина параболи. Знайдемо точки перетину параболи з віссю абсцис: x2 + 4x – 5 = 0; x1 = –5, x2 = 1. Отже, парабола перетинає вісь абсцис у точках (–5; 0) і (1; 0). Знайдемо точку перетину параболи з віссю ординат: f(0) = –5. Парабола перетинає вісь ординат у точці (0; –5). Позначимо знайдені чотири точки параболи на координатній площині: 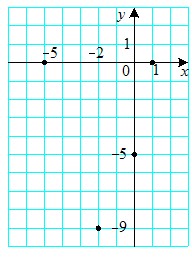 Тепер зрозуміло, що зручно знайти значення даної функції в точках –1, –3, – 4 і, позначивши відповідні точки на координатній площині, провести через усі знайдені точки графік даної функції. Маємо: f(–3) = f(–1) = –8; f(– 4) = f(0) = –5. Шуканий графік зображено на рисунку : 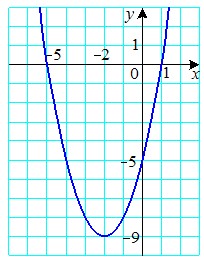 Область значень функції E(f) = [–9; +). Функція зростає на проміжку [–2; +) і спадає на проміжку (–; –2]. f(x) > 0 при x < –5 або x > 1; f(x) < 0 при –5 < x < 1. Найменше значення функції дорівнює –9, найбільшого значення не існує. |
