ПК 2102. ПК(2102). П. Г. Колинько пользовательские контейнеры
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
4.2. Обработка результатов экспериментаПо результатам эксперимента выполняется регрессионный анализ: подбор уравнения регрессии, наиболее соответствующего полученным данным. Для выполнения этого пункта следует получить у преподавателя набор данных «stat», состоящий из программы RG41, файлов с примерами ее входа и выхода (in.txt, out.txt) и заготовки электронной таблицы EXAMPLE. Программа RG41представляет собой консольное Windows-приложение и запускается из-под интерфейса командной строки (CMD). В качестве аргумента программа принимает имя файла с результатами измерений. Имя и расширение этого файла могут быть любыми. Рекомендуется поместить программу и файл измерений в один каталог. Если файл назван «IN.txt», строка запуска будет выглядеть таким образом: RG41 in.txt В программе RG41 имя входа «in.txt» принято по умолчанию и его можно опустить. В этом случае программу можно запускать и в окне проводника. Каждая из строк содержит результат одного опыта: размер входа и время, разделенные хотя бы одним пробелом. Упорядочивать данные по размеру входа необязательно. Можно выполнить по несколько опытов для некоторых или для всех размеров входа. Программа подсчитает и использует фактически имеющееся количество результатов. Она откажется работать только в случае, если опытов менее 10. Программа RG41 выдаст на экран значения коэффициентов регрессии для набора функций, начиная от константы (отсутствие регрессии) и кончая полиномом четвертой степени. Общий вид уравнения регрессии выводится программой в первой строке. Далее выводятся результаты подбора с поочередным подключением коэффициентов слева направо. Не используемые в уравнении коэффициенты выводятся нулями. Кроме коэффициентов дается значение выборочной дисперсии (и среднеквадратичного отклонения — СКО). Последняя колонка таблицы коэффициентов — оценочный код, вычисленных программой по результату сравнения отношения дисперсий с квантилем Фишера. Код состоит из двух символов — для допустимой ошибки 5% и 1%. Знак «+» указывает, что текущая модель может быть улучшена, знак «–» означает «нет». Недостоверные модели (с отрицательным старшим коэффициентом) обозначаются знаком «*». Результат работы программы RG41 включается в отчет в виде таблицы. Одновременно с выводом на экран программа RG41 создает текстовый файл OUT.txt, пригодный для импорта в электронную таблицу EXCEL. Для упрощения обработки результатов можно воспользоваться полученной у преподавателя заготовкой электронной таблицы EXAMPLE.xls. В эту таблицу импортируются файлы с результатами измерений и коэффициентами уравнений регрессии — ввод и вывод программы RG41. Данные из файлов помещаются на отведенные для них места. Вся необходимая обработка данных уже заложена в таблицу EXAMPLE. Содержимое файла с измерениями и файла OUT.txt нужно импортировать на свободное место в таблице (закладка «Данные», команда «Из текста»), а затем скопировать на штатное: измерения — в две крайние левые колонки, а коэффициенты уравнений регрессии — на соответствующее место в правой части (см. пример в табл. 4.1). Для корректного вида графиков измерения должны быть упорядочены по возрастанию мощности (выделить область с измерениями, в закладке «Данные» выполнить команду «А->Я»). Рядом с колонками результатов эксперимента находятся расчеты значений уравнений регрессии, по которым уже построены графики, а правее места расположения коэффициентов регрессии находится расчет отношений каждой выборочной дисперсии ко всем остальным (табл. 4.2). По значениям отношений дисперсий можно сразу указать наиболее подходящее уравнение регрессии, самый старший коэффициент которого определит временную сложность алгоритма. Наиболее подходящим будет то уравнение, при дальнейшем усложнении которого уменьшение выборочной дисперсии прекращается или перестает быть значимым.  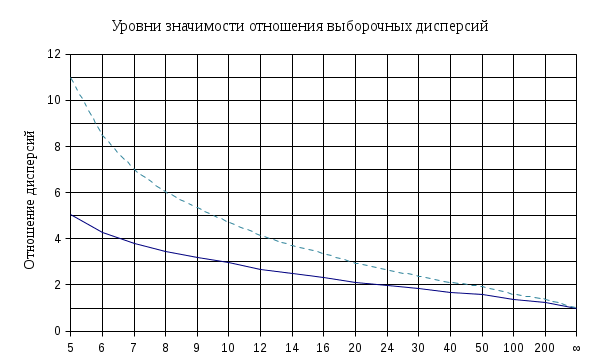 Степени свободы выборки Рис. 4.1. Квантили распределения Фишера Поскольку выборочные дисперсии являются случайными величинами, значения дисперсий можно считать различными только в том случае, если их отношение превосходит значение квантиля распределения Фишера (рис. 4.1). Входом в таблицу является количество степеней свободы выборки, равное количеству опытов минус количество оцениваемых коэффициентов регрессии. Во второй строке дано значение отношения выборочных дисперсий, которое можно считать значимым с ошибкой не более 5 %, в третьей — не более 1 %. Как видно из табл. 4.2, отношение дисперсий перестает быть значимым, начиная со строки 6 (квантиль Фишера для 100 опытов равен 1,39/1,59). Таблица 4.1.Пример результатов работы программы RG41 (100 точек)
Таблица 4.2Результаты расчета отношений выборочных дисперсий (фрагмент)
Если с учетом уровня значимости из всех полученных уравнений регрессии невозможно однозначно указать наиболее подходящее, следует попробовать увеличить количество опытов. При выборе подходящего уравнения регрессии следует также принимать во внимание следующие соображения:  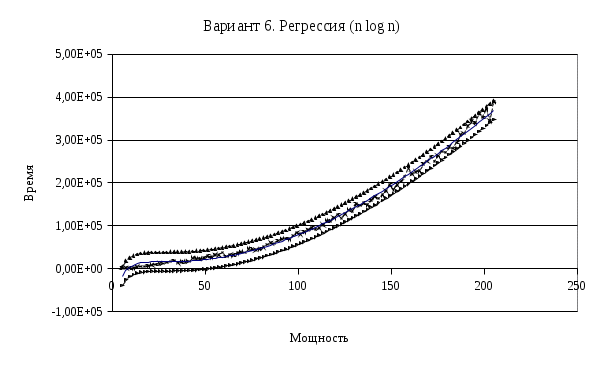 Рис. 4.2. Результат статистического эксперимента 1. Если базовой структурой данных является хеш-таблица, в уравнении регрессии неоткуда взяться логарифмам, и варианты с логарифмами принимать во внимание вообще не следует. Возможное исключение — использование сортировки в операции слияния. 2. Старший коэффициент корректного уравнения регрессии не может быть отрицательным. Такое уравнение не имеет физического смысла. Оно может получиться из-за смещения: отсчёты времени привязаны не к неправильному значению размера входа. Это может получиться, если используются размеры входа, заданные при генерации множеств, а не те, с которыми имеет дело каждая операция. Для нейтрализации смещения в примере программы эксперимента используется функция Used. Вызываемая после каждой операции с множествами, она подсчитывает их количество set_count и накапливает сумму мощностей middle_power, по которой в итоге вычисляется средняя мощность. 3. Необходимо также специально позаботиться о том, чтобы пересечения множеств были не пусты, а цепочка, исключаемая из последовательности операцией Excl, действительно в ней встречалась с достаточно большой вероятностью. В эксперименте это обеспечивается двумя вспомогательными функциями PrepareAnd и PrepareExcl. 4. Рекомендуется также перед экспериментом с измерением времени понаблюдать за результатами каждой из операций исследуемой цепочки, чтобы вовремя заметить и предотвратить вырождение (обработку пустых множеств и т. п.). Для этого в программе для эксперимента используется функция DebOut, выдающая результат на экран, если управляющая переменная debug имеет значение true. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
