Реферат парадокс случайных времен ожидания. Парадокс времени ожидания история парадокса
 Скачать 21.04 Kb.
|
|
ПАРАДОКС ВРЕМЕНИ ОЖИДАНИЯ ИСТОРИЯ ПАРАДОКСА Хотя современная технология постоянно уменьшает потери на время ожидания, они все еще существуют и во многом определяют нашу повседневную нервозность. Поэтому за попытками математиков и инженеров сократить время ожидания следят с большим интересом. А.Эрлангисследовал проблему времени ожидания для телефонных станций. В 30-е годы нашего века В.Феллерввел понятие процессов гибели и размножения, что придало новый импульс математическому анализу времени ожидания и во многом способствовало возникновению теории исследования операций. Изучение систем с очередями превратилось в независимую область науки на границе между теорией вероятностей и исследованием операций. ПАРАДОКС На автобусных остановках обычно указывается интервал движения автобуса, т. е. среднее время между двумя последовательными прибытиями автобусов. Предположим, что на некоторой автобусной остановке интервал движения составляет 10 мин. Тогда естественно считать, что люди ждут автобус в среднем 5 мин. Однако оказывается, что среднее время ожидания может не только превосходить 5 мин, но и быть бесконечным! (Опыт показывает, что в повседневной жизни ситуация не столь безнадежна. ОБЪЯСНЕНИЕ ПАРАДОКСА Если бы автобусы приходили на автобусную остановку не в только в среднем, но в точности каждые 10 мин, то среднее время ожидания в действительности равнялось 5 мин. Однако на самом деле автобусы ходят «партиями» (за исключением случая, когда мы находимся недалеко от автобусной станции, откуда автобусы отправляются). Следовательно, время ожидания имеет большой разброс относительно среднего значения. Предположим, что интервалы времени между последовательными прибытиями автобусов являются независимыми одинаково распределенными случайными величинами с математическим ожиданием m и стандартным отклонением s. Тогда можно показать, что среднее время ожидания равно 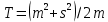 . Пусть F(t) – функция распределения и f(t) – плотность вероятности для интервалов времени между последовательными прибытиями автобусов. (Сейчас мы предположили существование плотности вероятности, однако от этого условия ценой некоторых изменений в рассуждениях можно отказаться). Пусть время tизмеряется от момента отправления последнего автобуса перед нашим приходом. Тогда плотность вероятности для случайного интервала времени до прибытия следующего автобуса равняется не f(t), а другой функции, пропорциональной tf(t), т. е. tf(t)/m, так как вероятность нашего появления в течение некоторого интервала времени пропорциональна его длине t. Таким образом, средне время ожидания Tвычисляется по формуле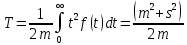 Плотность вероятности для нашел времени ожидания равна 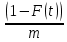 . Следовательно, T = m/2 только в случае s = 0, но если s = ∞, то и T = ∞. Эти крайние случаи, безусловно, далеки от реальности. В действительности интервалы между прибытиями автобусов имеют почти показательное («безвозрастное») распределение с некоторым параметром λ. Тогда m = s = 1/λ, т. е. T = m. Это означает, что если частота движения составляет 10 мин, то среднее время ожидания также равно 10 мин, а не 5 мин.Эвристическое объяснение этого парадокса довольно просто. Когда кто-то приходит на автобусную остановку в случайный момент времени, то имеет большие шансы ждать долго. Его время ожидания будет коротким, если он попадает на автобус из «партии», но автобусы в «партии» прибывают через малые интервалы, поэтому шансов успеть на один из них немного. Следовательно, если интервалы времени между последовательными прибытиями автобусов имеют большую дисперсию, то лишь немногие люди будут ждать мало, а большинство — в течение долгого времени. Это означает, что среднее время ожидания T велико. У нас часто возникает иллюзия, что куда бы нам ни надо было ехать, автобусы и трамваи чаще идут в противоположном направлении. В действительности это, естественно, невозможно. Объяснение очень простое. Мы видим только один автобус (на который мы сели) , едущий в нужном нам направлении, и в то же время положительна вероятность того, что, пока мы ждем, в противоположную сторону пройдут два или три автобуса. Их математическое ожидание равно 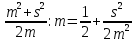 Что действительно больше 1/2, если sположительно. Отсюда вытекает асимметрия между двумя направлениями. Однако на самом делу это не так. Симметрия между двумя направлениями заключается в том, что вероятность того, что ни один автобус не проедет в противоположном направлении, пока мы ждем свои автобус, в точности равна 1/2 (но если один автобус пройдет в противоположном направлении, то могут пройти и несколько, поэтому возможно, что математическое ожидание будет как угодно большим). Пусть 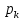 обозначает вероятность того, что, пока мы ждем, ровно k автобусов пройдут в противоположном направлении. Если интервалы между последовательными прибытиями автобусов имеют показательное распределение, то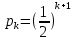 в случае равномерного распределения на интервале (0, 1) имеем 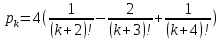 где k = 1, 2, … ( 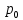 всегда равно 1/2, как мы уже отмечали).ЛИТЕРАТУРА Секей Г. Парадоксы в теории вероятностей и математической статистике: Пер. с англ. – М. Мир, 1990. |