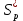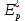Параллельное вычисление суммы числового ряда
 Скачать 53.98 Kb. Скачать 53.98 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования "Уфимский государственный авиационный технический университет" Кафедра Высокопроизводительных вычислительных технологий и систем Дисциплина: Основы суперкомпьютерных технологий и параллельное программирование. Отчет по лабораторной работе № 2 Тема: «Параллельное вычисление суммы числового ряда»
Уфа 2021 Цель: Научиться использовать принцип геометрической декомпозиции в параллельных алгоритмах и создавать параллельные программы для систем с распределенной памятью с использованием коллективных функций MPI на примере вычисления произведения двух матриц Теоретический материал: MPI - это стандарт на программный инструментарий для обеспечения связи между ветвями параллельного приложения. MPI предоставляет программисту единый механизм взаимодействия ветвей внутри параллельного приложения независимо от машинной архитектуры (однопроцессорные / многопроцессорные с общей/раздельной памятью), взаимного расположения ветвей (на одном процессоре / на разных) и API операционной системы. Параллельное приложение состоит из нескольких ветвей, или процессов, или задач, выполняющихся одновременно. Процессы обмениваются друг с другом данными в виде сообщений. Особенность MPI: понятие области связи (communication domains). При запуске приложения все процессы помещаются в создаваемую для приложения общую область связи. При необходимости они могут создавать новые области связи на базе существующих. Все области связи имеют независимую друг от друга нумерацию процессов. Программе пользователя в распоряжение предоставляется коммуникатор - описатель области связи. В исходных текстах примеров для MPI часто используется идентификатор MPI_COMM_WORLD. Это название коммуникатора, создаваемого библиотекой автоматически. Он описывает стартовую область связи, объединяющую все процессы приложения. Вариант №9 Задание: Требуется вычислить произведение матриц и и вычислить квадрат евклидовой нормы результирующей матрицы. Написать программу с использованием коллективных функций MPI В программе предусмотреть следующее: размерность L вводится пользователем (аргумент командной строки), размерность N=10L; матрицы заполняются случайными элементами вещественного типа; в) замер времени выполнения параллельной программы (вычисления + коммуникации). Запустить программу на кластере при числе процессов p = 1, 2, 4, 8, 16, 32, 64, 128, размерность подобрать так, чтобы время работы программы при p = 1 составляло около 60 и 600 с. Результаты замеров времени работы программы занести в таблицу. Вычислить ускорение и эффективность, построить их графики в зависимости от числа процессов. Составить отчет с оценкой полученных результатов. Выполнение: Выберем 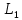 и и 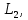 чтобы время работы программы при чтобы время работы программы при 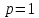 составляло порядка 60 и 600 секунд соответственно. Время работы параллельного участка кода занесем в таблицу: составляло порядка 60 и 600 секунд соответственно. Время работы параллельного участка кода занесем в таблицу:
Вычислим ускорение и эффективность при использовании p процессов по следующим формулам: 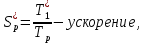 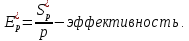 Построим графики зависимостей ускорения и эффективности от числа процессов при различном числе L.
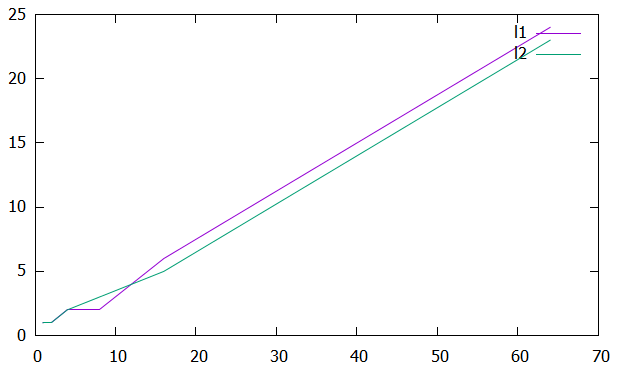 Рисунок 1 – График зависимости ускорения от числа процессов 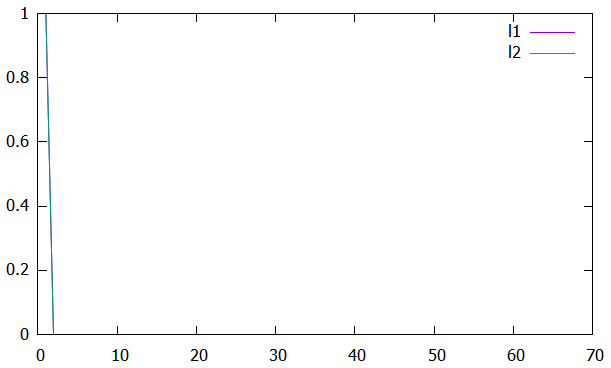 Рисунок 2 – График зависимости эффективности от числа процессов Из рисунков можно заметить, что ускорение увеличивается, а эффективность падает. Вывод: В ходе лабораторной работы научились использовать принцип геометрической декомпозиции в параллельных алгоритмах и создавать параллельные программы для систем с распределенной памятью с использованием коллективных функций MPI на примере вычисления произведения двух матриц. Было выявлено что ускорение увеличивается с ростом количества процессов, а эффективность падает. Приложение 1 #include "mpi.h" #include #include #include int main(int argc, char* argv[]) { int MyID, NumProc, ierror; double tstart, tfinish; MPI_Status status; ierror = MPI_Init(&argc, &argv); if (ierror != MPI_SUCCESS) { printf("MPI initialization error!\n"); } MPI_Comm_size(MPI_COMM_WORLD, &NumProc); MPI_Comm_rank(MPI_COMM_WORLD, &MyID); int N, L, Nc; L = atoll(argv[1]); N = 10 * L; Nc = (N / NumProc); if (MyID < (N % NumProc)) Nc++; double* A = new double[N * L]; double* An = new double[Nc * L]; double* B = new double[L * L]; double* C = new double[N * L]; double* Cn = new double[Nc * L]; int* displs = new int[NumProc]; int* scounts = new int[NumProc]; if (MyID == 0) { for (int i = 0; i < N * L; i++) { A[i] = 2.0 * (double)rand() / (double)RAND_MAX - 1.0; } for (int i = 0; i < L * L; i++) { B[i] = 2.0 * (double)rand() / (double)RAND_MAX - 1.0; } int count = N / NumProc, place = 0; int remainder; for (int i = 0; i < NumProc; i++) { if (i < (N % NumProc)) { remainder = 1; } else { remainder = 0; } displs[i] = place; scounts[i] = (count + remainder) * L; place += (count + remainder) * L; } } double norm = 0.0, total_norm = 0.0; MPI_Barrier(MPI_COMM_WORLD); tstart = MPI_Wtime(); MPI_Scatterv(A, scounts, displs, MPI_DOUBLE, An, Nc * L, MPI_DOUBLE, 0, MPI_COMM_WORLD); MPI_Bcast(B, L * L, MPI_DOUBLE, 0, MPI_COMM_WORLD); for (int i = 0; i < Nc; i++) { for (int j = 0; j < L; j++) { Cn[i * L + j] = 0.0; for (int k = 0; k < L; k++) { Cn[i * L + j] += An[i * L + k] * B[k * L + j]; } } } for (int i = 0; i < Nc * L; i++) { norm += Cn[i] * Cn[i]; } MPI_Reduce(&norm, &total_norm, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD); MPI_Gatherv(Cn, Nc * L, MPI_DOUBLE, C, scounts, displs, MPI_DOUBLE, 0, MPI_COMM_WORLD); MPI_Barrier(MPI_COMM_WORLD); tfinish = MPI_Wtime() - tstart; if (MyID == 0) { fprintf(stdout, "Norm: %lf\n", total_norm); fprintf(stdout, "Time: %lf\n", tfinish); } MPI_Barrier(MPI_COMM_WORLD); MPI_Finalize(); return 0; } | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 =2400
=2400