КОНТРОЛЬНАЯ РАБОТА № 3 ПО ТЕМЕ_ ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТ. Параллельность прямых и плоскостей

• Название: Параллельность прямых и плоскостей
• Дата: 20.11.2022
• Размер: 96.52 Kb.
• Имя файла: КОНТРОЛЬНАЯ РАБОТА № 3 ПО ТЕМЕ_ ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТ.docx
• Тип: Контрольная работа; #800984

Контрольная работа № 3

Тема: Параллельность прямых и плоскостей.

Вариант I

1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:

а) параллельными;

б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₂В₂, если А₁В₁ = 12 см, В₁О : ОВ₂ = 3 : 4.
3. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD₁.

1часть

1.В тетраэдре DАВС точки К,М,N,L – середины ребер AD,DB, BС, АC соответственно.

Докажите,что КМLN - параллелограмм.

2.Через конец А отрезка АВ проведена плоскость 𝛼. Через конец В и середину отрезка АВ – точку М проведены параллельные прямые, пересекающие плоскость 𝛼 в точках В₁ и М₁ соответственно. Найдите ММ₁, если ВВ₁ = 6см.

3.АВСD- параллелограмм. Точка Е не лежит в плоскости параллелограмма АВСD. АВЕ – треугольник. Докажите, что CD II (АВЕ).

2часть

4. Дан треугольник ВСЕ. Плоскость, параллельная прямой СЕ, пересекает ВЕ в точке М, а ВС – в точке Р. Найдите СР, если СЕ: РМ = 8 : 3, ВС=15.

5.Через точку P, не лежащую между двумя параллельными плоскостями 𝛼 и 𝛽, проведены две прямые, которые пересекают плоскость 𝛼 в точках A₁ и A₂, а плоскость 𝛽 − в точках B₁ и B₂. Найдите B₁B₂, если A₁A₂ = 6,5 м, PA₁ = A₁B₁.

Контрольная работа № 3

Тема: Параллельность прямых и плоскостей.

Вариант II

1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:

а) параллельными;

б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₁В₁, если А₂В₂ = 15 см, ОВ₁ : ОВ₂ = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K 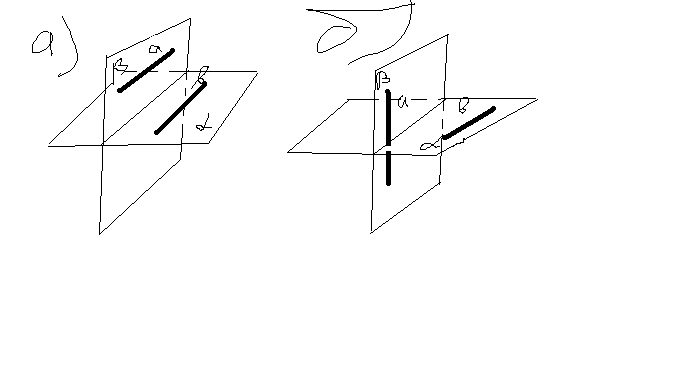DA, АK : KD = 1 : 3.




Задача

Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскость A и B в точках А1и А2 соответственно, прямая m - в точках В1 и В2. Найти длину отрезка А2В2, если А1В1 = 12см, В1О:ОВ2 = 3:4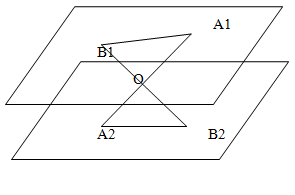 
 

Решение. 
Через прямые А1А2 и В1В2 можно повести плоскость, которая пересечёт параллельные плоскости по параллельным прямым А1В1 и А2В2. 
У образовавшихся треугольников ОА1В1 и ОА2В2 соответствующие углы равны. Углы при вершине О равны как вертикальные, а остальные - как внутренние накрест лежащие у параллельных прямых. Следовательно треугольники ОА1В1 и ОА2В2 подобны. 
У подобных треугольников соответствующие стороны соотностятся через коэффициент подобия. 
Откуда: 
ОВ1:ОВ2 = А1В1:А2В2, 
Следовательно: 
 А2В2 = 4 * 12 / 3 = 16 

Ответ: 16 см. 


1.
2. Треугольники ОА1В1 и ОА2В2 подобны. У подобных треуг-ков отношение соответствующих сторон сохраняется и оно равно 3/5. Тогда

ОВ1/ОВ2=3/5, соответственно А1В1/А2В2=3/5, тогда

А1В1/15=3/5

5*А1В1=45

А1В1=9см.

3.

Воспользуемся тем, что MN||BD и следовательно, KP||BD. находим точку P.

Или MK ∩ ABC = X, NX ∩ AB = P (метод следов). Точка P - найдена.

Сечение построено.