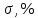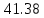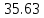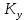праметрическая оптимезацыия. Мякошин_Параметрическая оптимизация следящей системы гидравличес. Параметрическая оптимизация следящей системы гидравлического усилителя руля автомобиля
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
Кафедра: «Автоматика и управление» Курсовая работа По дисциплине: «Проектирование автоматизированных систем». На тему : «Параметрическая оптимизация следящей системы гидравлического усилителя руля автомобиля» Группа: 151-212 Студент: Мякошин Н.А. Преподаватель: Кириличев Б.В. МОСКВА 2019 Содержание2. Выбор и описание системы управления. 2 2.2 Функциональная схема системы следящего рулевого привода автомобиля 5 2.3Блок-схема САР. 6 3.Математическое описание элементов САР 7 3.1 Усилитель 7 3.2 Золотник усилителя 7 3.3 Гидродвигатель 8 3.4 Колесная пара 8 3.5 Обратная связь 8 4. Структурная схема САР 8 5. Выбор варьируемых параметров 9 6.Получение передаточной функции замкнутой системы следящего рулевого привода автомобиля. 9 7.Моделирование исходной системы 10 8.Определение области работоспособности 11 9. Параметрическая оптимизация СУ 13 9.1. Выбор критериев оптимальности 13 9.2. Оптимизация по критерию «среднеквадратической ошибки» 13 9.3. Оптимизация по критерию «коэффициент перерегулирования» 15 9.5. Оптимизация по суперкритерию 18 9.6. Построение множества Парето 24 10. Выводы 26 11. 3D-моделирование элементов СУ 27 12. Список использованной литературы 29 2. Выбор и описание системы управления.В настоящее время сложно себе представить автомобиль, не оснащенный усилителем рулевого управления. Усилитель может быть электрическим (ЭУР), гидравлическим (ГУР) или электрогидравлическим (ЭГУР). Однако гидроусилитель рулевого управления остается наиболее распространенным типом на данный момент. Гидроусилитель руля (аббревиатура ГУР) — знакома большинству автолюбителей. Относится она к основной части рулевого механизма. Раньше управление машиной, было очень утомительным занятием, так как приходилось при резкой смене траектории напрягаться для поворота рулевого колеса, особенно это было проблематично на грузовых машинах. Чтобы свисти усилие водителя к минимуму, была придумана система гидроусилителя руля (рис 1.).  Рис.2. Гидроусилитель руля Основным его предназначением, как и было, задумано выступает, комфортное управление машиной в момент движения, но есть и другие не менее важные заслуги, такие как: сохранение «обратной связи» руля и колес; обеспечение устойчивости на дороге; повышение безопасности. То есть происходит контроль над транспортным средством после повреждения передней шины и возможность увильнуть от столкновения; позволяет «чувствовать» дорожное полотно и создает кинематическое следящее действие; уменьшает передаточное отношение рулевой системы, что повышает маневренность; продлевает время службы деталей рулевого узла. Гидроусилитель рулевого управления, состоит из: Силовой гидроцилиндр двойного действия помещен в рулевую часть, где стоит межу деталями привода и кузова. Соединен он с золотниковым управляющим узлом и гидроцилиндром. Основная заслуга — преобразование давления жидкости в перемещение поршня и штока, помогающих двигать колеса в необходимое направление. Насос прикрепляется на двигателе, а его привод от коленчатого вала осуществляется ременной передачей от шкива коленчатого вала. Требуется для сформирования давления масла. Более распространены конструкции лопастного типа, потому что у них хорошее КПД. Рабочая жидкость содержится в бачке, там же имеется фильтр, крышка с щупом для замера уровня. Функция масла смазывать трущиеся детали и передавать усилие от насоса к гидроцилиндру. Бачок, наполненный гидравликой, чтобы содержать его в чистоте внутри есть фильтр. Регулятор давления или распределитель – это прецизионный (высокоустойчивый) и простой по схеме узел. Являет собой редукционный клапан. Располагается на деталях рулевого привода или на одном валу с рулевым элементом. Его задача распределять гидравлику в нужную полость гидроцилиндра или назад в бак. Требуется для контроля частоты вращения коленвала мотора, чтобы тот не повышал допустимую норму давления гидравлической жидкости. Золотниковый распределитель – сложная деталь, состоящая из торсиона и золотникового клапана. Когда находящийся внутри золотник крутится, распределитель называют роторным, а если поступательно перемещается – осевым. Соединительные шланги высокого и низкого давления сводят между собой гидроцилиндр, насос и распределитель. Также по ним циркулирует гидравлическая жидкость из бака в насос и обратно, возвращаясь от распределителя. Там, где требуется создать взаимную подвижность узлов, применяют гибкие шланги. 2.2 Функциональная схема системы следящего рулевого привода автомобиля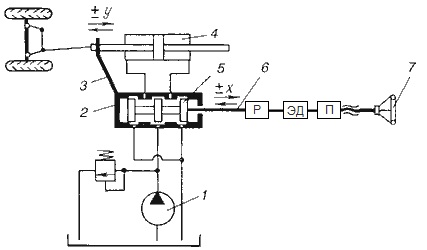 Рис2.2. Функциональная схема системы следящего рулевого привода автомобиля 1 - насос (внешний источник энергии); 2 - втулка усилителя; 3 - обратная связь; 4 - исполнительный механизм; 5 - золотник усилителя; 6 - винт; 7 - рулевое колесо (задающее устройство); Р – редуктор; ЭД – электродвигатель; П – потенциометр. При прямолинейном движении автомашины все элементы системы рулевого управления находятся в исходном положении. Жидкость из насоса 1 поступает к гидроусилителю золотникового типа. Золотник 5 усилителя занимает нейтральное положение, а в обеих полостях исполнительного механизма 4 установилось одинаковое давление. При необходимости изменить направление движения автомобиля водитель поворачивает рулевое колесо 7. Связанный с рулевым колесом винт 6 перемещает золотник усилителя на величину x, вызывая рассогласование в системе. При этом проходные сечения одних рабочих окон усилителя уменьшаются, а других увеличиваются. Это создает перепад давлений у исполнительного механизма, а его поршень приходит в движение, перемещаясь на величину y и поворачивая колеса автомобиля. Одновременно через обратную связь 3 движение поршня передается на втулку 2 усилителя. Совокупность 2 и 3 является сравнивающим устройством. Втулка перемещается в том же направлении, что и золотник 5 до тех пор, пока рассогласование в гидросистеме, вызванное поворотом рулевого колеса, не будет устранено. При непрерывном вращении водителем рулевого колеса поршень со штоком будет также непрерывно перемещаться, вызывая соответствующий поворот колес. При этом небольшие усилия водителя, прикладываемые к рулевому колесу, гидроприводом преобразуются в значительные усилия на штоке поршня, необходимые для управления автомобилем. 2.3Блок-схема САР.                    Р ЭД П У ЗУ ГД КП ОС – 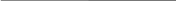 Рис.2.3. Блок-схема системы следящего рулевого привода автомобиля П – Потенциометр ЭД – Электродвигатель Р – Редуктор У – Усилитель ЗУ – Золотник усилителя ГД – Гидродвигатель КП – Колесная пара ОС – Обратная связь 3.Математическое описание элементов САР3.1 Усилитель Рис. 3.1. Схема усилителя В данной схеме используется также отрицательная ОС по напряжению, но она последовательная: здесь дифференциальное входное напряжение ОУ определяется как разность входного напряжения и напряжения обратной связи (сигнал подается непосредственно на не инвертирующий вход ОУ, а к инвертирующему входу подводится напряжение обратной связи с выхода ОУ). Поскольку напряжение между входами равно нулю, то на инвертирующем входе напряжение равно 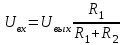 , ,таким образом, коэффициент усиления определяется формулой 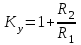 Следовательно, передаточная функция усилителя: 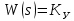 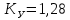 3.2 Золотник усилителяВ исполнительном устройстве с гидродвигателем управляющий ток преобразуется в перемещение золотника с помощью электрического устройства перемещения золотника. Все перечисленные процессы происходят довольно быстро. Поэтому передаточную функцию усилительно-преобразовательного устройства часто принимают в виде усилительного звена или апериодического звена с небольшой постоянной времени (несколько сотых долей секунды), т.е.: 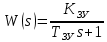 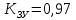 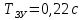 3.3 Гидродвигатель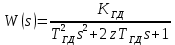 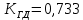 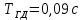 3.4 Колесная пара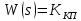 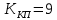 3.5 Обратная связьОбратная связь в рулевом приводе служит для построения привода как замкнутой автоматической системы с отрицательной обратной связью. Использование обратной связи позволяет улучшить качество регулирования в замкнутом приводе по сравнению с разомкнутым рулевым приводом, т. е. приводом без обратной связи. Технически обратная связь привода реализуется с помощью потенциометра обратной связи, который устанавливается на штоке поршня или непосредственно на руле. Математически обратную связь можно описать усилительным 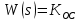 звеном с коэффициентом звеном с коэффициентом 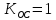 . .4. Структурная схема САРПо полученым передаточным функциям отдельных устройств получим структурную схему с описанием всех входящих в неё звеньев. 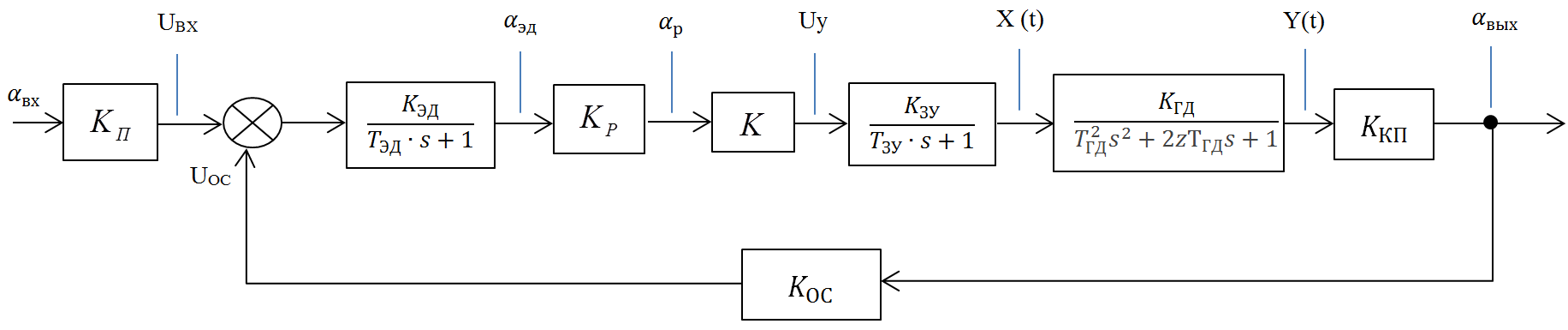 – Рис.4. Структурная схема системы следящего рулевого привода автомобиля 5. Выбор варьируемых параметровВ процессе проведения оптимизации данной системы изменениям следует подвергнуть только коэффициент передачи усилителя 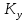 . Другие параметры будут оставаться неизменными, т.к. их варьирование связано с практическим неудобством их реального изменения в системе, которое может повлечь значительные конструктивные изменения. . Другие параметры будут оставаться неизменными, т.к. их варьирование связано с практическим неудобством их реального изменения в системе, которое может повлечь значительные конструктивные изменения.6.Получение передаточной функции замкнутой системы следящего рулевого привода автомобиля.Передаточная функция разомкнутой системы следящего рулевого привода автомобиля с учетом передаточных функций всех входящих в нее устройств будет иметь вид: 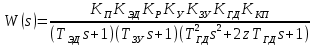 Передаточная функция замкнутой системы с учетом отрицательной обратной связи с коэффициентом 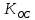 = = 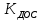 =1 будет иметь вид: =1 будет иметь вид: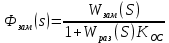 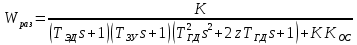 где 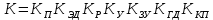 7.Моделирование исходной системыНа рис. 4 представлена структурная схема системы следящего рулевого привода автомобиля с описанием основных элементов системы в математической форме. Переходная функция исходной системы получена в ПК «МВТУ 3.7» и показана на рис. 7. 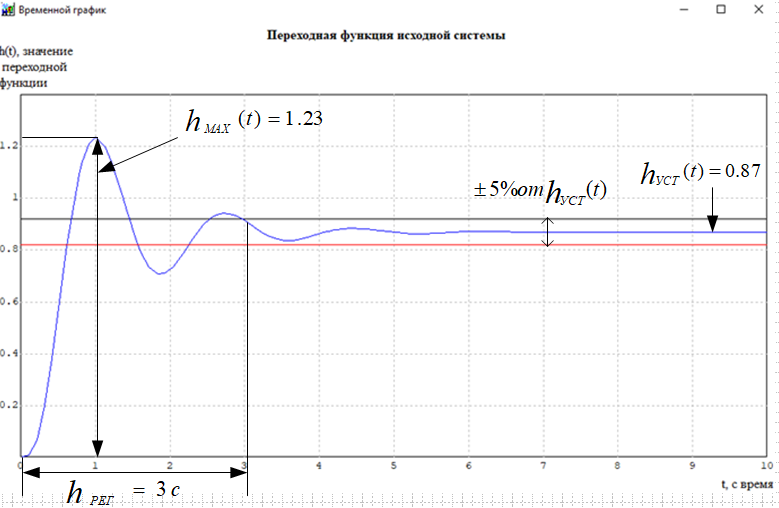 Рис. 7. Переходная функция исходной системы По графику переходного процесса определяем: Время регулирования, при котором кривая переходного процесса входит в 5%-ю трубку, определяя завершение переходного процесса (это время характеризует быстродействие системы): 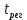 = 3c. = 3c. Коэффициент перерегулирования, который может служить мерой колебательности процесса: 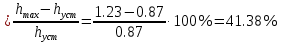 Коэффициент усиления: 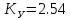 8.Определение области работоспособностиПоскольку условия работоспособности в задании не оговорены, то будем исходить из самых слабых возможных ограничений. Таковыми, как известно, являются требования устойчивости: если система становится неустойчивой – значит, она перестает быть работоспособной. Поэтому если из условия нахождения системы на границе устойчивости мы получим ограничения на варьируемые параметры, то это и позволит, по существу, определить одну из границ максимально возможной области работоспособности. Другие границы этой области можно определить из других разумных условий: например, обеспечения передачи информационных сигналов между устройствами системы и т.п. Итак, в рассматриваемой системе выбран один варьируемый параметр: коэффициент передачи усилителя 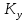 ., который входит как сомножитель в общий коэффициент передачи разомкнутой системы К. Для того чтобы составить характеристическое уравнение, необходимо приравнять знаменатель передаточной функции замкнутой системы к нулю: ., который входит как сомножитель в общий коэффициент передачи разомкнутой системы К. Для того чтобы составить характеристическое уравнение, необходимо приравнять знаменатель передаточной функции замкнутой системы к нулю: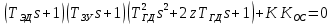 Раскрывая скобки и подставляя значения всех параметров, получим: 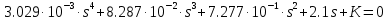 Введем обозначения: 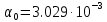 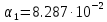 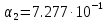 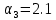 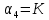 По коэффициентам этого уравнения составим определитель Гурвица и приравняем его к нулю, так как это соответствует границе устойчивости: Составляем матрицу коэффициентов характеристического уравнения исходной системы. 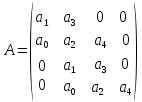 Для устойчивости системы необходимо что бы выполнялись условия: 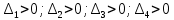 Составим определитель Гурвица и приравняем к нулю, так как это соответствует границе устойчивости. 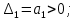 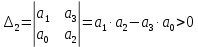 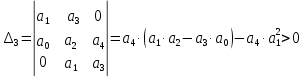 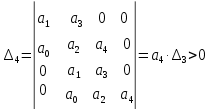 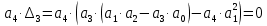 Для нахождения К достаточно вычислить определитель 3-го порядка: 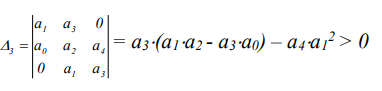 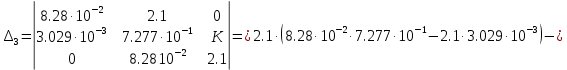 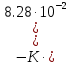 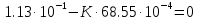 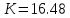 Теперь найдем 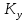 : : 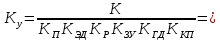 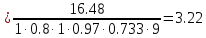 Поскольку варьируемый параметр всего один, то область работоспособности в этом частном случае представляет собой отрезок значений на действительной прямой, т.е. диапазон значений. Верхнее значение диапазона изменения параметра 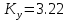 . . Нижнее значение диапазона определим из условия обеспечения передачи информации от устройства к устройству: неразрывности (прямой) цепи. Из этого условия следует, что коэффициенты передачи всех устройств, в том числе и усилителя, должны быть больше нуля. Если хотя бы один из них будет равен нулю, произойдет разрыв цепи, и информация не пройдет на выход системы. Зададим минимальное значение 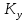 при исследовании системы. Возьмем при исследовании системы. Возьмем 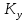 равным 0.1, т.к. при Ку =0 происходит разрыв системы. равным 0.1, т.к. при Ку =0 происходит разрыв системы.Таким образом, 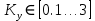 9. Параметрическая оптимизация СУ9.1. Выбор критериев оптимальностиПараметрическая оптимизация – это процедура нахождения значений внутренних параметров проектируемого или исследуемого объекта заданной структуры, при которых достигается наилучшее сочетание свойств этого объекта, отображаемое в критерии. Оптимальными называются те параметры, при сочетании которых вероятность выполнения условий работоспособности максимальна. Для нахождения оптимальных параметров системы требуется обеспечить экстремум критерия оптимальности (ЦФ), связанный с показателями динамического качества, за счет варьируемых параметров, допустимые значения которых лежат в заданной области. В качестве варьируемого параметра выбираем коэффициент передачи усилителя 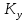 , с диапазоном изменения от 0,1 до 3. , с диапазоном изменения от 0,1 до 3.9.2. Оптимизация по критерию «среднеквадратической ошибки»Оптимизация проводилась по следующей схеме: 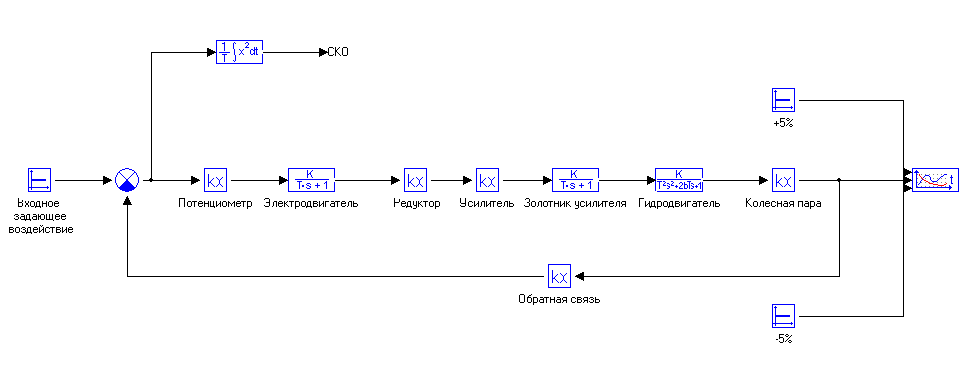 Рис. 9.2. Схема моделирования по критерию «среднеквадратическая ошибка» Целевая функция сформирована на выходе блока: 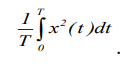 Целью оптимизации явилось нахождение минимального значения среднеквадратической ошибки. Коэффициент передачи усилителя 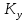 изменяем в пределах от 0,1 до 3. Оптимизация велась с интервалом неопределенных параметров = 0,1 изменяем в пределах от 0,1 до 3. Оптимизация велась с интервалом неопределенных параметров = 0,1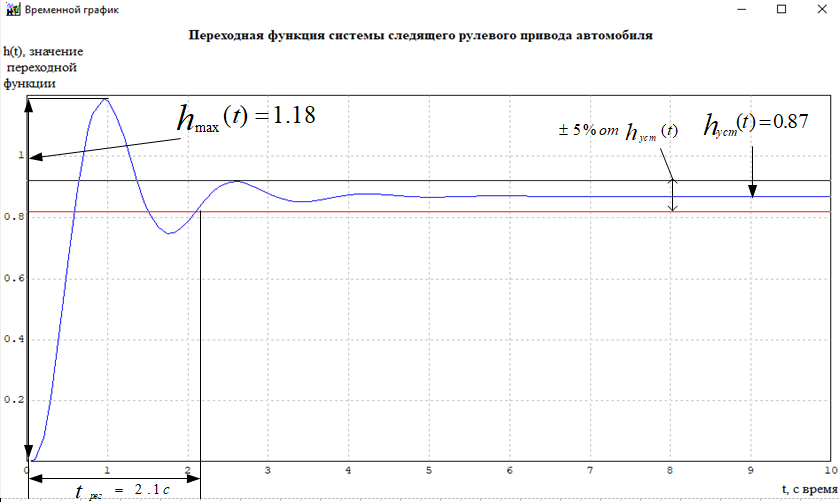 Рис. 9.3. Переходная характеристика для оптимизации по среднеквадратичной ошибке В результате оптимизации параметра 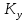 получили получили 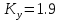 . Характеристики переходного процесса имеют следующие значения: . Характеристики переходного процесса имеют следующие значения:Время регулирования: 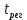 = 2.1c; = 2.1c; Коэффициент перерегулирования:  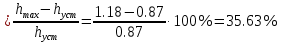 9.3. Оптимизация по критерию «коэффициент перерегулирования»Оптимизация проводилась по схеме, показанной на рис. 9.4. 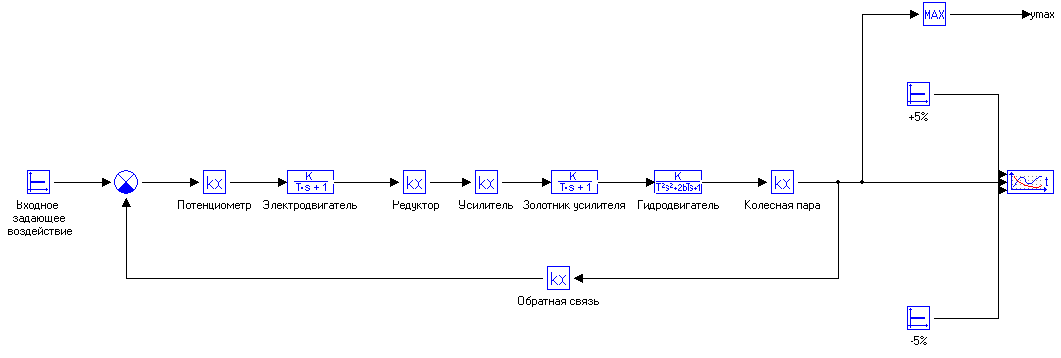 Рис. 9.4. Схема моделирования для оптимизации по критерию «перерегулирование» Цель оптимизации нахождение минимального значения коэффициента перерегулирования. Коэффициент усиления 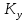 изменяем в пределах от 0,1 до 3,0. Оптимизация велась с интервалом неопределенных параметров = 0,01. изменяем в пределах от 0,1 до 3,0. Оптимизация велась с интервалом неопределенных параметров = 0,01.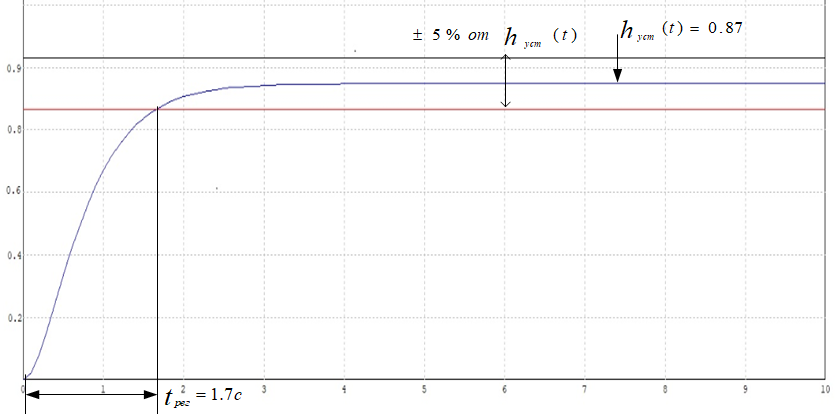 Рис. 9.5. Переходная характеристика для оптимизации по коэффициенту перерегулирования Рис. 9.5. Переходная характеристика для оптимизации по коэффициенту перерегулированияПри выполнении оптимизации были получены следующие результаты: Время регулирования: 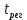 = 1.7; = 1.7;Коэффициент перерегулирования: = 0% 9.4. Оптимизация по критерию «минимум времени регулирования» Цель оптимизации нахождение минимального значения времени регулирования. Оптимизация проводилась по следующей схеме, показанной на рис. 9.6. 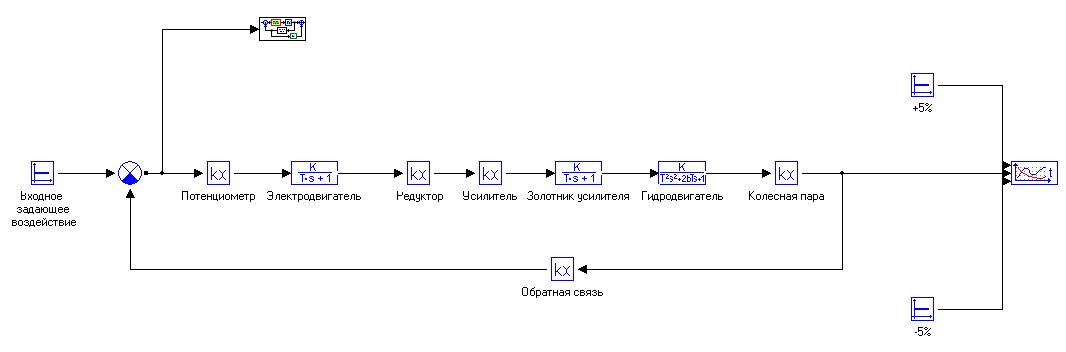 Рис. 9.6. Схема моделирования для оптимизации по времени регулирования Принцип действия схемы субмодели: На средний (логический) входной порт (величина «трубки») подается модуль сигнала рассогласования. Если этот сигнал больше уставки (5%), то на выход подается сигнал с 3-его (нижнего) входного порта, т.е. текущее модельное время. Если управляющий сигнал (на среднем входном порту) меньше уставки, то на выход передается сигнал с первого (верхнего) входного порта, т.е. тот же сигнал, но задержанный на один шаг интегрирования. Задержку на один шаг интегрирования осуществляет типовой блок с подписью «Время переходного процесса» (типовой блок «Задержка на шаг интегрирования» из библиотеки «Дискретные звенья»). 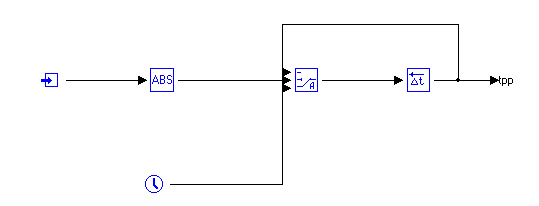 Рис. 9.7. Схема субмодели 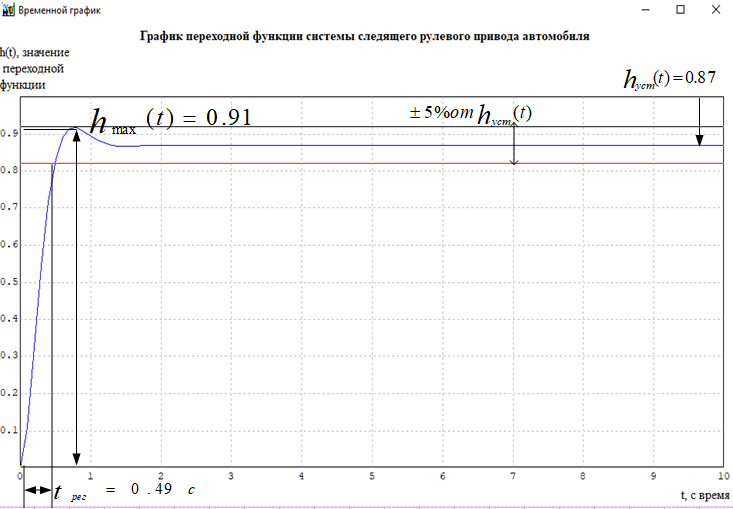 Рис. 9.8. Переходная характеристика для оптимизации по времени регулирования При выполнении оптимизации были получены следующие результаты: Время регулирования: 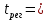 0,49c; 0,49c; Коэффициент перерегулирования: = 4.5%. 9.5. Оптимизация по суперкритериюЗадача оптимизации – многофункциональная задача, т.к. имеет более одного параметра, претендующего на роль критерия оптимальности. Используем аддитивный суперкритерий, объединяющий все выходные параметры (частные критерии) в одну целевую функцию, представляющую собой сумму частных критериев: 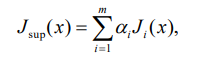 где 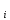 - относительный вклад частных критериев в суперкритерий; - относительный вклад частных критериев в суперкритерий;m - число выходных параметров. Для нашего случая аддитивный критерий будет выглядеть следующим образом: 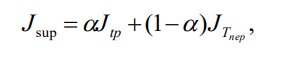 где α – весовой коэффициент. Оптимизация проводилась по следующей схеме: 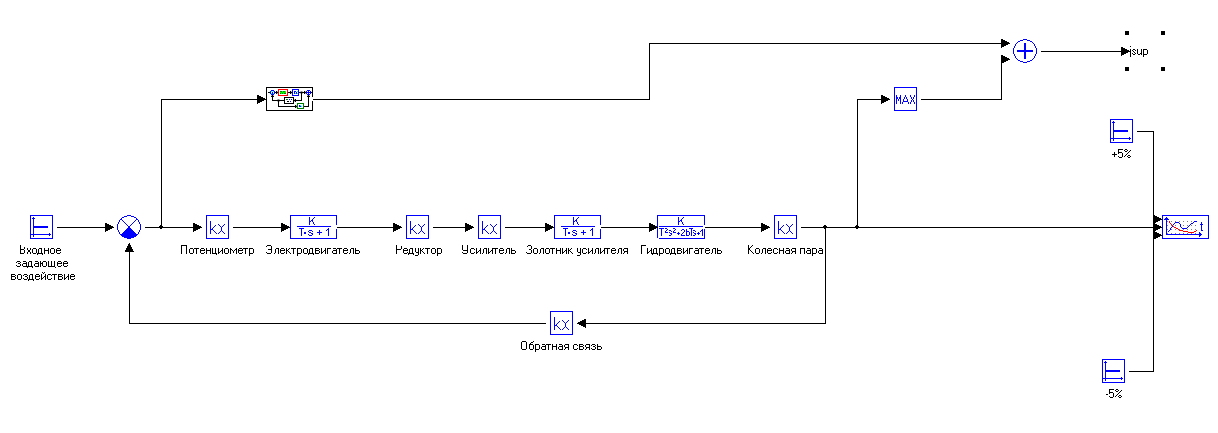 Рис. 9.9. Схема моделирования системы для оптимизации по «суперкритерию» При оптимизации по суперкритерию проводятся те же вычисления, что и для других методов, при каждом значении α (от 0 до 1, шаг 0,2). Результаты оптимизации: при =0 (Рис. 9.1.0)  Рис. 9.1.0. Результаты оптимизации при =0 При выполнении оптимизации были получены следующие результаты: Время регулирования: 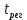 = 1.7; = 1.7;Коэффициент перерегулирования: = 0% При =0,2: 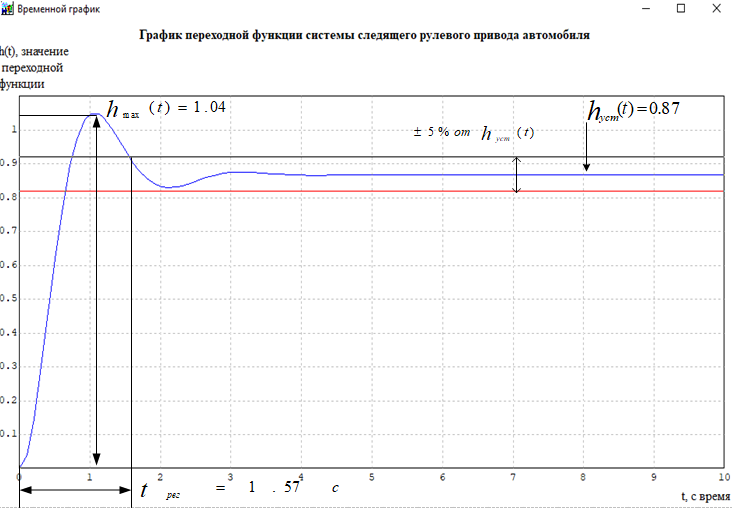 Рис. 9.1.1. Результаты оптимизации при =0.2 При выполнении оптимизации были получены следующие результаты: Время регулирования: 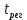 = 1.57; = 1.57;Коэффициент перерегулирования: = 19.5% При =0,4: 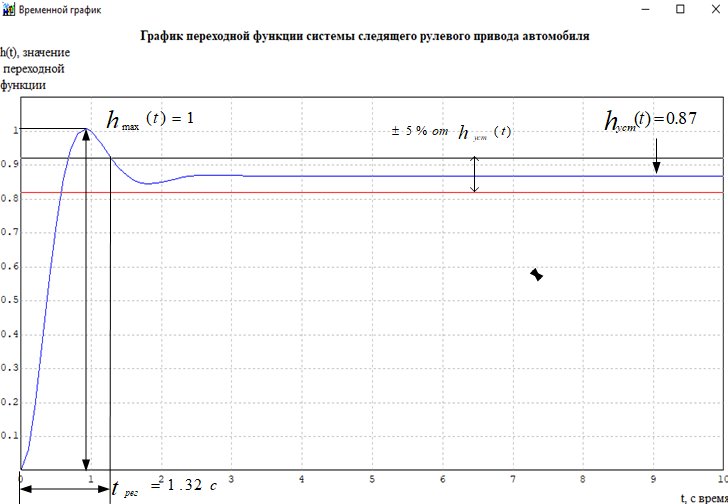 Рис. 9.1.2. Результаты оптимизации при =0.4 При выполнении оптимизации были получены следующие результаты: Время регулирования: 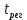 = 1.32; = 1.32;Коэффициент перерегулирования: = 14.9% При =0,6: 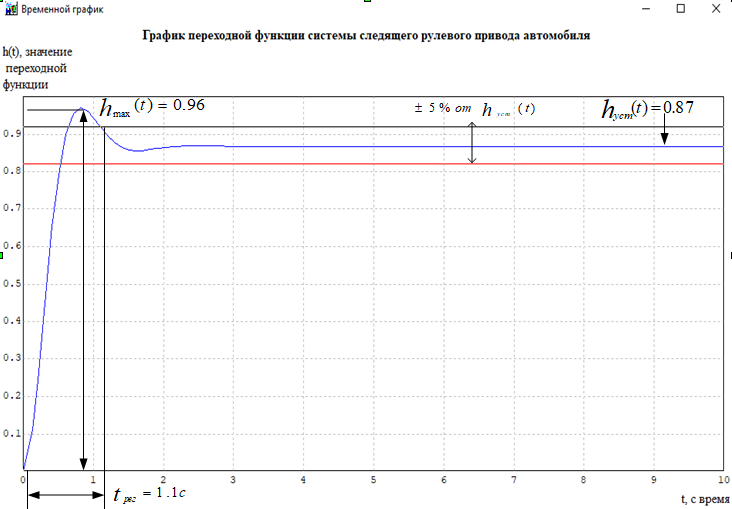 Рис. 9.1.3. Результаты оптимизации при =0.6 При выполнении оптимизации были получены следующие результаты: Время регулирования: 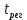 = 1.1; = 1.1;Коэффициент перерегулирования: = 10.3% При =0,8: 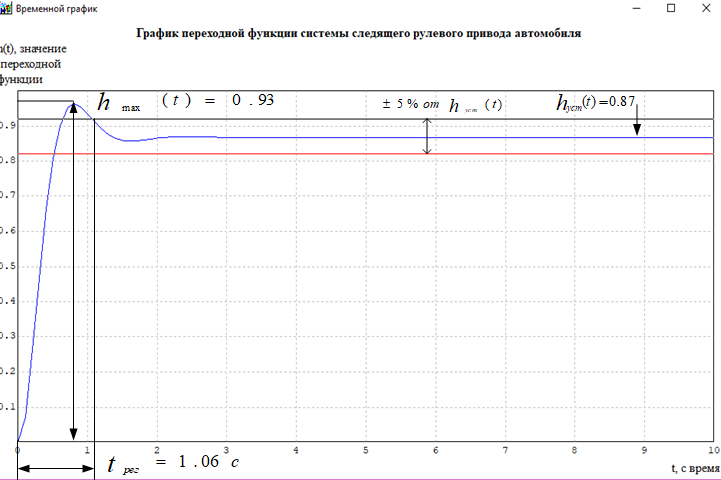 Рис. 9.1.4. Результаты оптимизации при =0.8 При выполнении оптимизации были получены следующие результаты: Время регулирования: 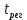 = 1.06; = 1.06;Коэффициент перерегулирования: = 6.89% При =1:  Рис. 9.1.5. Результаты оптимизации при =1 При выполнении оптимизации были получены следующие результаты: Время регулирования: 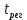 = 0.49; = 0.49;Коэффициент перерегулирования: = 4.5%. 9.6. Построение множества ПаретоСтроим график зависимости коэффициента перерегулирования (, %) от времени регулирования ( 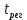 , с): , с):исходной системы; по среднеквадратической ошибке; по перерегулированию; по времени регулирования; по суперкритерию (подставляя в уравнение 1 разные значения от 0 до 1 с интервалом 0,2). Таблица 1
Получаем точки, плавно соединив которые, строим некую интерполяционную кривую (рис. 9.1.6). Множество точек этой кривой называется областью компромиссов или областью (множеством) Парето. 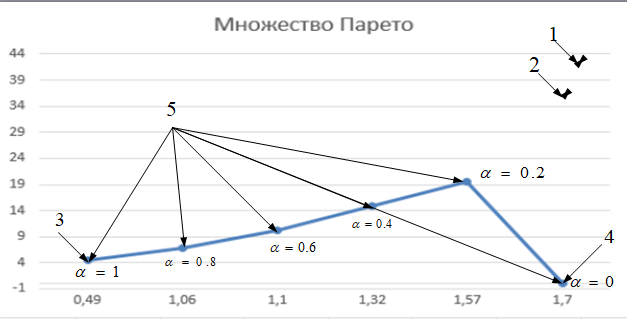 Рис. 9.1.6. « множество Парето» Результаты оптимизации в пространстве критериев 1-исходная система; 2-система, оптимизированная по критерию СКО; 3-система,оптимизированная по критерию «время регулирования»; 4-система, оптимизации по критерию «перерегулирование»; 5- система, оптимизированная по аддитивному суперкритерию 10. ВыводыВ процессе проделанной работы по исследованию системы стабилизации самолета по углу атаки, проведена многокритериальная параметрическая оптимизация. Для исследования использовались критерии: - среднеквадратическая ошибка (СКО); - перерегулирование; - время регулирования; - суперкритерий. Таблица 2
Вывод В процессе работы по исследованию системы управления линейной скоростью автомобиля, проведена многокритериальная параметрическая оптимизация. Для исследования использовались критерии: -Среднеквадратическая ошибка(СКО) -Перерегулирование -Время регулирование -Аддитивный суперкритерий Не выделив наилучшую альтернативу, то есть обладающую наименьшими значениями параметров, прибегли к методу нахождения множества Парето. Наилучшие результаты: При нулевом перерегулировании, время регулирования 2с, а при 5%-0,8с. Если нужны лучшие показатели, то параметрической оптимизации не достаточно, и следует прибегнуть к структурной оптимизации. Это потребует включения дополнительных динамических корректирующих звеньев. Таким образом, не меняя исходной системы, можно добиться разных результатов, в зависимости от того, какая цель преследуется при параметрической оптимизации. 11. 3D-моделирование элементов СУ Рис.11 «Шкив насоса ГУР» 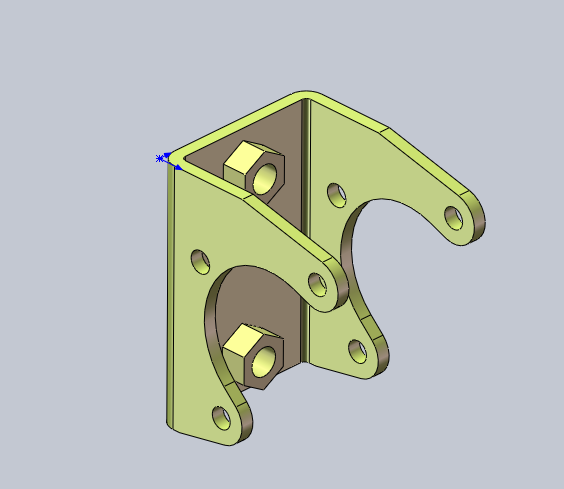 Рис.11.1. «Кронштейн насоса ГУР»  Рис.11.2 «Насос ГУР» 12. Список использованной литературы1. Проектирование автоматизированных систем: Курс лекций по дисциплине. Б.В. Кириличев. – М.: МГИУ, 2008. 2. Теория автоматического управления: Курс лекций по дисциплине. А.И. Мартяков. – М.: МГИУ, 2006. 3. http://autoleek.ru/hodovaja-chast/rulevoe-upravlenie/ustrojstvo-gidrousilitelya-rulya.html 4. https://ru.wikipedia.org/wiki/Гидроусилитель_руля | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

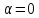
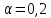
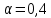
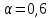
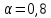
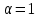
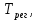 c
c