эконометрика 1 лаба. Парный корреляционный анализ проверка наличия и степени тесноты линейной и нелинейной связи
 Скачать 53.88 Kb. Скачать 53.88 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ Кафедра: «Информационные системы» Дисциплина: Эконометрика Лабораторная работа №1 Выполнила: студентка группы ИСЭбд-21 Шеронова А. Ю. Проверил преподаватель: Шанченко Н. И. Ульяновск 2020 г. Парный корреляционный анализ: проверка наличия и степени тесноты линейной и нелинейной связи.Вариант №1 Задание. На основании данных таблицы П1.1 для соответствующего варианта (табл. 1.3): Вычислить линейный коэффициент парной корреляции 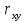 и индекс корреляции R. и индекс корреляции R.Проверить значимость коэффициента парной корреляции 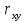 и индекса корреляцииR при уровне значимости α = 0,05 для нечетного варианта и α = 0,01 для четного варианта. и индекса корреляцииR при уровне значимости α = 0,05 для нечетного варианта и α = 0,01 для четного варианта.Построить доверительный интервал для значимого линейного коэффициента парной корреляции 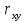 . .Исходные данные: переменные x и y задаются графами 1 и 2 таблицы П1.1; зависимости: линейная и 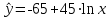 ; ;уровень значимости α = 0,05. Решение 1) Вычисление σx, σy и 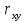 . Используя данные таблицы 1 получим . Используя данные таблицы 1 получимТаблица 1 Промежуточные результаты расчетов
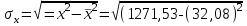 = 15,569, = 15,569,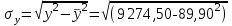 = 34,532, = 34,532,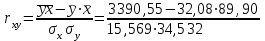 = 0,942. = 0,942.Вычисление R: 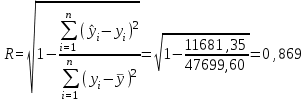 . . 2) Проверка значимости 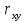 . .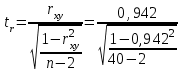 = 17,30. = 17,30.tкрит = t1-α,n-2 = СТЬЮДЕНТ.ОБР.2Х(0,05;38) =2,024. Так как 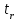 = 17,30 > t1-α,n-2 = 2,024, = 17,30 > t1-α,n-2 = 2,024,то делаем вывод о статистической значимости линейного коэффициента парной корреляции 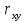 . .Проверка значимости индекса корреляции R. Значение F-критерия Фишера 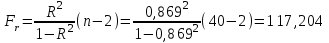 При α = 0,05 и степенях свободы k1 = 1, k2 = n - 2 = 40 – 2 = 38. Fкрит = F.ОБР.ПХ(0,05;1;38) = 4,098 Так как 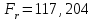 > Fкрит = 4,098, > Fкрит = 4,098,то формально с погрешностью 5% индекс корреляции следует считать значимым и следовательно с вероятность 95% нельзя отвергать наличие исследуемой зависимости. 3) Построение доверительного интервала для линейного коэффициента корреляции 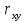 . .Определим величину z . Z-преобразования Фишера 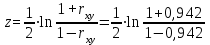 = 1,756. = 1,756.t1-α/2 = НОРМСТОБР(0,975) = 1,96. Вычислим 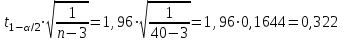 . .Вычислим границы доверительного интервала (z– , z+) для величины z 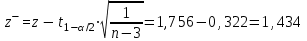 , ,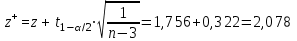 . .Определим граничные значения доверительного интервала (r– , r+) для rxy, используя статистическую функцию ФИШЕРОБР() из MS Excel. 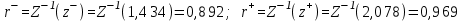 . .Искомый доверительный интервал для rxy имеет вид (0,892; 0,969). Результаты: 1) 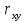 = 0,942. = 0,942. 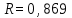 . . 2) Коэффициенты для rxy и R – статистически значимы. 3) Доверительный интервал для rxy – (0,892; 0,969). |

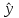
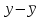 )
)