ответы по типс. Перечень вопросов по дисциплине Теория информационных процессов и систем

Название	Перечень вопросов по дисциплине Теория информационных процессов и систем
Анкор	ответы по типс
Дата	18.01.2023
Размер	158.93 Kb.
Формат файла
Имя файла	otvety.docx
Тип	Документы #892852
страница	3 из 4

1 2 3 4

ОСНОВНЫЕ ПАРАМЕТРЫ ПОЛОСЫ ПРОПУСКАНИЯ

Ширина полосы

Ширина полосы обычно определяется как разность верхней и нижней граничных частот участка АЧХ. Ширина полосы пропускания выражается в единицах частоты (например, в Гц). Расширение полосы пропускания позволяет передать большее количество информации.

Неравномерность АЧХ

Неравномерность АЧХ характеризует степень отклонения от прямой, параллельной оси частот. Неравномерность АЧХ выражается в децибелах.

Ослабление неравномерности АЧХ в полосе улучшает воспроизведение формы передаваемого сигнала.

Идеальные и реальные модели канала передачи информации.

ИДЕАЛЬНЫЙ КАНАЛ

Модель идеального канала используется тогда, когда можно пренебречь наличием помех. При использовании этой модели выходной сигнал является детерминированным, мощность и полоса пропускания сигналов ограниченны.

Детерминированный сигнал точно определен в любой момент времени.

Полоса пропускания это разность между максимальной и минимальной частотами сигнала.

РЕАЛЬНЫЙ КАНАЛ

В реальных каналах всегда имеются ошибки при передаче сообщений. Ошибки приводят к уменьшению пропускной способности канала и потере информации. Вероятности появления ошибок во многом определяются искажениями сигналов и влиянием помех.

Сигнал на выходе канала можно записать в следующем виде:

x(t) = μ(t)∙s(t-T)+w(t),

где s(t) – сигнал на входе канала, w(t) – аддитивная помеха, μ(t) – мультипликативная помеха, T – задержка сигнала.

Аддитивная помеха – помеха, прибавляемая к сигналу при передаче его по информационному каналу.

Аддитивные помехи обусловлены флуктуационными явлениями (случайными колебаниями тока и напряжения), связанными с тепловыми процессами в проводах, резисторах, транзисторах и других элементах схем, наводками под действием атмосферных явлений (грозовые разряды ит. д.) и индустриальных процессов (работа промышленных установок, других линий связи и т. д.).

Мультипликативная помеха – помеха, перемножаемая с сигналом.

Мультипликативные помехи обусловлены случайными изменениями коэффициента передачи канала из-за изменения характеристик среды, в которой распространяются сигналы, и коэффициентом усиления схем при изменении питающих напряжений, из-за замираний сигналов в результате интерференции и различного затухания сигналов при многолучевом распространении радиоволн. К мультипликативным помехам следует отнести и "квантовый шум" лазеров, применяемых в оптических системах передачи и обработки информации. "Квантовый шум" лазера вызван дискретной природой светового излучения и зависит от интенсивности излучения, т. е. от самого полезного сигнала.

Понятие о дискретизации и квантовании сигналов.

Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизацией.

Аналоговый сигнал – это сигнал, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений.

Дискретный сигнал – это сигнал, который принимает лишь конечное число значений.

Квантование - разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов.

Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике — по вертикали). Сигнал, к которому применены дискретизация и квантование, называется цифровым.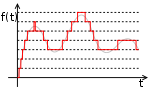

Рис.1 – квантованный сигнал.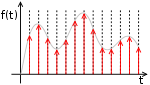

Рис.2 – неквантованный сигнал с дискретным временем.

Цифровой сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.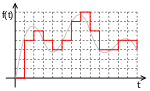

Рис3. – цифровой сигнал.

Классификация методов дискретизации сигналов.

Используется дискретизация по времени и по уровню.

ДИСКРЕТИЗАЦИЯ ПО ВРЕМЕНИ

Дискретизация по времени выполняется путем взятия отсчетов функции в определенные дискретные моменты времени. В результате непрерывная функция заменяется совокупностью мгновенных значений.

Равномерная дискретизация

Моменты отсчета выбираются на оси времени равномерно. Теорема Котельникова – если аналоговый сигнал имеет ограниченный по ширине спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой, строго большей удвоенной верхней частоты.

Адаптивная дискретизация

Вследствие того, что изменение функции различно в различные моменты времени, шаг дискретизации может быть различным, обеспечивая равномерную погрешность на каждом шаге.

ДИСКРЕТИЗАЦИЯ ПО УРОВНЮ

Дискретизация значений функции (уровня) носит название квантования. Операция квантования сводится к тому, что вместо данного мгновенного значения сообщения передаются ближайшие значения по установленной шкале дискретных уровней.

Дискретные значения по шкале уровней чаще всего выбираются равномерно. При квантовании вносится погрешность (искажение), так как истинные значения функции заменяются округленными значениям. Величина этой погрешности не превосходит половины шага квантования и может быть сведена до допустимого значения. Погрешность является случайной функцией и проявляется на выходе как дополнительный шум ("шум квантования"), наложенный на передаваемое сообщение.

ДИСКРЕТИЗАЦИЯ ПО ВРЕМЕНИ И УРОВНЮ

Позволяет непрерывное сообщение преобразовать в дискретное (аналоговый сигнал в цифровую форму), которое затем может быть закодировано и передано методами дискретной (цифровой) техники.

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ

Дискретизированный сигнал можно рассматривать как результат умножения первоначального непрерывного сигнала на ряд единичных импульсов.

Критерии оценки точности дискретизации сигналов.

Разность между истинными значениями сигнала x(t) и приближающей P(t), или воспроизводящей V(t) - функцией, представляет собой текущую погрешность дискретизации или соответственно восстановления:

Выбор критерия оценки погрешности дискретизации (и восстановления) сигнала осуществляется получателем информации и зависит от целевого использования дискретизированного сигнала и возможностей аппаратной (программой) реализации. Оценка погрешности может проводиться как для отдельных, так и для множества реализаций сигнала.

Чаще других отклонение воспроизводимой функции V(t) от сигнала x(t) на интервале дискретизации Δt_i = t_i – t_i_–1 оценивается следующими критериями.

а) Критерий наибольшего отклонения:

где ε(t) – текущая погрешность, определяемая выражением (1).

б) Среднеквадратический критерий, определяемый следующим выражением: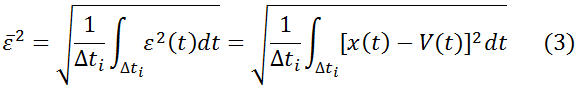

где ε(t) – текущая погрешность (1).

Черта сверху означает усреднение по вероятностному множеству,

в) Интегральный критерий как мера отклонения x(t) от V(t) имеет вид: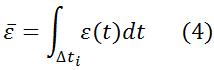

г) Вероятностный критерий определяется соотношением:

где ε₀ – допустимое значение погрешности;

Р₀ – допустимая вероятность того, что погрешность не превышает значениеε₀.

Равномерная дискретизация. Теорема Котельникова.

Дискретизация по времени выполняется путем взятия отсчетов функции в определенные дискретные моменты времени. В результате непрерывная функция заменяется совокупностью мгновенных значений.

Равномерная дискретизация

Моменты отсчета выбираются на оси времени равномерно. Теорема Котельникова – если аналоговый сигнал имеет ограниченный по ширине спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой, строго большей удвоенной верхней частоты.

Понятие о кодировании информации.

Код — это набор условных обозначений (или сигналов) для записи (или передачи) некоторых заранее определенных понятий.

Кодирование информации – это процесс формирования определенного представления информации. В более узком смысле под термином «кодирование» часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.

Обычно каждый образ при кодировании (иногда говорят — шифровке) представлении отдельным знаком.

Знак - это элемент конечного множества отличных друг от друга элементов.

Знак вместе с его смыслом называют символом.

Набор знаков, в котором определен их порядок, называется алфавитом. Существует множество алфавитов:

алфавит кириллических букв {А, Б, В, Г, Д, Е, ...}

алфавит латинских букв {А, В, С, D, Е, F,...}

алфавит десятичных цифр{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

алфавит знаков зодиака {картинки знаков зодиака} и др.

Особенно большое значение имеют наборы, состоящие всего из двух знаков: пара знаков {+, -}, пара цифр {0, 1}, пара ответов {да, нет}

Структурная схема канала передачи информации.

Рис. 1.3. Функциональная схема системы передачи дискретных

сообщений

Понятие о реальном и идеальном канале передачи информации.

Гауссовский канал и его разновидности.

ГАУССОВСКИЙ КАНАЛ

Основные допущения при построении такой модели следующие:

–коэффициент передачи и время задержки сигналов в канале не зависят от времени и являются детерминированными величинами, известными в месте приема сигналов;

–в канале действует аддитивная флуктуационная помеха – гауссовский "белый шум" (гауссовский процесс, характеризуется равномерной спектральной плотностью, нормально распределённым значением амплитуды и аддитивным способом воздействия на сигнал).

Гауссовский канал применяют как модель реальных каналов проводной связи и однолучевых каналов без замираний или с медленными замираниями. При этом замирания представляют собой неконтролируемые случайные изменения амплитуды сигнала. Такая модель позволяет анализировать амплитудные и фазовые искажения сигналов и влияние флуктуационной помехи.

ГАУССОВСКИЙ КАНАЛ С НЕОПРЕДЕЛЕННОЙ ФАЗОЙ СИГНАЛА

В этой модели время задержки сигнала в канале рассматривают как случайную величину, поэтому фаза выходного сигнала также случайна. Для анализа выходных сигналов канала необходимо знать закон распределения времени задержки или фазы сигнала.

ГАУССОВСКИЙ ОДНОЛУЧЕВОЙ КАНАЛ С ЗАМИРАНИЯМИ

В этой модели коэффициент передачи канала и фазовую характеристику канала рассматривают как случайные величины или процессы. В этом случае спектр выходного сигнала канала шире спектра входного даже при отсутствии помехи из-за паразитных амплитудной и фазовой модуляций. Такие модели достаточно хорошо описывают свойства радиоканалов различных диапазонов и проводных каналов со случайными, в том числе и переменными параметрами.

ГАУССОВСКИЙ МНОГОЛУЧЕВОЙ КАНАЛ С ЗАМИРАНИЯМИ

Эта модель описывает радиоканалы, распространение сигналов от передатчика к приемнику в которых происходит по различным "каналам" – путям. Длительность прохождения сигналов и коэффициенты передачи различных "каналов" являются неодинаковыми и случайными. Принимаемый сигнал образуется в результате интерференции сигналов, пришедших по разным путям. В общем случае частотная и фазовая характеристики канала зависят от времени и частоты.

ГАУССОВСКИЙ МНОГОЛУЧЕВОЙ КАНАЛ С ЗАМИРАНИЯМИ И АДДИТИВНЫМИ СОСРЕДОТОЧЕННЫМИ ПОМЕХАМИ

В этой модели наряду с флуктуационной помехой учитывают и различного вида сосредоточенные помехи. Она является наиболее общей и достаточно полно отражает свойства многих реальных каналов. Однако ее использование порождает сложность и трудоемкость задач анализа, а также необходимость сбора и обработки большого объема исходных статистических данных.

В настоящее время для решения задач анализа непрерывных и дискретных каналов используются, как правило, модель гауссовского канала и модель гауссовского однолучевого канала с замираниями.

1 2 3 4