10.1 Истечение газов. Основные понятия и математическое описание
Адиабатное истечение из суживающегося сопла. Сопло Лаваля
В настоящее время исключительно большое развитие получили различного рода лопаточные машины (паровые и газовые турбины, турбокомпрессоры и турбодетандеры), а также реактивные двигатели и т.д. Работа всех этих агрегатов связана с движением рабочего тела по каналам переменного сечения. В соответствии с существующей технической терминологией каналы, в которых движется рабочее тело (газ или пар), носят название сопел и диффузоров. Сопло - это канал, в котором потенциальная энергия потока превращается в кинетическую, т.е. канал, в котором скорость потока растет. Диффузор - канал, обеспечивающий торможение потока газа (или пара), сжатие рабочего тела, т.е. канал, в котором скорость потока уменьшается.
При рассмотрении первого закона термодинамики было установлено уравнение первого закона для потока газа
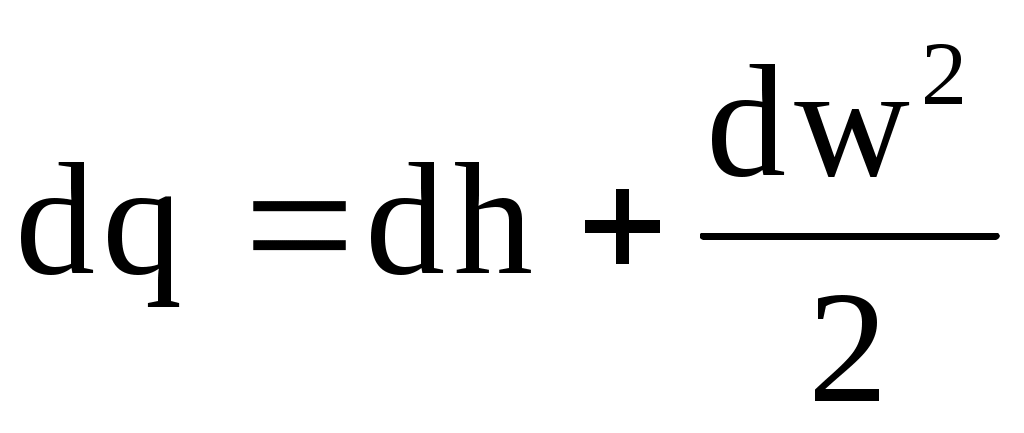 , (10.1) , (10.1)
где w - скорость движения рабочего тела.
В термодинамике принято считать течение рабочего тела по каналу адиабатным (dq = 0). Тогда уравнение (10.1) принимает вид dw2/2 = - dh, а поскольку dw2/2 = wdw, то получим
wdw = - dh. (10.2)
Для обратимого процесса истечения газа одновременно с уравнением (10.1) сохраняет силу уравнение (2.20) dq = dh - dp, которое при dq = 0 принимает вид
dh = dp. (10.3)
Тогда уравнение (10.2) с учетом (10.3) принимает вид
wdw - dp=0. (10.4)
Из уравнения (10.4) следует, что увеличение скорости движения сопровождается понижением давления газа и наоборот.
Уравнение (10.4) представим в следующем виде: разделим обе его части на w2, а числитель и знаменатель правой части умножим на произведение к р, где к - показатель адиабаты:
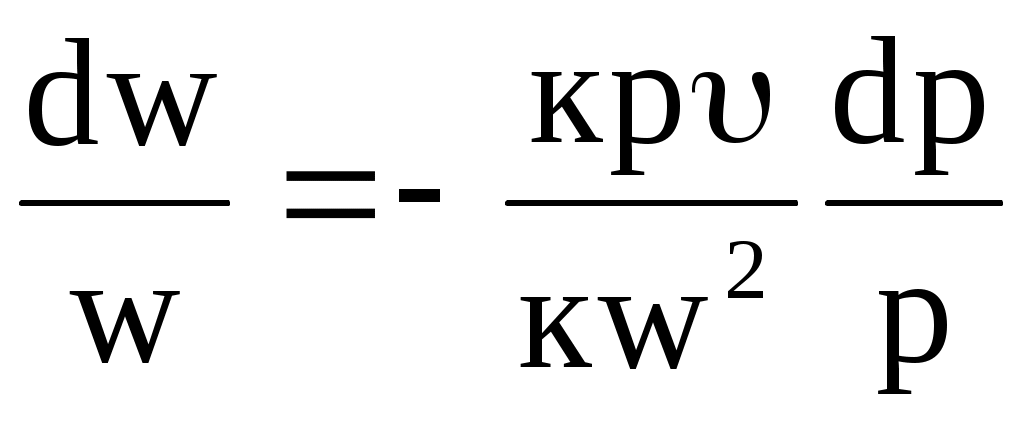 . (10.5) . (10.5)
Как известно из физики, местная скорость звука в газе, имеющем параметры p и :
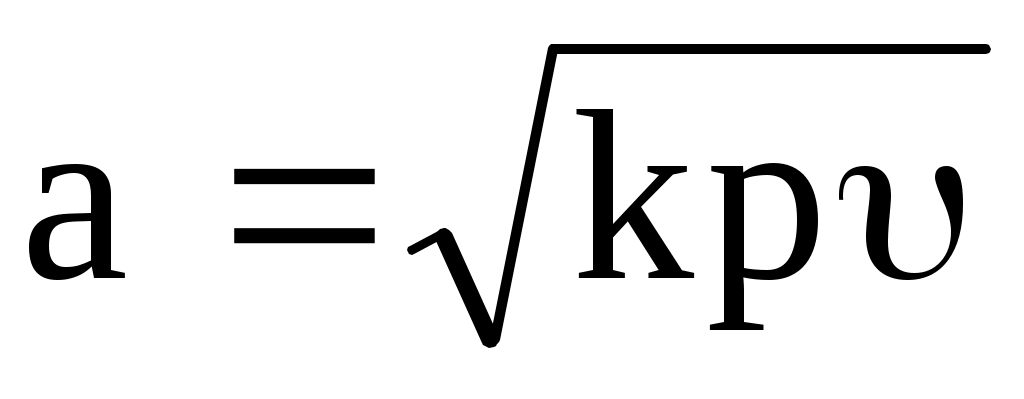 . (10.6) . (10.6)
При исследовании течений газа принято скорость движения относить к местной скорости звука; это отношение называют числом Маха (Ма).
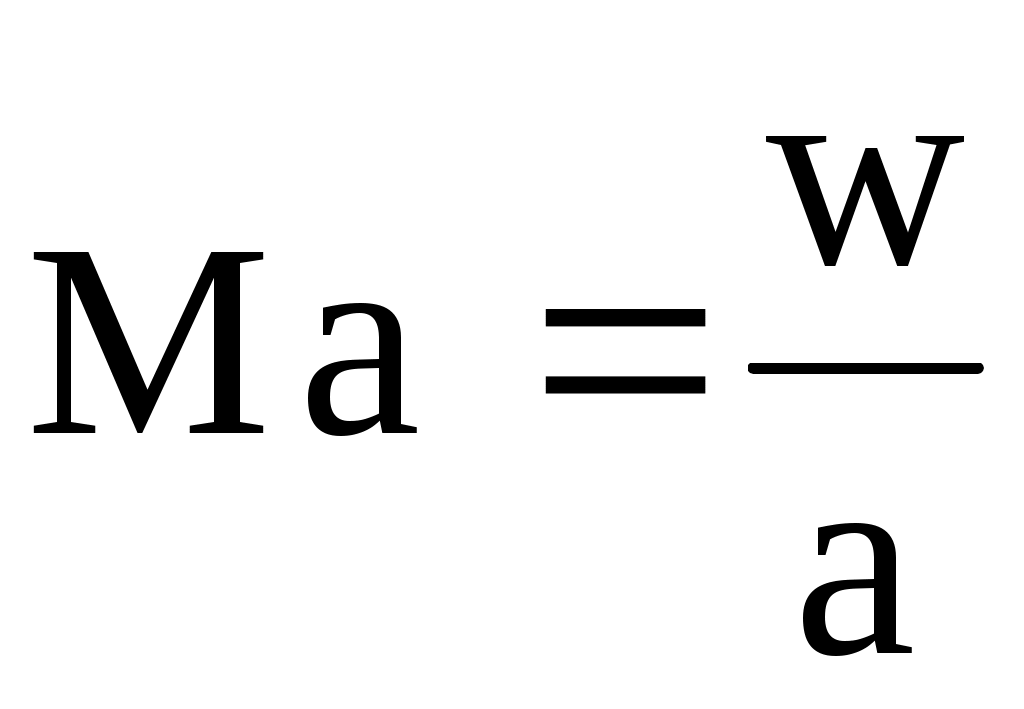 . (10.7) . (10.7)
Если Ма < 1, то скорость истечения называют дозвуковой, если Ма > 1 - сверхзвуковой.
С учетом (10.6) и (10.7) уравнение (10.5) запишется так:
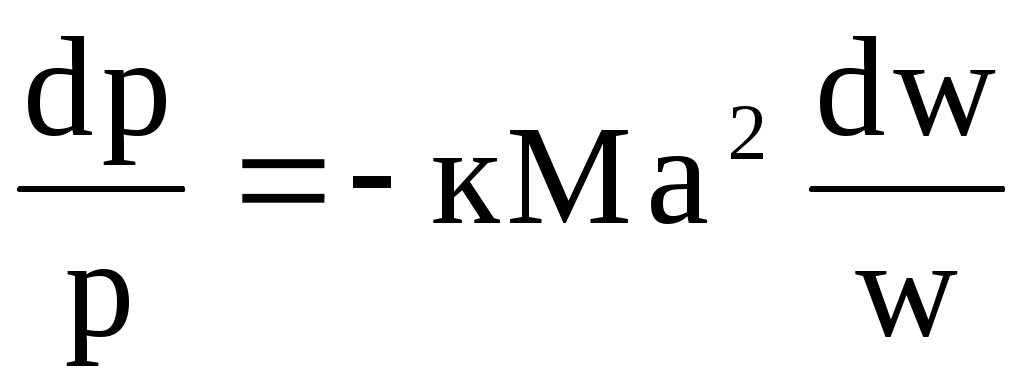 . (10.8) . (10.8)
Уравнение (10.8) называют уравнением Вулиса.
Пусть через поперечное сечение канала площадью f проходит газ со скоростью w. Удельный объем в этом сечении . При установившемся движении газа, когда не происходит разрыва струи, через каждое поперечное сечение канала в единицу времени протекает одинаковое массовое количество газа Y.
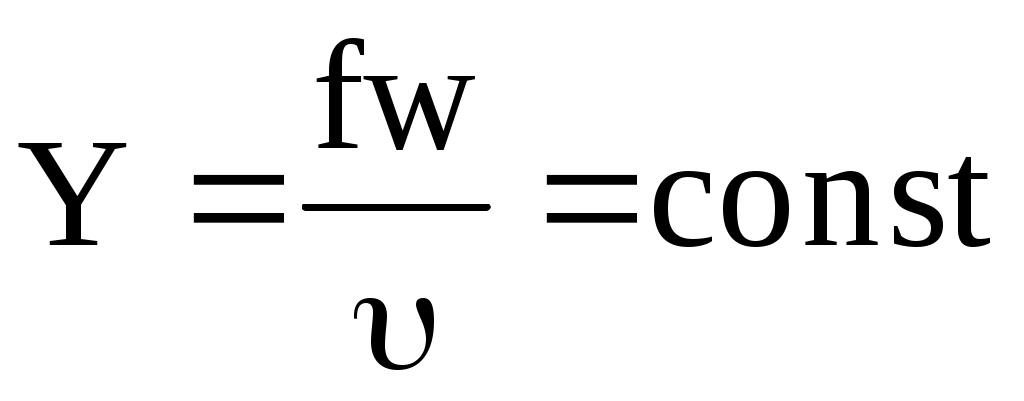 . (10.9) . (10.9)
Отсюда
Y = f w. (10.10)
Продифференцировав выражение (10.10) при Y= const, получим
Yd = fdw + wdf. (10.11)
Поделив (10.11) на выражение (10.10), получим уравнение сплошности
 . (10.12) . (10.12)
Прологарифмировав уравнение адиабаты pк = const, получим
кln + lnp = const. Продифференцировав последнее выражение, получим
кd/ + dp/p= 0. Отсюда
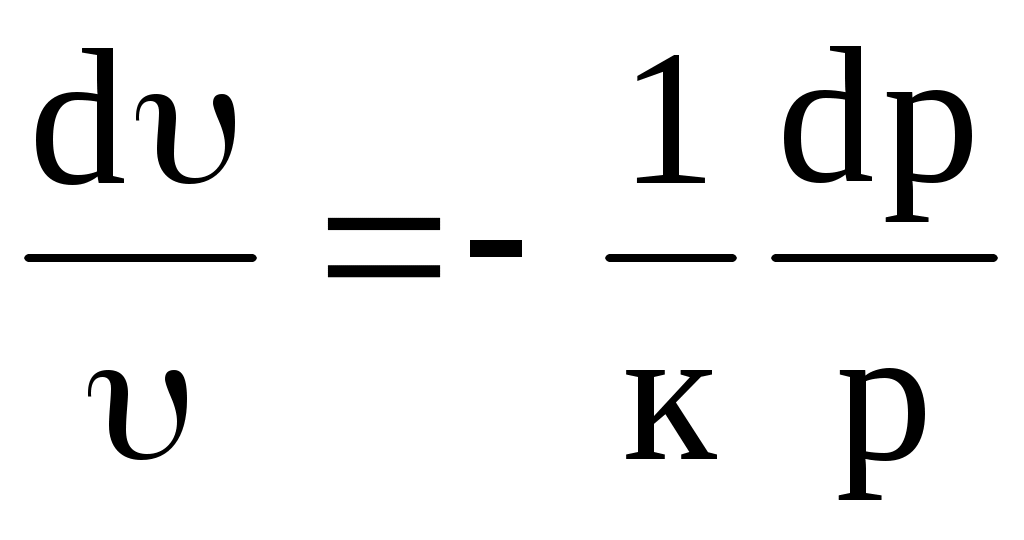 . (10.13) . (10.13)
Подставив (10.13) в уравнение (10.12) и умножив на - к, получим
 . (10.14) . (10.14)
Подставляя (10.14) в уравнение (10.8), получим
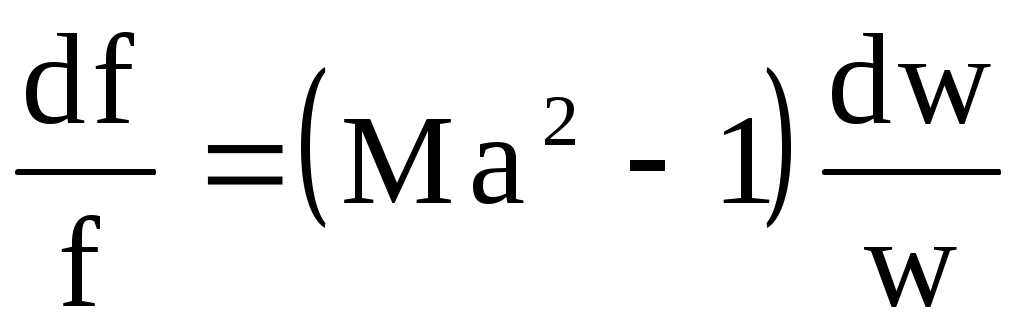 . (10.15) . (10.15)
Знак разности (Ма2 - 1) зависит от того, движется ли газ с дозвуковой или сверхзвуковой скоростью. При Ма = 1 газ имеет скорость равную местной скорости звука (w = а). В этом случае (Ма2 - 1) = 0. При движении со скоростью меньше скорости звука Ма < 1 (w < a) и (Ма2-1) < 0. При сверхзвуковой скорости Ма > 1(w > a) и (Ма2-1) > 0.
Анализ уравнения (10.15) позволяет выяснить профиль канала в зависимости от начальной скорости газа и знака изменения скорости.
Пусть ставится задача выяснить профиль сопла, т.е. нужно создать ускоренное движение газа (dw > 0) и вначале Ма < 1. На основании (10.15) должно быть df < 0, т.к. в правой части произведение положительной величины dw > 0 на отрицательную (Ма2-1) < 0 дает отрицательную величину, то есть профиль канала должен быть суживающимся (рис.10.1). По мере роста скорости w будет увеличиваться число Ма, когда Ма = 1 (w = a), правая часть (10.15) обратится в 0, т.е. df = 0. В этот момент сечение станет минимальным.
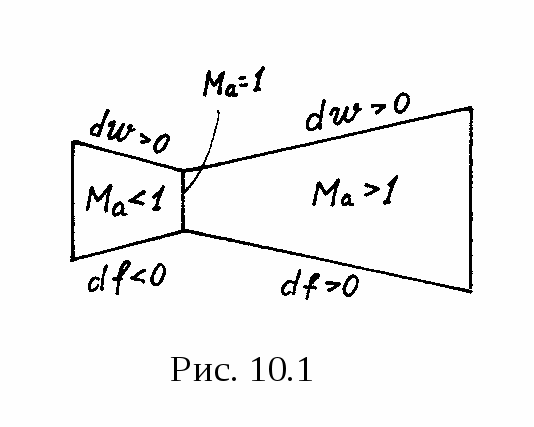
При Ма > 1 при ускоренном движении (dw>0) знак разности (Ма2-1) > 0, следовательно, должно быть df > 0 (рис. 10.1), т.е. канал должен быть расширяющимся.
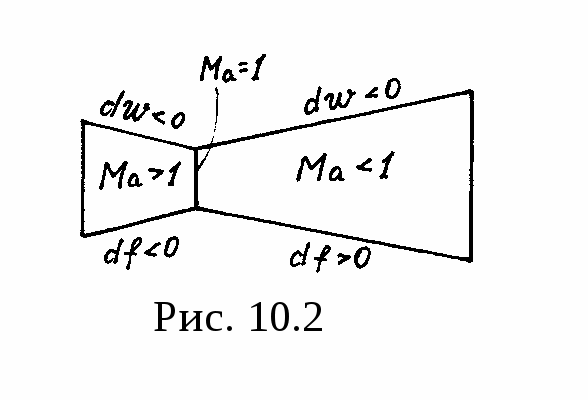
Пусть теперь ставится задача выяснить профиль диффузора, т.е. нужно создать замедленное движение (dw < 0). Если вначале газ движется со сверхзвуковой скоростью Ма > 1, то в правой части уравнения (10.15) получим отрицательный знак
(Ма2 - 1) 0 и dw < 0 и потому df < 0, т.е. сечение должно быть суживающимся (рис. 10.2). При Ма=1 df = 0. В дозвуковой области при Ма < 1 (Ма2 - 1) 0 получим df > 0, т.е. профиль канала должен быть расширяющимся (рис. 10.2).
Как видно, в обоих случаях при Ма = 1 df = 0 и поперечное сечение канала является минимальным. В нем скорость движения газа становится равной скорости звука и здесь происходит, как говорят, кризис течения газа, отсюда все величины, относящиеся к этому сечению: wкр, ркр, кр , называются критическими.
Таким образом, как сопла, так и диффузоры могут быть суживающимися и расширяющимися. В каждом отдельном случае профиль сопла или диффузора определяется величиной числа Ма.
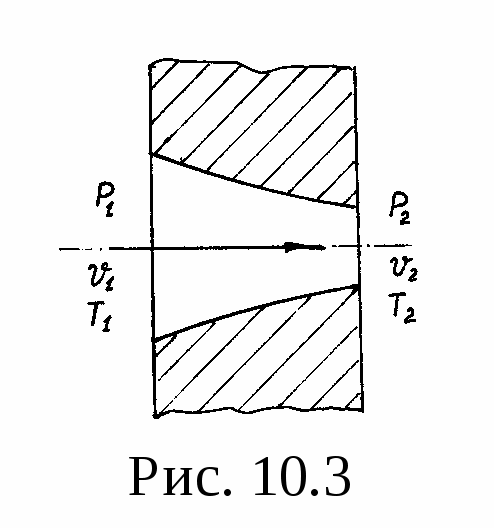
Адиабатное истечение из суживающегося сопла. Пусть в резервуаре, размеры которого достаточно большие, находится газ, вытекающий через суживающееся сопло. Обозначим параметры газа в резервуаре через p1, 1, Т1 (рис. 10.3). Значения этих параметров со временем не изменяются. В устье сопла устанавливается постоянное давление р2, которое будем считать равным давлению в среде, куда происходит истечение. Удельный объем и температуру в этой среде обозначим 2 и Т2. При движении по соплу газ переходит от параметров p1, 1, Т1 к параметрам p2, 2, Т2. При этом скорость его от одного сечения к другому увеличивается и достигает наибольшего значения в устье сопла. Если пренебречь теплообменом струи газа с внешней средой (за его малостью), то этот процесс можно считать адиабатным. Будем также считать его обратимым. Определим скорость истечения газа из сопла и его расход.
Интегрируя выражение (10.4) в пределах для w между w1 = 0 (ввиду малости w1 в сравнении с w2) и w2 = w и для давления между р1 и р2 получим
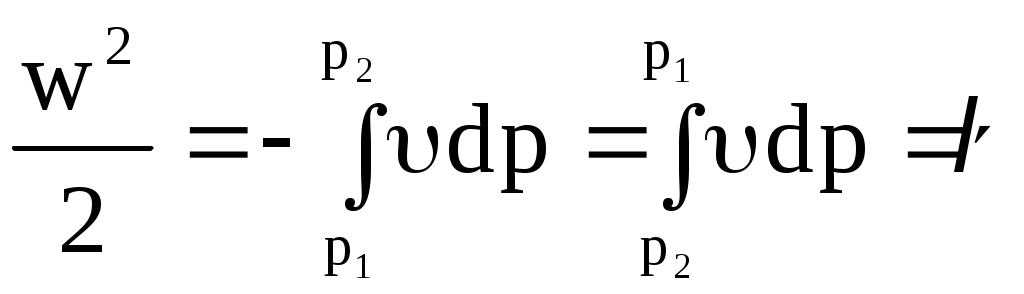 , (10.16) , (10.16)
где l - техническая работа при адиабатном расширении.
Подставив в (10.16) значение технической работы l по уравнению (4.26), получим выражение для скорости истечения
 . (10.17) . (10.17)
Скорость истечения w можно найти также из выражения (10.2). Интегрируя это уравнение в пределах от w1 = 0 до w2 = w и от h1 до h2, получим
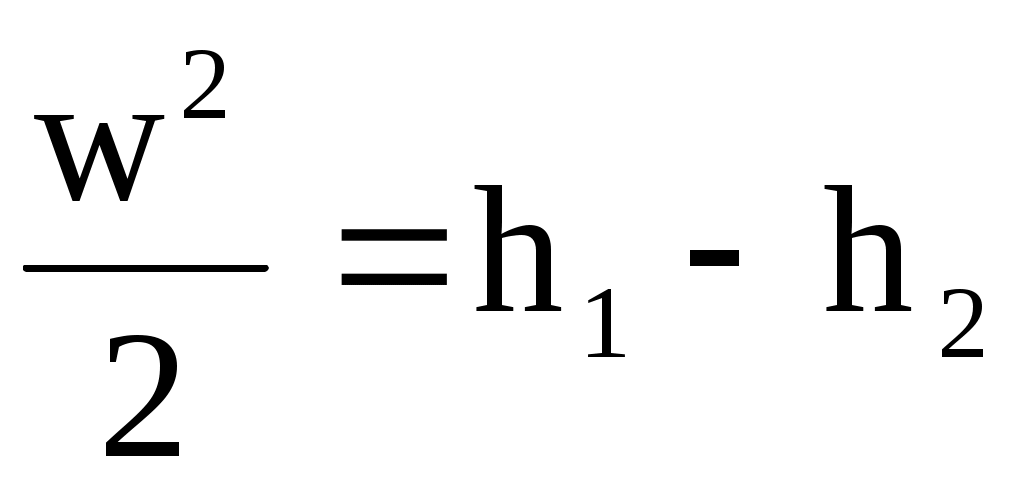 . (10.18) . (10.18)
Из уравнения (10.18) можно заключить, что кинетическая энергия газа, вытекающего из сопла, определяется разностью энтальпий начального и конечного состояний газа при его обратимом адиабатном расширении.
Из уравнения (10.18) имеем
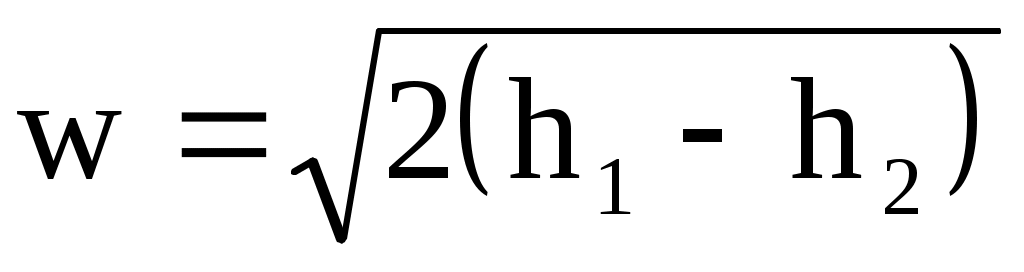 , (10.19) , (10.19)
где w в м/с, если h1 и h2 в Дж/кг.
Так как в таблицах энтальпия газа обычно приводится в кДж/кг, то формулу (10.19) записывают в виде
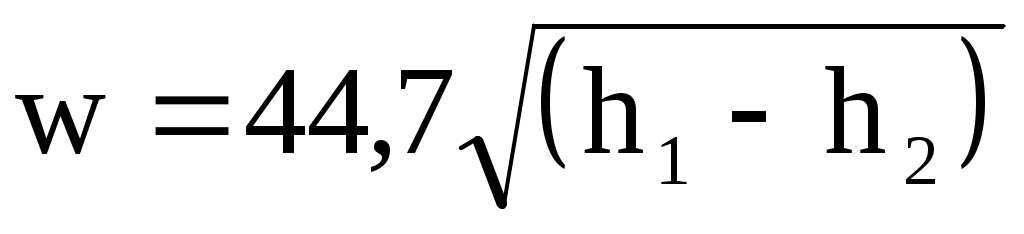 , (10.20) , (10.20)
где h1 и h2 в кДж/кг, a w в м/с.
Массовый расход газа через сопло найдем по выражению (10.9), которое запишем в следующем виде: 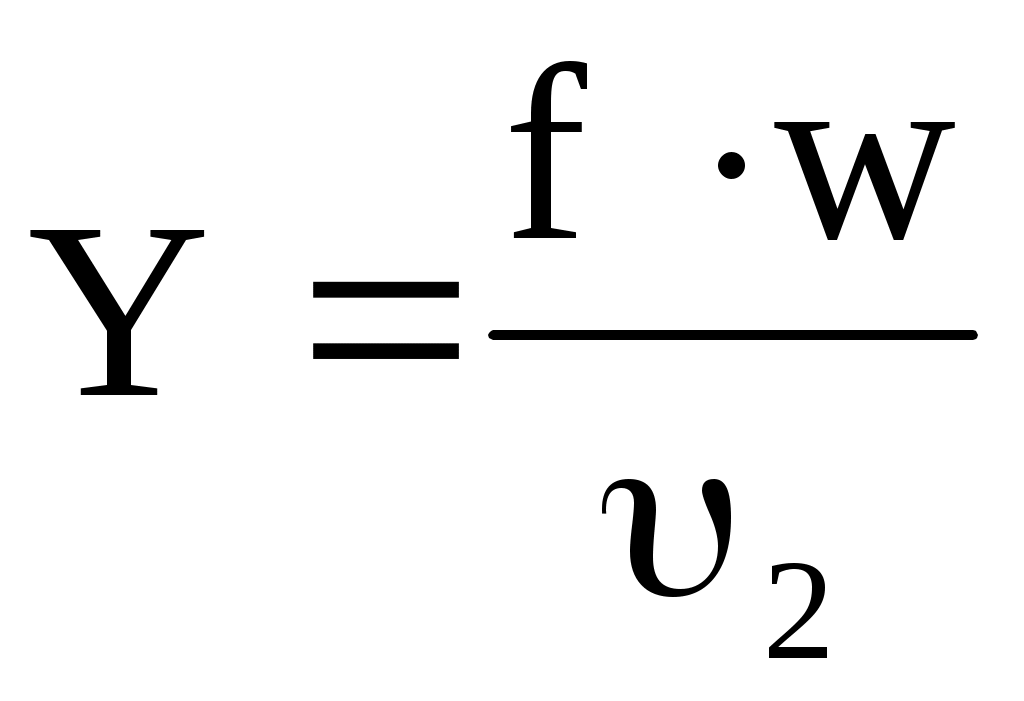 , (10.21) , (10.21)
где f - площадь выходного сечения (устья) сопла; 2 - удельный объем газа в выходном сечении.
Из связи параметров в адиабатном процессе имеем
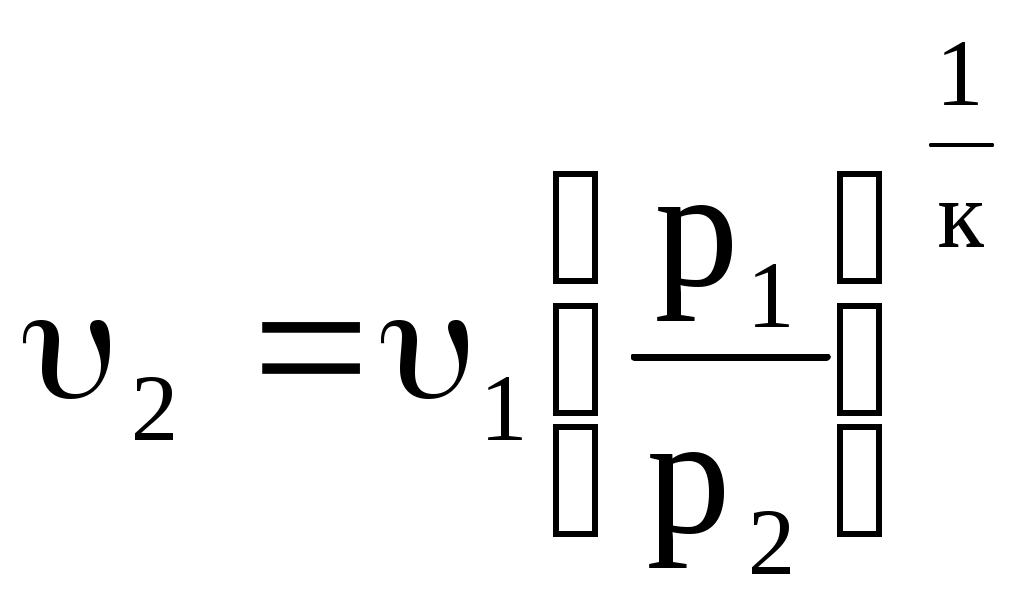 или или 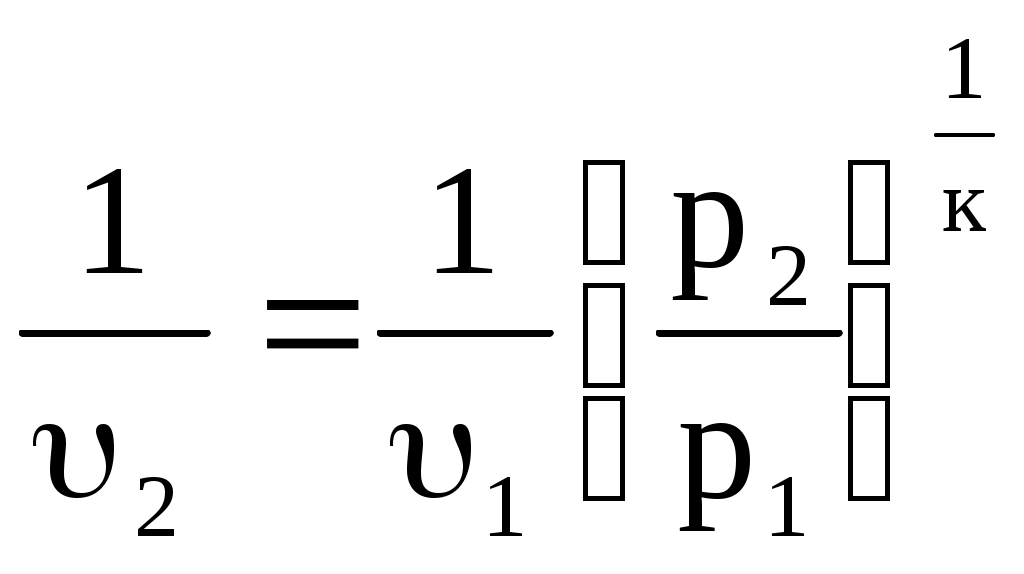 . (10.22) . (10.22)
Подставляя (10.17) и (10.22) в уравнение (10.21) получим
 . (10.23) . (10.23)
Обозначая = р2/р1 и подставляя в (10.17) и (10.23), запишем выражения для скорости и массового расхода
 . (10.24) . (10.24)
 . (10.25) . (10.25)
Критическая скорость и максимальный расход газа. Рассмотрим, как изменяется расход Y газа через сопло, если начальное давление р1 остается постоянным, а давление среды р2 принимает различные значения. Построим диаграмму этого изменения в координатах Y - (рис. 10.4). Пусть р2 = р1, т.е. = 1, тогда из уравнения (10.25) следует, что Y = 0. Т.е. в том случае, когда давление в среде, куда должно происходить истечение, равно давлению входа в сопло, никакого истечения не происходит, что вполне понятно. Допустим р2 = 0, т.е.
= 0, тогда из (10.25) следует, что Y = 0. Т.е. получается, что при истечении в среду, где имеется полный вакуум, расход газа будет равен нулю. Что совсем непонятно.
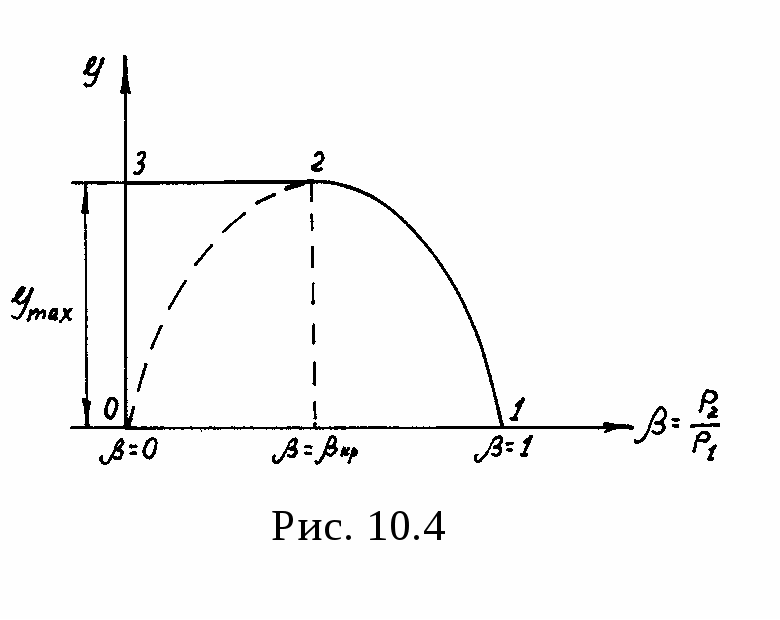
При подстановке в уравнение (10.25) промежуточных значений между 0 и 1 получим кривую 1-2-0 (рис.10.4). Как показано на рисунке, при уменьшении р2, а следовательно, и , расход газа сначала увеличивается и при 0,5 достигает максимума, после чего начинает падать и при = 0 становится равным 0.
Опыт показывает, что расход газа в правой половине диаграммы совпадает с получаемым по уравнению (10.25), т.е. поднимаемся по кривой 1-2, при дальнейшем понижении р2 (а следовательно, и ) расход газа остается постоянным и максимальным, т.е. идет по линии 2-3. Максимальному расходу соответствует в устье сопла критическое давление, при котором скорость истечения
w = а (Ма = 1). При этом ркр/р1 = кр.
Характер реальной кривой расхода 1-2-3 (рис.10.4) объясняется следующим. При давлении среды р2 ркр давление в устье сопла руст = р2. Когда давление среды р2 понизится до ркр, давление в устье руст = ркр. При дальнейшем понижении давления среды р2 ркр давление в устье сопла остается постоянным, равным руст = ркр. Формулу (10.25) можно считать правильной и для левой половины рис. 10.4, если понимать в ней под р2 не давление окружающей среды, а давление в устье сопла. Невозможность, начиная с определенного момента, дальнейшего понижения давления в устье суживающегося сопла объясняется характером распространения изменения давления в газовой среде. Всякое изменение давления, произведенное в какой-либо точке неподвижной газовой среды, распространяется со скоростью звука в данной среде.
Рассмотрим с этой точки зрения явление истечения газа. Так как распространение изменения давления происходит в движущейся среде, т.е. в вытекающей из сопла струе газа, надо различать абсолютную скорость распространения волны пониженного давления и относительную скорость. Если в среде, куда происходит истечение газа, понизить давление до некоторого значения р2, то волна пониженного давления в вытекающей струе будет распространяться с абсолютной скоростью, равной скорости звука а. Относительная скорость волны пониженного давления, относительно неподвижного сопла, будет равна разности скоростей звука и движения струи: а - w (рис.10.5). При уменьшении р2 и эта разность будет становиться все меньше, т.к. w будет увеличиваться. Наконец наступит момент, когда а - w = 0. В этом случае в устье сопла установится скорость w = wкр = а. А давление р2 в этом случае будет равно ркр, которое устанавливается в устье сопла.
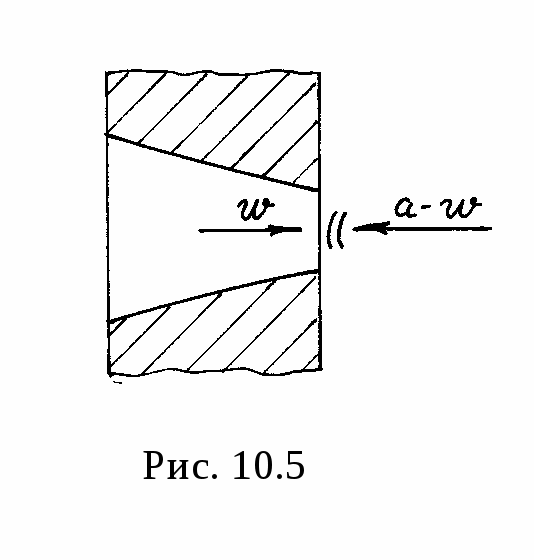
Если понижать давление в среде р2 дальше, ниже критического, то распространяясь в среде со скоростью звука, волна пониженного давления подойти к устью сопла не сможет, т.к. в последнем будет газ, вытекающий также со скоростью звука. Выходящая из сопла струя, попадая в среду с меньшим давлением, будет расширяться уже в самой среде. Таким образом, в суживающемся сопле нельзя получить скорость больше скорости звука.
Найдем максимальный расход Ymax и соответствующую ему критическую скорость wкр. Значение кр, при котором устанавливается максимальный секундный расход и критическая скорость (в соответствии с правилами отыскания экстремума), может быть получено, если взять в формуле (10.25) первую роизводную от выражения в скобках и приравнять ее нулю,
то есть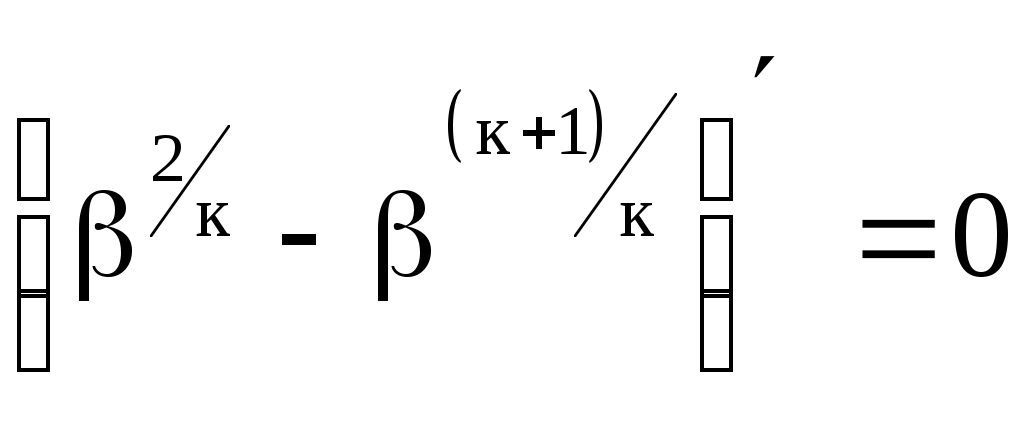 . .
Продифференцировав, получим 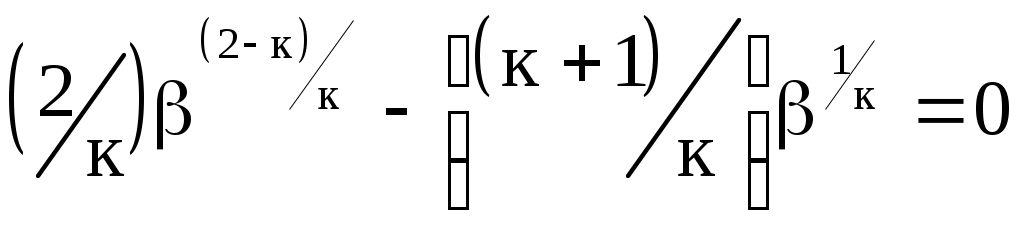 . Поделив последнее выражение на (2-к)/к и производя некоторые преобразования, получим . Поделив последнее выражение на (2-к)/к и производя некоторые преобразования, получим
 . (10.26) . (10.26)
Из выражения (10.26) видно, что кр целиком определяется значением показателя адиабаты к , т.е. физическими свойствами вытекающего газа. Так, при к = 1,4 кр = 0,528.
Подставив в выражения (10.24) и (10.25) значение кр по (10.26), получим формулы для определения wкр и Ymax.
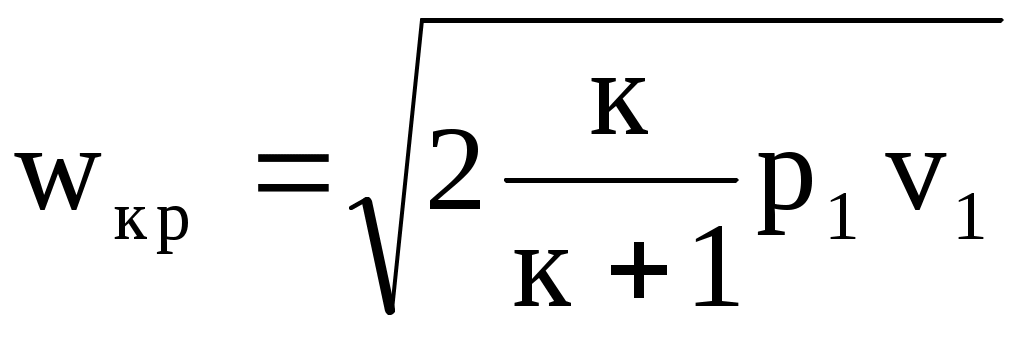 ; (10.27) ; (10.27)
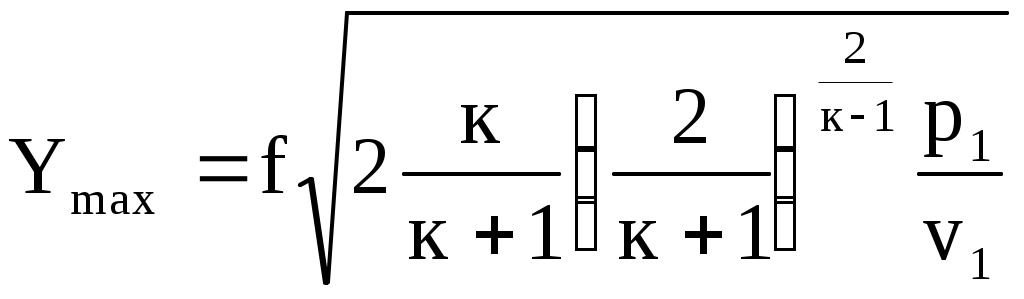 . (10.28) . (10.28)
Для скорости wкр можно также записать, согласно уравнению (10.20):
 . (10.29) . (10.29)
Таким образом, при истечении газа из суживающегося сопла следует различать три случая:
1) 1 > > кр. В этом случае скорость истечения и расход зависят от отношения р2/р1 и определяются по формулам (10.17) и (10.23). Здесь весь перепад давления от р1 до р2 используется на увеличение кинетической энергии газа;
2) = кр. В этих условиях секундный расход достигает максимального значения. Давление р2 = ркр, а скорость w = wкр. Скорость и расход определяются по формулам (10.27) и (10.28);
3) кр > > 0. В этом случае, Y достигнув своего максимального значения при = кр, дальше не увеличивается, скорость также остается постоянной, равной wкр. Yи w здесь, как и в предыдущем случае, определяются по формулам (10.28) и (10.27), то есть в этом случае для увеличения кинетической энергии газа используется не весь перепад давлений - от р1 до р2, а только часть его - от р1 до ркр.
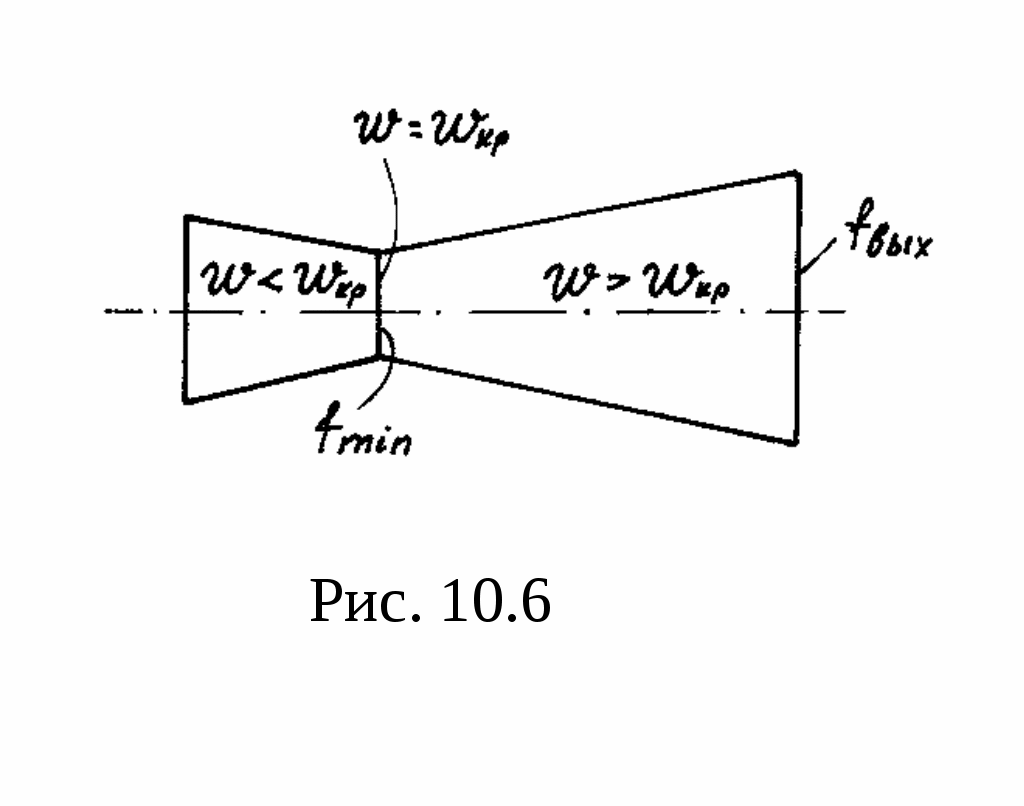
Если в среде, куда происходит истечение, давление ниже критического, то понизить давление на выходе из сопла до этого давления можно, как это было показано ранее, присоединением к суживающемуся соплу расширяющейся части, в которой и происходит требующееся для увеличения скорости падение давления ниже критического. Такое сопло впервые предложил шведский инженер Лаваль. Оно имеет вид, изображенный на рис. 10.6, и носит его имя (сопло Лаваля). Скорость на выходе из сопла Лаваля определяется по формуле (10.17), а расход по формуле (10.23), в которой под f надо понимать fвых, т.е
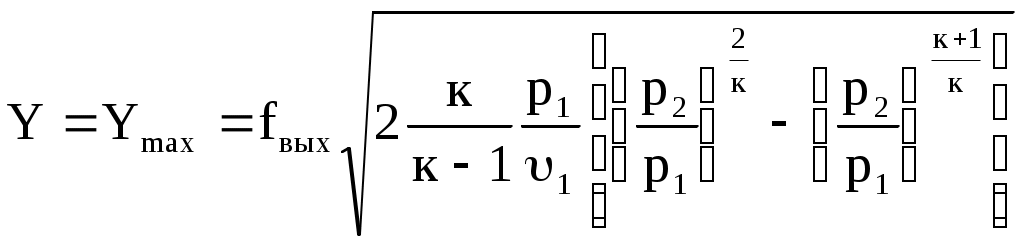 (10.30) (10.30)
С другой стороны, расход может быть подсчитан по формуле (10.28),
где f = fmin,
т.е. . (10.31) . (10.31)
Несмотря на то, что w > wкр, расход газа остается постоянным, равным Ymax.
Обычно расчет сопла Лаваля проводится по заданному расходу газа Y и параметрам р1 и 1 на входе, задается также давление среды р2. Тогда из формул (10.30) и (10.31) можно подсчитать
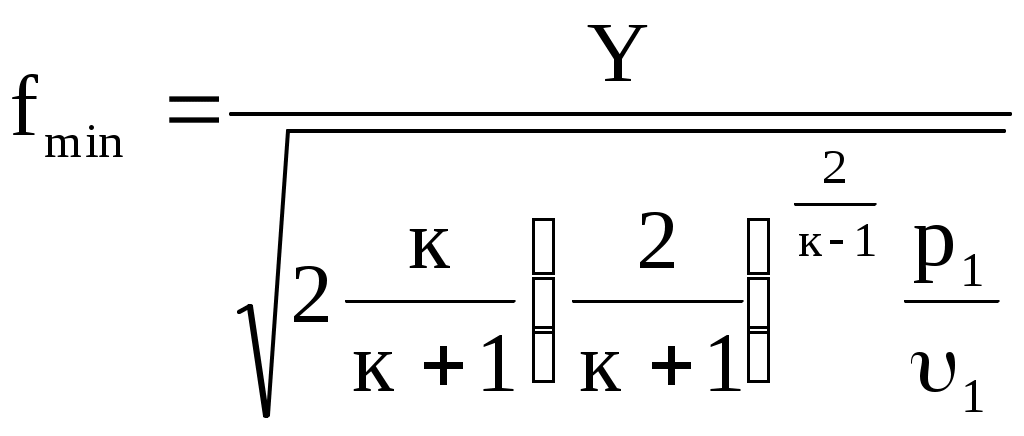 ; (10.32) ; (10.32)
и 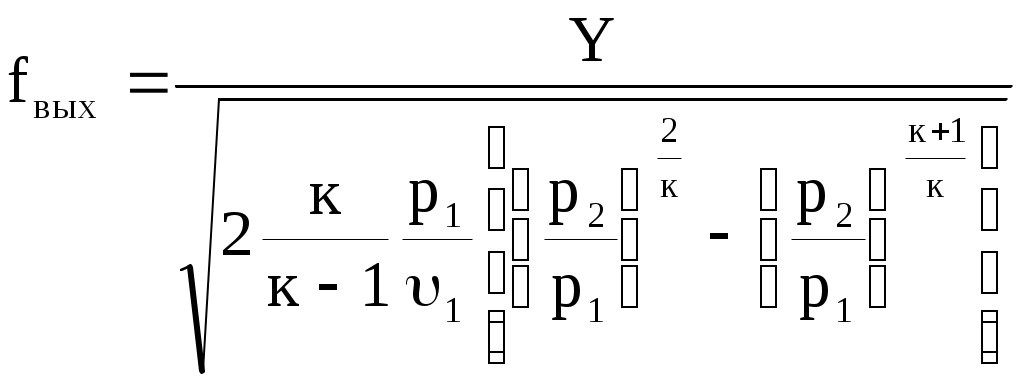 . (10.33) . (10.33)
Если взять отношение fвых/fmin, то получим
 . (10.34) . (10.34)
Задаваясь различными значениями давления р2 по формуле (10.34), можно вычислить соответствующую этому давлению площадь поперечного сечения сопла, то есть эта формула позволяет решить вопрос о профилировании сопла. Если допустить, что расширяющаяся часть сопла Лаваля выполнена с прямолинейными образующими и углом конусности , то длина этой части сопла (рис. 10.7) найдется по формуле
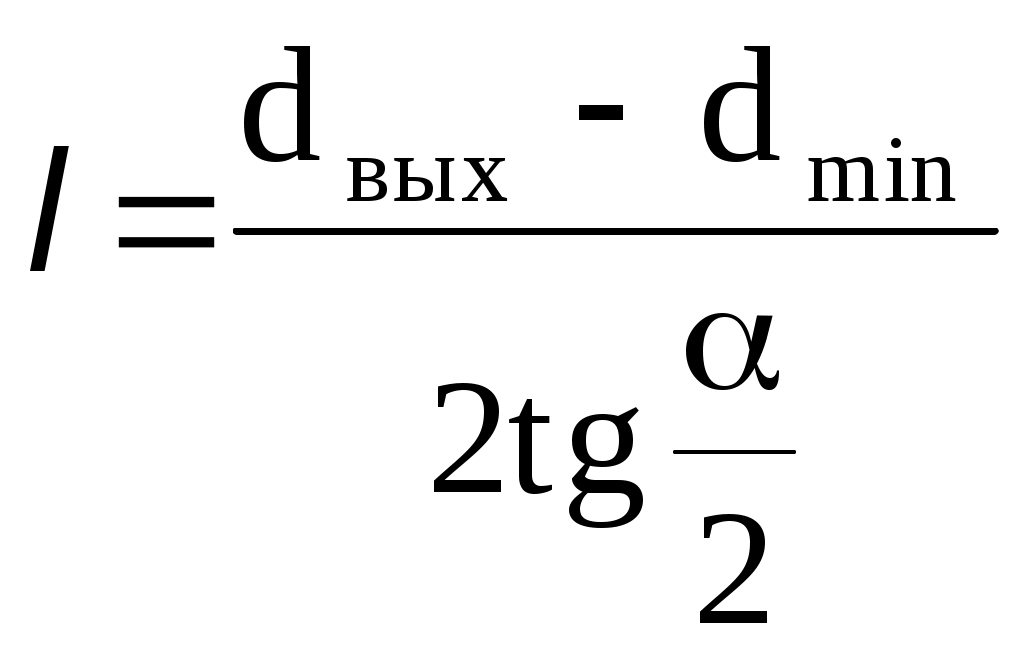 . .
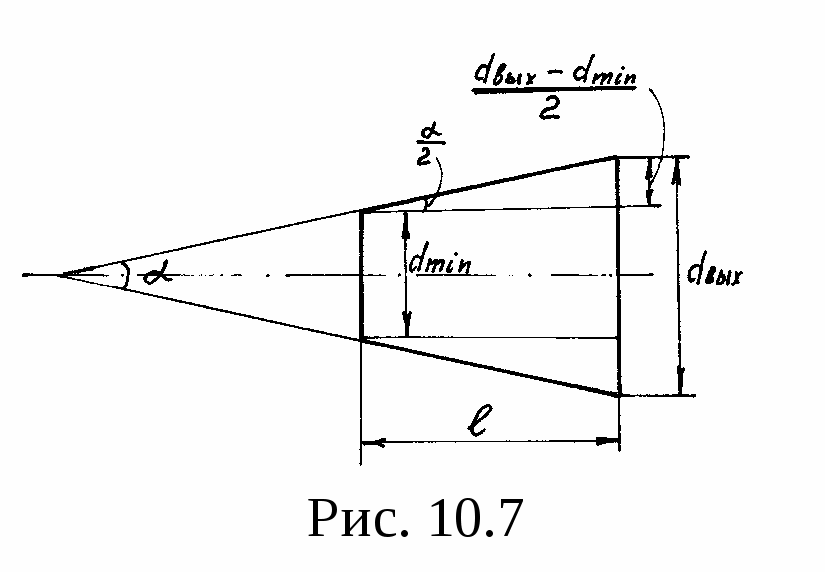
Однако следует помнить, что в сопле Лаваля можно получить w > wкр лишь в том случае, если р2/р1 < кр. Если же р2/р1 > кр, то в fmin сопла w < wкр, а расширяющаяся часть ведет себя как диффузор. Комбинированное сопло начинает работать как диффузор и в том случае, если скорость газа на входе в сопло больше скорости звука.
10.2 Истечение пара. Истечение с учетом трения
Основные положения и формулы теории истечения газа, установленные выше, в полной мере относятся к процессам истечения пара. Вопрос усложняется лишь тем, что пар при адиабатном расширении может изменить свое агрегатное состояние и перейти из перегретого состояния в насыщенное. В связи с этим усложняется выбор показателя адиабаты к , входящего в основные расчетные формулы. Это заставляет во всех случаях, когда это возможно, производить расчет процесса истечения пара с применением h, s-диаграммы и с использованием формулы (10.20).
При расчете истечения пара через суживающееся сопло, как и в случае истечения газа, возможны три случая.

1) 1 > > кр. Происходит полное расширение пара от р1 до р2. Скорость w < wкр и определяется по формуле  . Массовый секундный расход пара найдется по формуле . Массовый секундный расход пара найдется по формуле
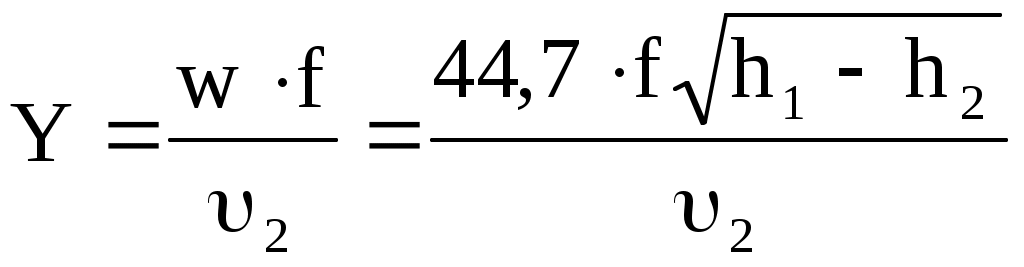 , ,
где f - выходное сечение сопла, h1, h2 и 2 снимаются с диаграммы h, s (рис. 10.8);
= кр. В этом случае происходит также полное расширение пара от р1 до р2 = ркр.
Скорость истечения пара равна wкр, а расход - Ymax.
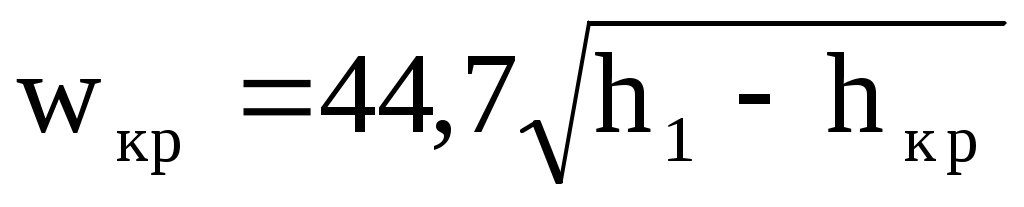 , ,
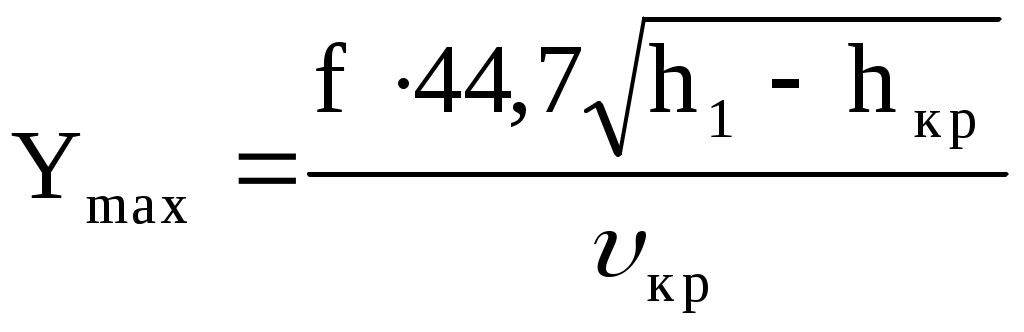 , ,
где h1, hкр и кр снимаются с диаграммы h, s (рис. 10.9);
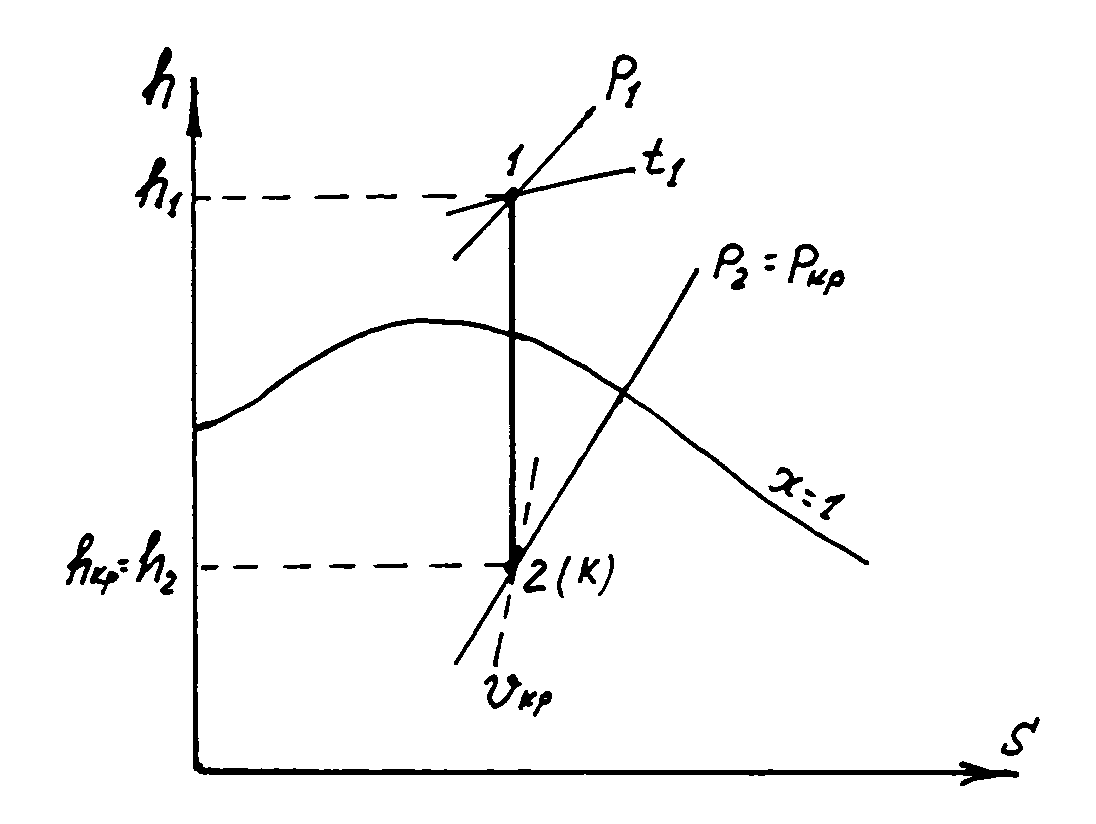
Рис. 10.9
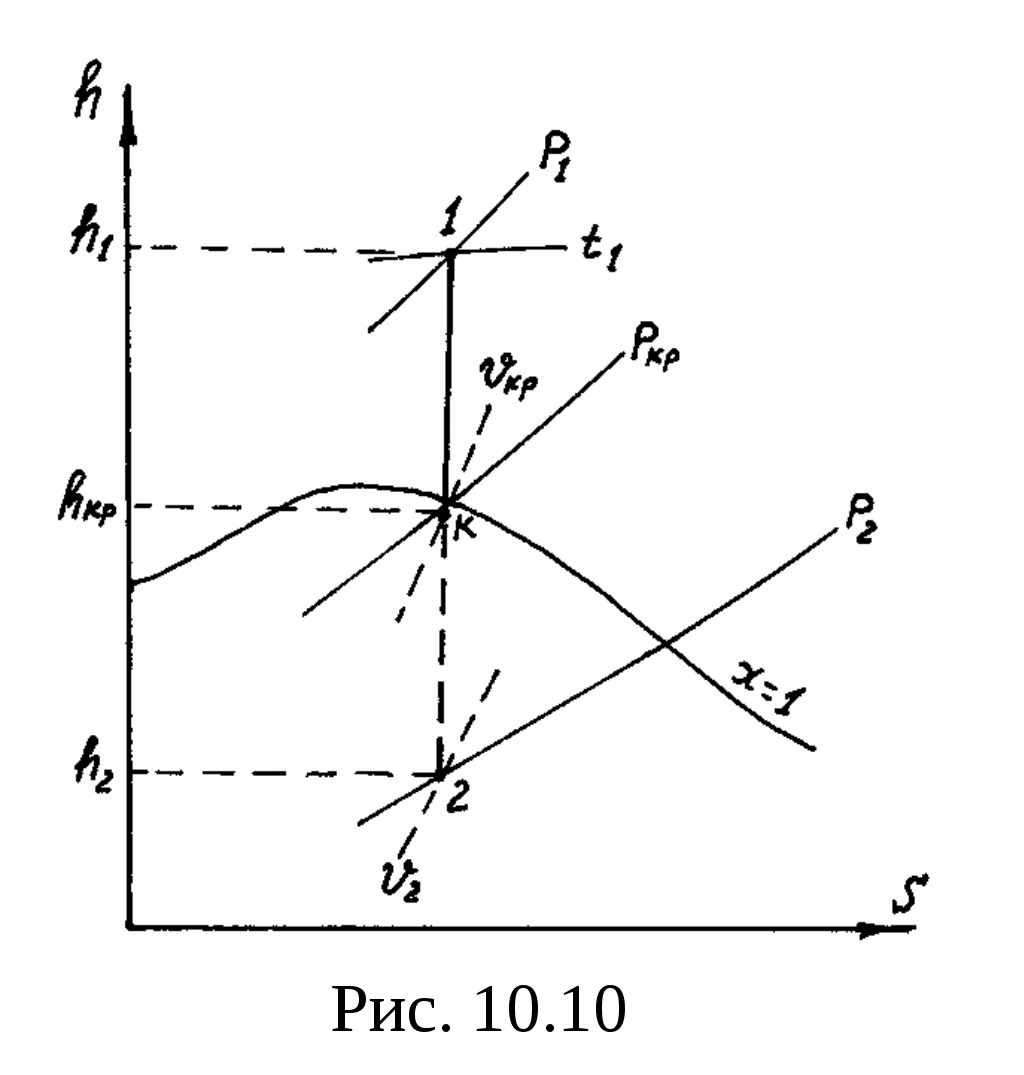
3) кр > > 0. В этом случае пар в пределах сопла расширяется от р1 до ркр, а расширение от ркр до р2 происходит за пределами сопла (рис. 10.10). Расчет wкр и Ymax по тем же формулам, что и в предыдущем случае.
При расчете истечения пара через сопло Лаваля можно также воспользоваться рис. 10.10. Только в этом случае расширение от р1 до ркр происходит в суживающейся части сопла, а расширение от ркр до р2 - в расширяющейся части сопла Лаваля. Скорость в минимальном сечении сопла 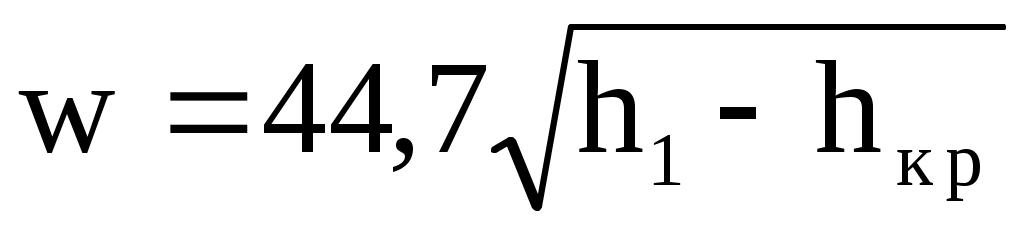 , а скорость на выходе из сопла Лаваля , а скорость на выходе из сопла Лаваля 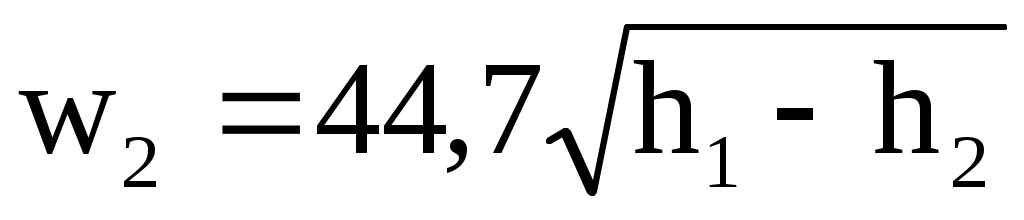 . Максимальный расход по одной из формул Ymax=wкрfmin/кр или Ymax=w2fвых/2. Из этих формул можно найти fmin и fвых. . Максимальный расход по одной из формул Ymax=wкрfmin/кр или Ymax=w2fвых/2. Из этих формул можно найти fmin и fвых.
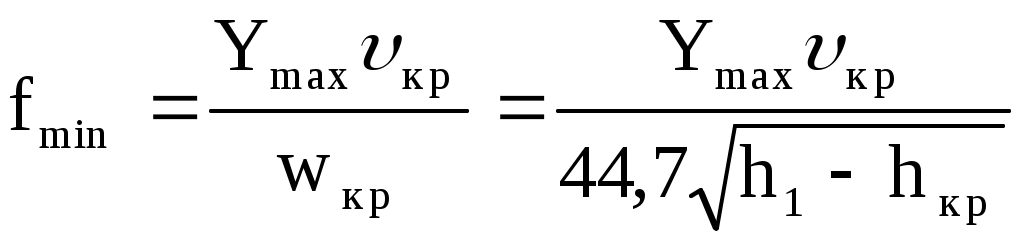 , , 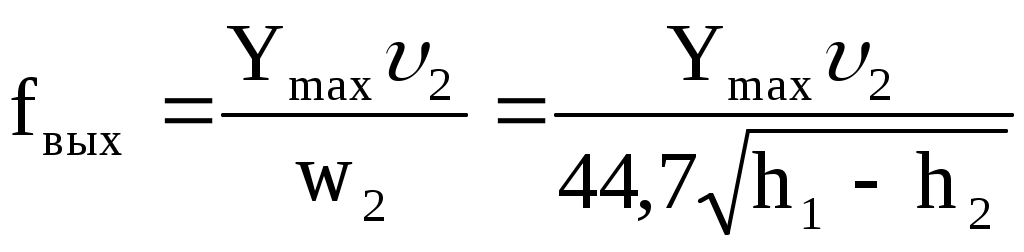 . .
Выведенные выше формулы скорости и секундного расхода газа и пара справедливы для обратимого процесса истечения, т.е. не учитывают силы трения рабочего тела о стенки канала и внутреннее трение.
Отношение действительной скорости истечения wq к теоретической w называют коэффициентом скорости или скоростным коэффициентом сопла = wq/w. Тогда wq = w. Для сопел современных турбин
= 0,93 - 0,98.
Потеря кинетической энергии при течении с трением
 , ,
где = (1 - 2) - коэффициент потери энергии в сопле.
Отношение действительной кинетической энергии рабочего тела wq2/2 к теоретической w2/2 называют к.п.д. сопла.
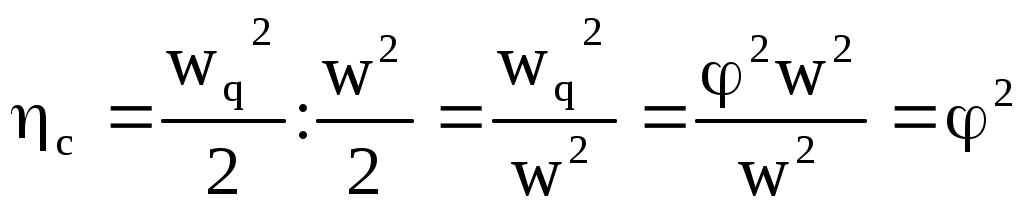 . .
Следовательно, к.п.д. сопла с равно квадрату скоростного коэффициента сопла.
10.3. Дросселирование газов и паров
Если на пути движения газа (или пара) по трубопроводу имеется местное сужение (например, прикрытый вентиль, задвижка, клапан, диафрагма и т.д.), то при прохождении газа через это сужение происходит уменьшение его давления. Такой процесс, в котором газ расширяется без совершения работы, называется дросселированием или мятием. Явление дросселирования в технике распространено довольно широко. Каждый вентиль, задвижка и т.д., уменьшающие проходное сечение трубопровода, вызывают дросселирование, возникающее при этом, как неизбежный процесс. Во многих же случаях дросселирование вводится как необходимый процесс, осуществляемый для определенных целей. Так, например, дросселированием пара в некоторых паровых турбинах осуществляется изменение их мощности. Широко используется дросселирование в холодильной и криогенной технике.
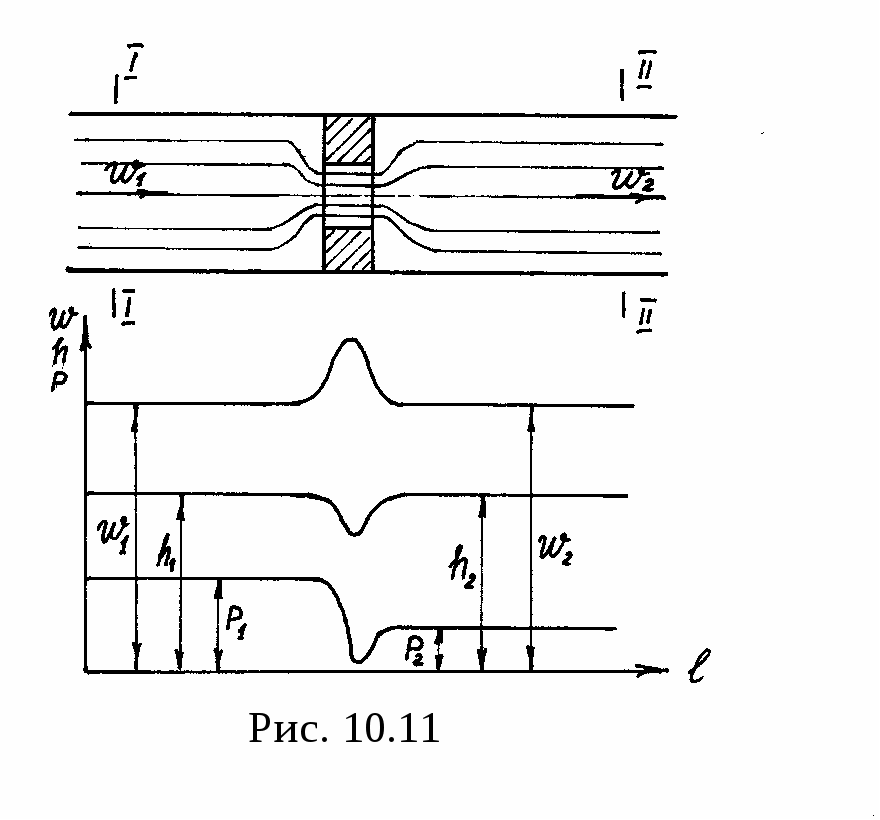
В процессе дросселирования происходит следующее изменение состояния газа. При прохождении газа через суженное сечение (рис. 10.11) увеличивается его скорость и уменьшается давление. За суженным сечением происходит обратное явление: скорость газа уменьшается, а давление увеличивается, но до начального давления р1 оно не поднимается. При этом часть кинетической энергии вследствие трения в суженной части превращается в теплоту, которая воспринимается газом. Вследствие неразрывности потока можно скорости w1 и w2 на некотором удалении от сужения (в сечениях I-I и II-II) считать равными. Тогда можно предположить, что должны выровняться и давления, однако в действительности оказывается р1 > р2, следовательно, между сечениями I-I и
II-II протекает необратимый процесс.
Для выявления изменения энтальпии воспользуемся уравнением первого закона термодинамики для потока газа dq = dh + dw2/2. Если считать, что процесс дросселирования протекает адиабатно (вследствие его краткости), то получим dh + dw2/2 = 0. Проинтегрировав это уравнение, получим
(w22 - w12)/2 = h1 - h2, а т.к. w1 = w2, то получим
h1 = h2 . (10.35)
Таким образом, с достаточной для технических расчетов точностью можно считать, что при дросселировании энтальпия остается постоянной. Однако следует отметить, что соотношение (10.35) отмечает лишь конечный результат процесса, отнесенный к сечениям I-I и II-II, достаточно удаленным от сужения. В самом же сужении энтальпия сначала уменьшается, а потом возрастает до первоначальной величины (рис. 10.11).
Эффект Джоуля-Томсона. Опытами установлено, что в результате дросселирования изменяется температура рабочего тела. Это явление названо эффектом Джоуля-Томсона. Рассмотрим, как изменяется температура при дросселировании идеального и реального газа. Энтальпия идеального газа есть однозначная функция температуры: dh = cpdT. На основании (10.35) dh = 0, следовательно, и dT=0, т.е. получим Т1 = Т2. Таким образом, при дросселировании идеального газа его температура остается постоянной.
Для установления изменения температуры в реальном газе рассмотрим эффект при изменении давления на бесконечно малую величину. Температурный эффект при бесконечно малом изменении давления называют дифференциальным дроссель-эффектом и обозначают = dT/dp. Дифференциальный дроссель-эффект может быть определен по уравнению (6.19) из раздела дифференциальных уравнений термодинамики
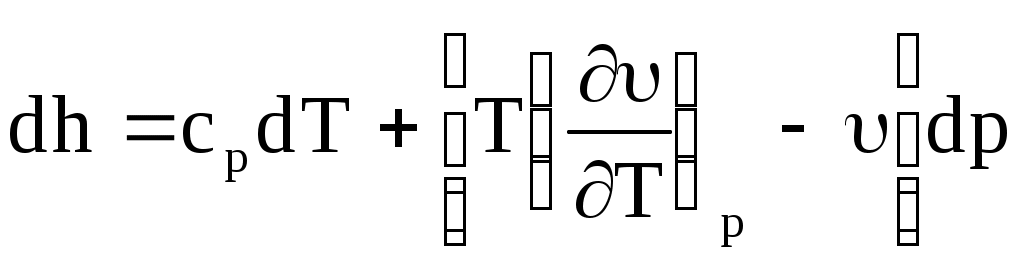 . .
Из этого уравнения при dh = 0 получим 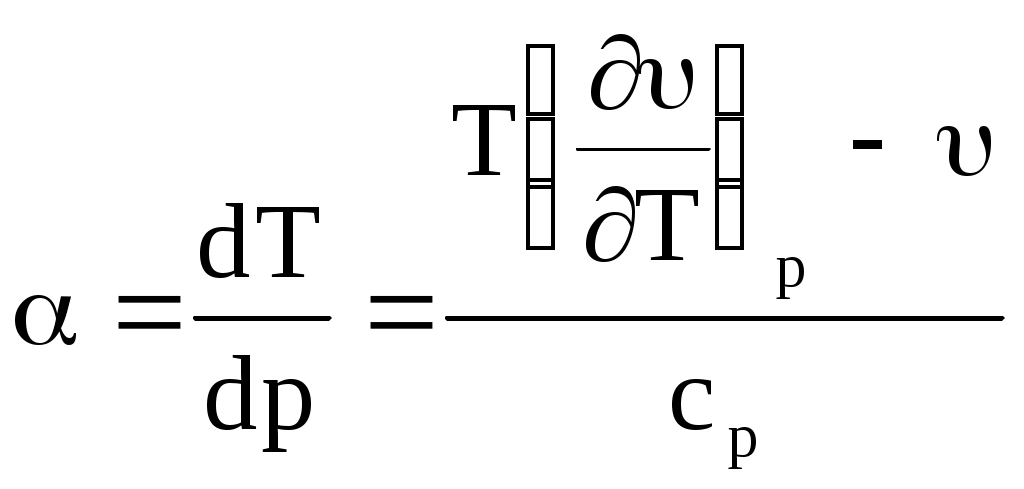 (10.36) (10.36)
или 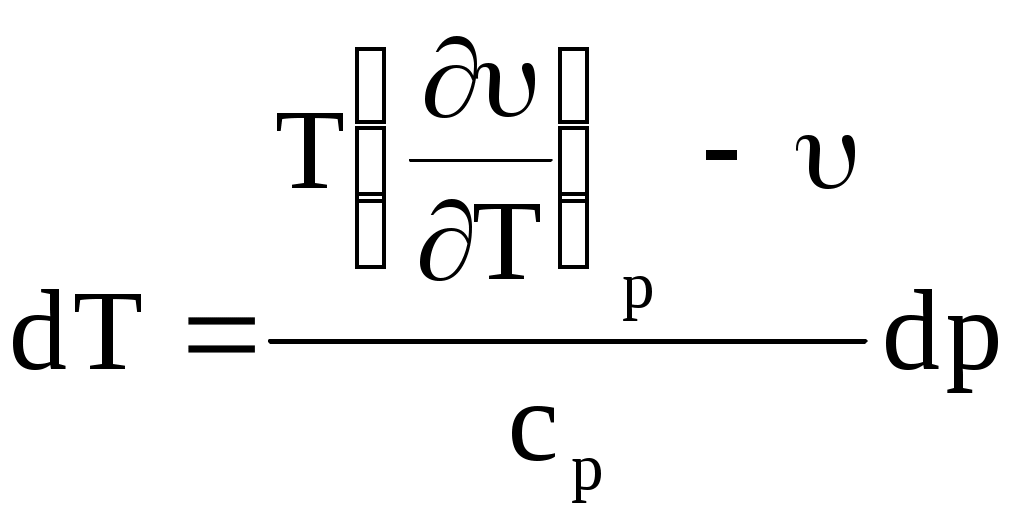 . (10.37) . (10.37)
Температурный эффект при конечном изменении давления газа при дросселировании называют интегральным дроссель-эффектом. Тогда соответствующая разность температур найдется при интегрировании выражения (10.37):
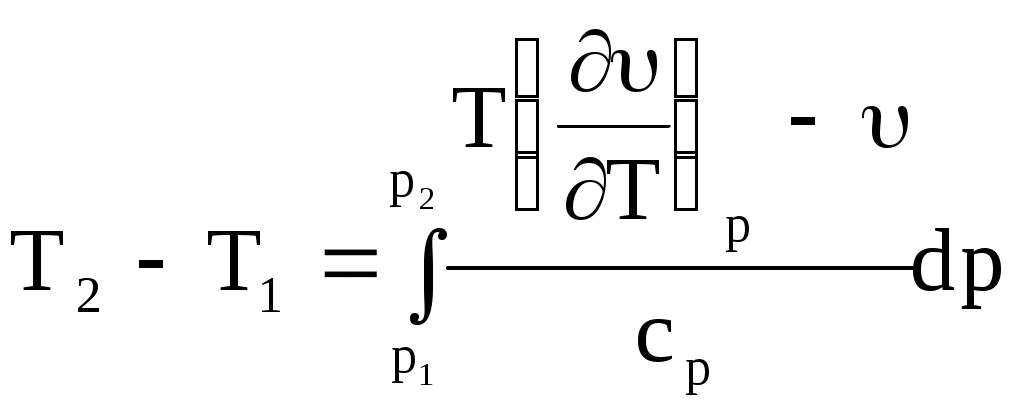 . (10.38) . (10.38)
В зависимости от начального состояния реального газа его температура при дросселировании может как уменьшаться, так и увеличиваться. Так как уменьшение температуры реального газа при дросселировании наблюдается при сравнительно пониженных начальных температурах, а ее увеличение - при повышенных начальных температурах, то при некоторой промежуточной начальной температуре газа отрицательный знак температурного эффекта при дросселировании должен изменяться на положительный.
При этой начальной температуре, называемой температурой инверсии, температура реального газа при его дросселировании не будет изменяться, т.е. при температуре инверсии реальный газ при дросселировании будет вести себя как идеальный.
Анализ уравнения (10.37) показывает, что знак dT будет зависеть от знака выражения T(/T)p - и будет ему противоположен (т.к. при дросселировании dp < 0). При этом могут быть три случая:
1) 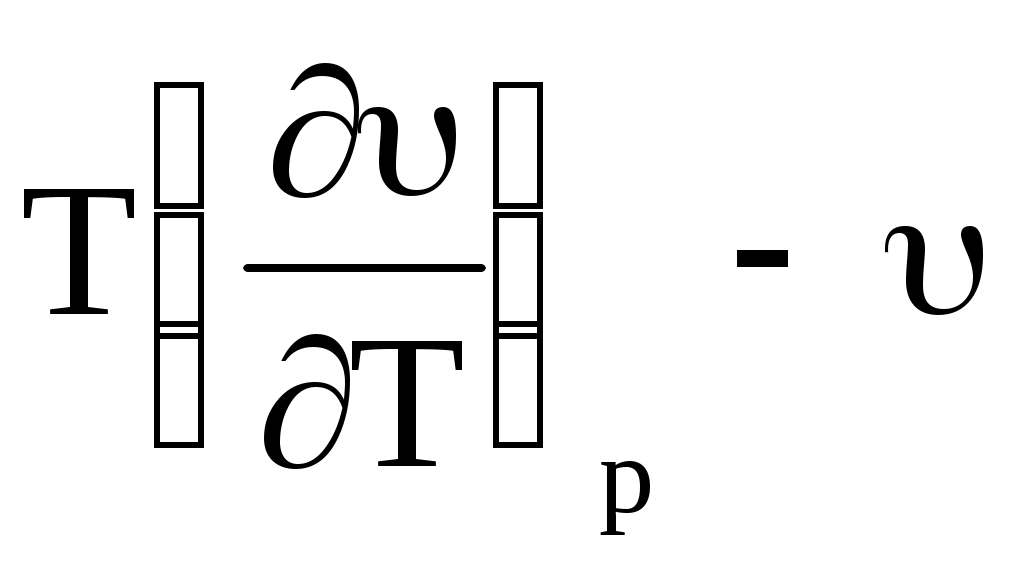 > 0 dT < 0 положительный дроссель-эффект; > 0 dT < 0 положительный дроссель-эффект;
2) 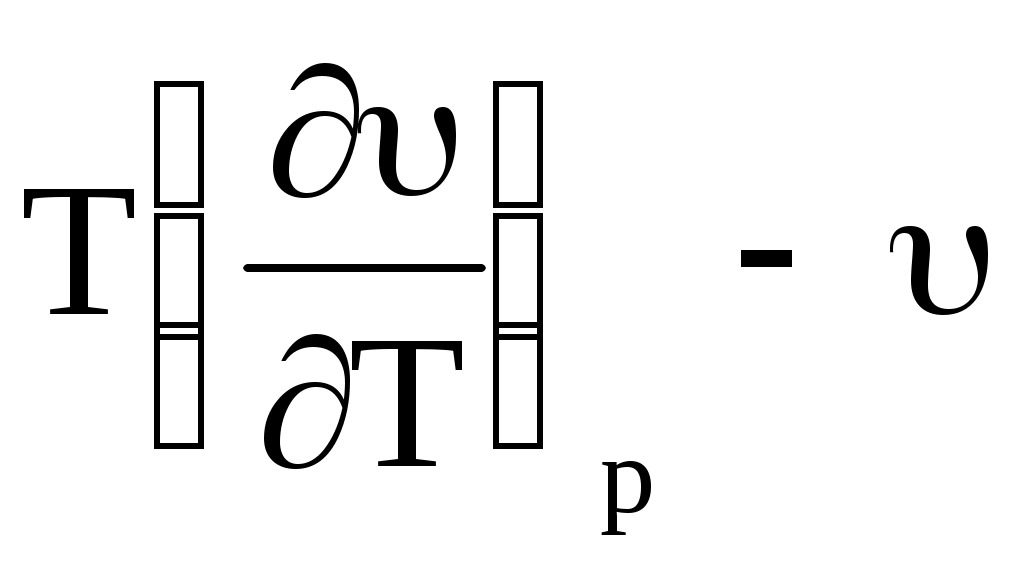 = 0 dT = 0 нулевой дроссель-эффект; = 0 dT = 0 нулевой дроссель-эффект;
3) 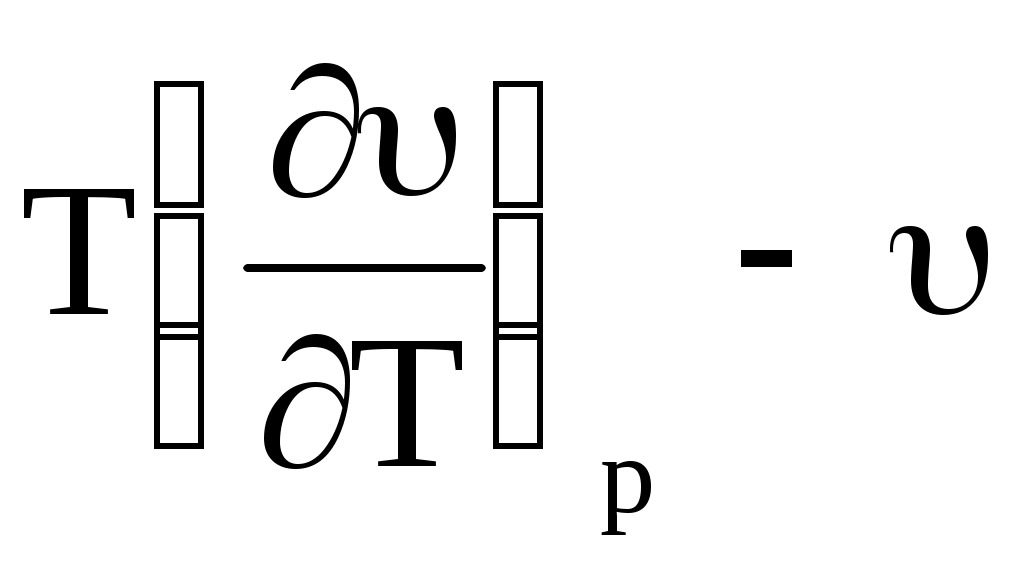 < 0 dT > 0 отрицательный дроссель-эффект. < 0 dT > 0 отрицательный дроссель-эффект.
Второй случай соответствует состоянию газа, когда его температура равна температуре инверсии, откуда температура инверсии
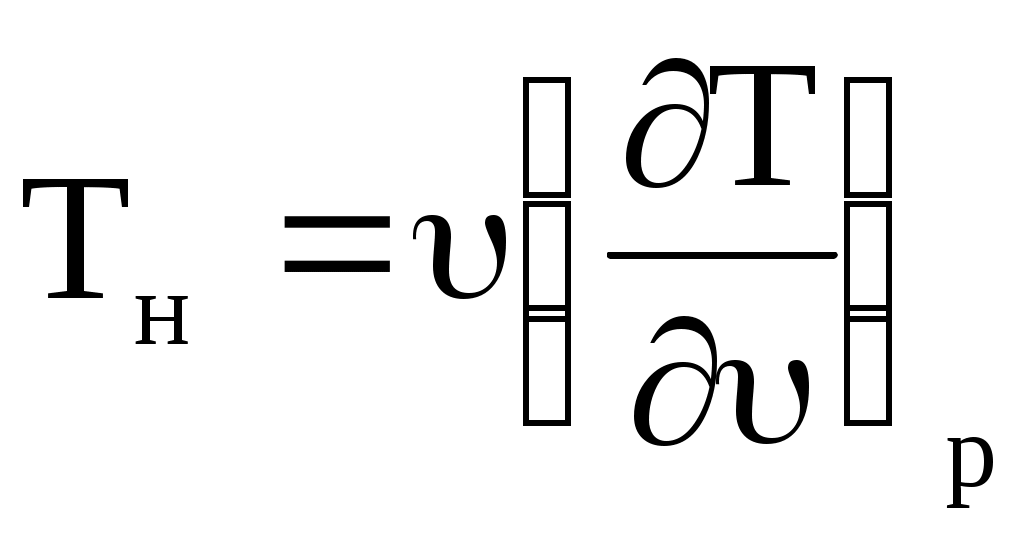 . (10.39) . (10.39)
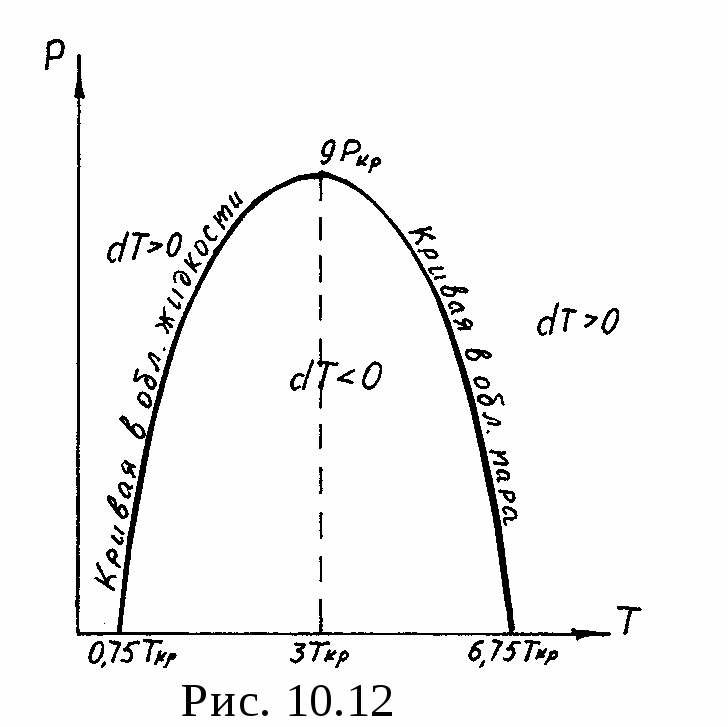
Отметим, что для каждого давления имеются две температуры инверсии: одна в области жидкости (нижняя точка инверсии), другая в области перегретого пара (верхняя точка инверсии). Температура инверсии зависит от давления, при котором находится тело. Как показывает опыт, с повышением давления температура инверсии для жидкости повышается, а для пара понижается. Совокупность точек инверсии при различных давлениях представляет графически кривую инверсии данного вещества (рис.10.12). Точки на кривой инверсии удовлетворяют уравнению (10.39). Кривая инверсии в системе координат p, T делит поле диаграммы на две области. Во внутренней области дроссель-эффект положителен (dT < 0), во внешней - отрицателен (dT > 0).
Если считать, что свойства вещества описываются уравнением Ван-дер-Ваальса, то в точке максимума кривой инверсии удельный объем равен критическому (max = кр), давление pmax = 9 pкр, температура Tmax = 3Ткр. Правая ветвь инверсионной кривой пересекает ось температур в точке Т = 6,75 Ткр, а левая - в точке Т = 0,75 Ткр.
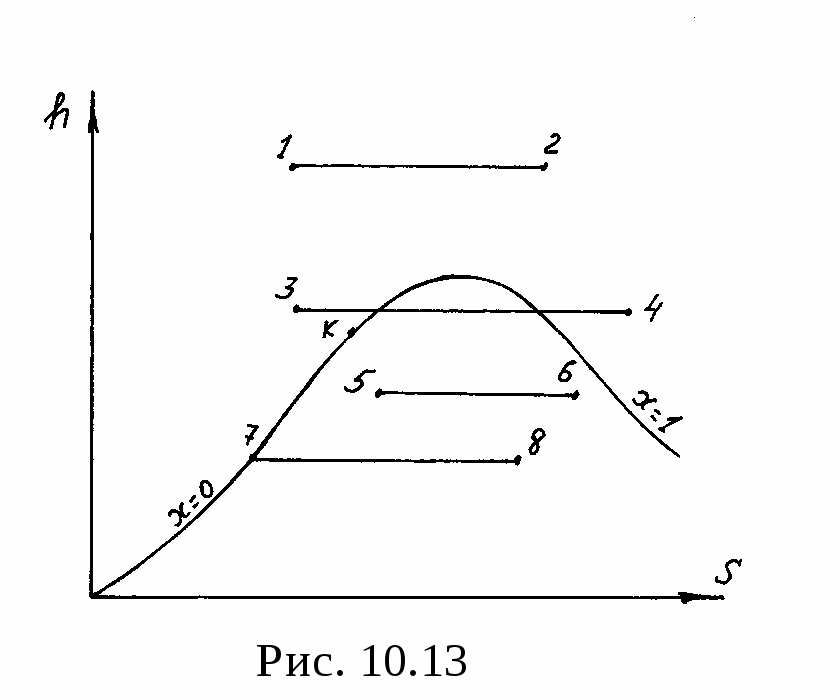
Исследование процесса дросселирования водяного пара очень наглядно производится по h, s - диаграмме водяного пара (рис. 10.13), в которой процесс дросселирования можно условно изобразить горизонтальной линией. Из диаграммы видно, что если подвергается дросселированию перегретый пар (процесс 1-2), то давление и температура уменьшаются, а объем, энтропия и степень перегрева увеличиваются. При дросселировании пара высокого давле ния и небольшого перегрева (процесс 3 - 4) пар сначала переходит в сухой насыщенный, затем во влажный, потом опять в сухой и снова в перегретый. При дросселировании влажного пара степень сухости его увеличивается (процесс
5 - 6). При дросселировании кипящей жидкости (процесс 7 - 8) она частично испаряется и переходит в состояние влажного насыщенного пара. Процесс дросселирования, как видно из рисунка, сопровождается ростом энтропии и, следовательно, уменьшением работоспособности рабочего тела.
|
 Скачать 3.21 Mb.
Скачать 3.21 Mb.