Задачи на экзамен по дискретной математике. Перечень задачи на экзамен по дискретной математике для студентов 1 курса дневного обучения по направлению Бизнесинформатика Задача 1
 Скачать 310.5 Kb.
|
|
Перечень задачи на экзамен по дискретной математике для студентов 1 курса дневного обучения по направлению «Бизнес-информатика» Задача 1. А) Из колоды карт (36 листов) вынимается сразу несколько карт. Сколько возможных исходов, что в случае, если вынуто четыре карты: Две карты будут одной масти? ровно четыре карты будут одного цвета? будут три семерки? Задачу проверить с помощью в Excel Б) С помощью алгоритма Краскала построить основный граф 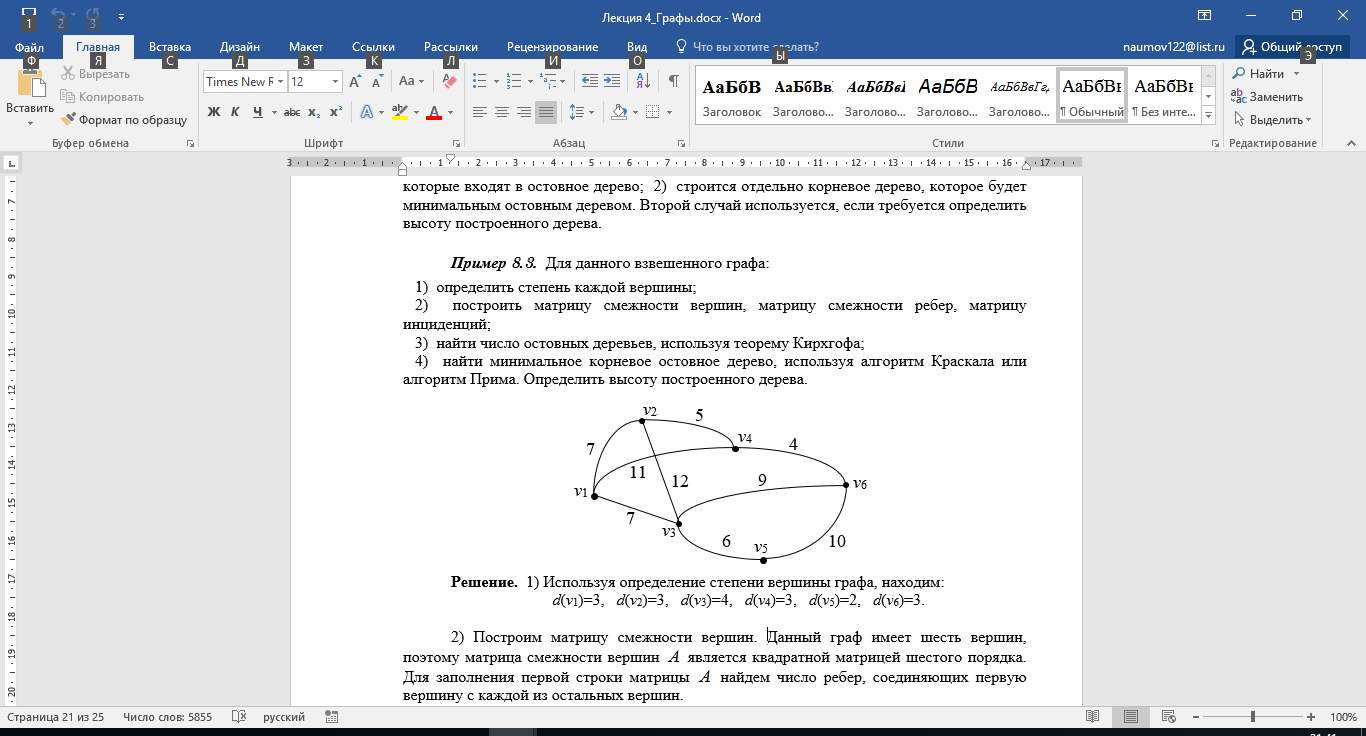 Определить длину минимального остова. Задача 2. А) Из 16 вопросов надо выбрать 4 и разместить их в четырех билетах. Сколькими способами это можно сделать, если в билете один вопрос? Сколькими способами можно выбрать 6 элементов из 10? Б) С помощью алгоритма Прима построить основный граф. Определить длину минимального остова. Задача 3. А) Преобразовать в сколемовскую нормальную форму ∃x1∀x2∀x3∃x4∀x5∃x6((P1(x1, x2, x4)∨¬P2(x3,x4,x5))&P3(x4,x6))V∃x5P4(x5). Б) Найти объединение, пересечение графов  Построить из графа лес. Задача 4. Найти степени всех вершин (степени полуисхода и степени полузахода) для графа. Построить матрицу достижимости графа. Построить остов графа. А)  Б) Построить совершенную конъюнктивную нормальную форму для функции, заданной конституентами единицы 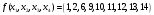 .Задача 5. Построить матрицу расстояний, найти диаметр и радиус для графа. А) Б) Построить совершенную конъюнктивную нормальную форму для функции, заданной конституентами единицы 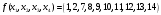 .Минимизировать данную функцию с помощью карты Карно. Задача 6. Даны множества А) 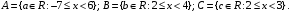 Найти 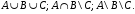 Как изменится решение задачи если элементы множества – целые числа?Б) Нарисовать орграф и построить матрицу весов его дуг для взвешенного орграфа, заданного списками дуг EG и соответствующих им весов W: EG={v1v2,v1v3,v2v3,v2v4,v3v4} , W={1,2,-1,3,1}. Задача 7. А) Даны три множества А, В, С. С помощью диаграммы Эйлера показать 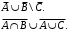 Б) Минимизировать функцию методом Квайна- МакКласки, если заданы конституенты единицы 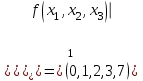 Задача 8. Докажите с помощью диаграммы Эйлера: А) 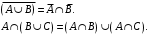 Б) Минимизировать функцию трех переменных, если она принимает единичные значения на наборах (1,2.3,4,6,7,8) по алгоритму Квайна-Маккласки. Задача 9. А) Перечислите множество всех подмножеств (булеан), если исходное множество 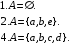 Б) Функция задана двоичным числом 11110001. Построить СДНФ и СКНФ. Найти МДНФ методом минимизирующих карт Карно. Определить исходную сложность и сложность минимальной формы. Задача 10. А) Пусть задано множество отношений 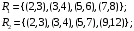 Найти 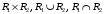 Б) Доказать методом резолюций истинность следующей клаузы: A → B, C → D, B → E, D → F, E → F, A → C ⇒ A. Задача 11. А) Построить граф и матрицу отношения эквивалентности для разбиения на классы эквивалентности 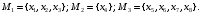 Б) Сколько различных составов команд по 11 участников можно организовать из группы 15 спортсменов? Задача 12. А) Задать отношение различными способами (матричным, графическим) 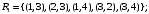 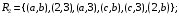 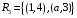 .Б) Найти с помощью алгебраических преобразований совершенную дизъюнктивную нормальную форму для функции 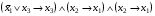 Задача 13. А) Выполнить операции над отношениями 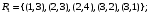 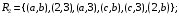 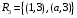. 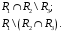Б) Построить в базисе Шеффера схему для формулы 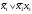 Задача 14. А) Выяснить, эквивалентны ли функции 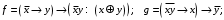 Б) Построить СДНФ для формулы x1+ x1( x3 + x2x3). Задача 15. А) Построить совершенную дизъюнктивную и конъюнктивную нормальные формы для функции, заданной конститутентами единицы 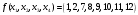 .Б) Построить совершенную дизъюнктивную нормальную форму (CДНФ) для формулы (x1x2)x3 Задача 16. А) Построить таблицу истинности функции и построить логическую схему для функции в базисе Буля 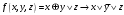 .Найти частную производную по  .Б) Доказать методом Вонга истинность следующей клаузы: 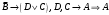 .Задача 17. А) С помощью карты Карно минимизировать функцию 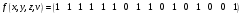 .Указать сложности минимальных ДНФ. Б) Методом каскадов построить схему функции, если в состав элементов входят двухвходовые элементы И и ИЛИ. 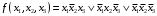 Определить ее сложность. Задача 18. Решить задачу покрытия, если А) 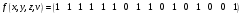Б) Построить код Шеннона-Фано для алфавита, если известно распределение час тот символов
Задача 19. А) Доказать истинность заключения 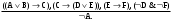 .Б) Минимизировать функцию 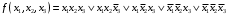 по алгоритму Квайна-Маккласки.Задача 20. А) Дано P1(x):= «x – студент», P2(x, y):= «x обучается в университете y», P3(x):= «x имеет зачетную книжку», М – множество индивидов, Y – множество учебных заведений, xM, yY – предметные переменные. С помощью предикатов составить формулы высказываний: Существуют студенты (x) некоторых университетов (y), которые не имеют зачетной книжки. Все студенты имеют зачетные книжки. Все студенты всех университетов имеют зачетные книжки». Б) Построить матрицу Кирхгофа для графа 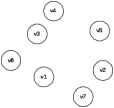 Задача 21. А) Система кодирования имеет ви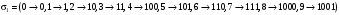д:  Проверить неравенство Макмиллана и построить равномерный и префиксный код.Б) Минимизировать функцию с помощью карты Карно 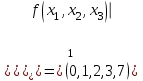Задача 22. А) С помощью алгоритма Хаффмана построить код, если исходный код имеет вид:
Проанализировать среднюю длину кода символа для полученной кодировки. Б) Найти совершенную дизъюнктивную нормальную форму для функции 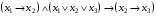 Задача 23. А) Построить в базисе Вебба схемную реализацию формулы 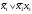Б) Найти совершенную дизъюнктивную нормальную форму для функции 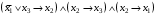 .Задача 24. А) Преобразовать в сколемовскую нормальную форму ∃x1∀x2∀x3∃x4∀x5∃x6((P1(x1, x2)∨¬P2(x3,x4,x5))&P3(x4,x6)). Б) Преобразовать в 8, 2 и 16 системы счисления число 23,22. Задача 25. А) С помощью метода каскадов синтезировать логическую схему 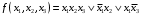 Б) Проверить, является ли код разделимым с помощью неравенства Макмиллана
Задача 26. А) Привести к предваренной нормальной форме ∃x∃y(P1(х, y))&( ∀x∃y(P2(x, y))). Б) Найти производную по x1, x2 от функции 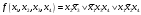 Задача 27. А) С помощью алгоритма Дейкстры найти минимальное расстояние от истока вершины 1 до вершины 6. 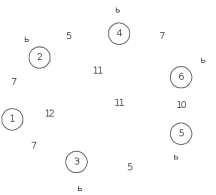 Б) Найти совершенную дизъюнктивную нормальную форму для функции 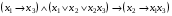 Задача 28. А) С помощью алгоритма Хаффмана построить код, если исходный код имеет вид:
Проанализировать среднюю длину кода символа для полученной кодировки. Сравнить с равномерным кодом Б) Найти совершенную дизъюнктивную нормальную форму для функции 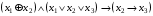 Задача 29. А) Преобразовать в сколемовскую нормальную форму ∃x1∀x2∀x3∃x4∀x5 ((P1(x1, x2)∨¬P2(x3,x4,x5))&P3(x4,x6)). Б) Найти совершенную дизъюнктивную нормальную форму для функции 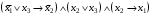 .Задача 30. А) Преобразовать в сколемовскую нормальную форму ∃x1∀x2∀x3∃x4∀x5∃x6((Q1(x1, x2,x3)∨¬P2(x3,x4,x5))&P3(x4,x6)). Б) Преобразовать в 8, 2 и 16 системы счисления число 33,22, заданное в десятичной системе счисления. Задача 31. А) С помощью метода каскадов синтезировать логическую схему 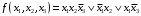 Б) Проверить, является ли код разделимым с помощью неравенства Макмиллана
Закодировать с помощью этого кода сообщение 12350 Задача 32. А) Привести к склолемовской нормальной форме ∃x∃y(P1(х, y))&( ∀x∃y(P2(x, y))). Б) Найти производную по x1, x2 от функции 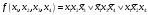 Задача 33. А) С помощью алгоритма Дейкстры найти минимальное расстояние от истока вершины 1 до вершины 6. 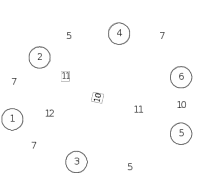 Б) Найти совершенную дизъюнктивную нормальную форму для функции 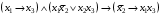 Руководитель образовательного направления В. Наумов |