заболеваниях глаз. Передаточные механизмы
 Скачать 467.83 Kb. Скачать 467.83 Kb.
|
|
Первый ролик ПЕРЕДАТОЧНЫЕ МЕХАНИЗМЫ Передаточные механизмы передают движение от одного тела к другому. Параметры движения тел определяются с учётом параметров точек соприкосновения (зацепления) этих тел. На рисунке 1 (а, б, в, г) приведены различные схемы передачи движения от одного тела к другому. На рисунках 1,а и 1,б зависимости угловых скоростей колёс определяются из соотношения 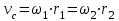 , т.е. , т.е.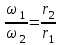 . . 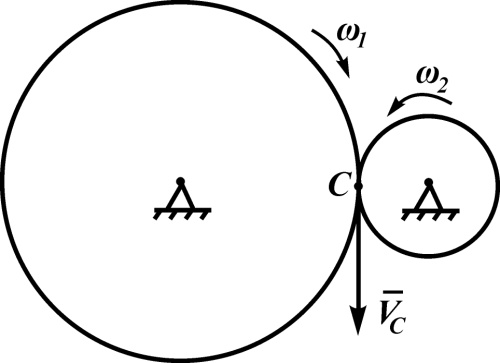 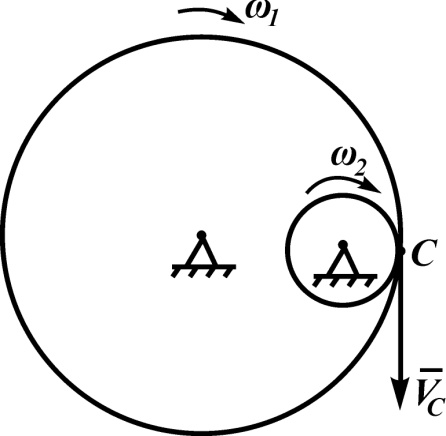 а б 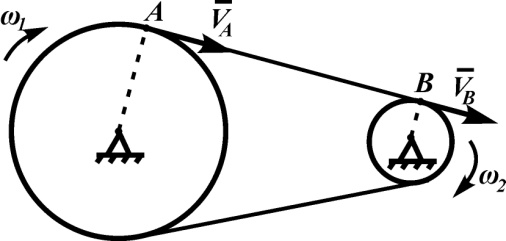 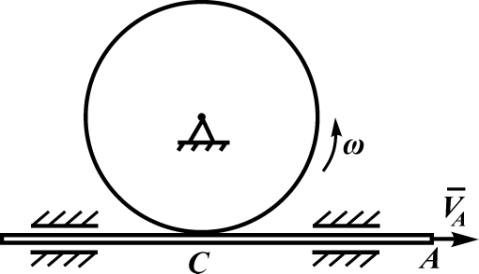 в г Рисунок 1 На рисунке 1,а (внешнее зацепление) колёса вращаются в противоположные стороны, на рисунке 1,б (внутреннее зацепление) колёса вращаются в одну сторону. На рисунке 1,в показана цепная или ремённая передача. Скорости точек 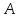 и и 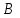 цепи или ремня должны быть равны соответственно скоростям точек цепи или ремня должны быть равны соответственно скоростям точек 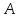 и и 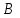 , принадлежащих шкивам: , принадлежащих шкивам: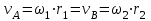 , , 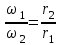 . .На рисунке 1,г поступательное движение стержня обеспечивает вращение колеса: 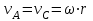 , , 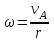 . .На рисунке 2 изображена фрикционная передача: колесо 1, прижимаясь к торцу колеса 2 в точке 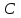 , обеспечивает его вращение вокруг вертикальной оси, , обеспечивает его вращение вокруг вертикальной оси,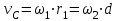 , , 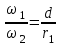 . .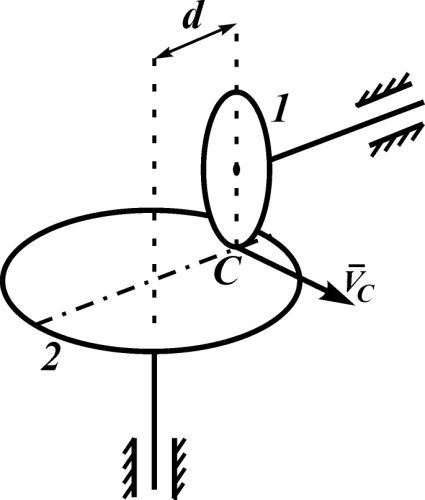 Рисунок 2 Рядовая передача – это передача, в которой все оси колёс, находящихся в зацеплении, неподвижны (рисунок 3). 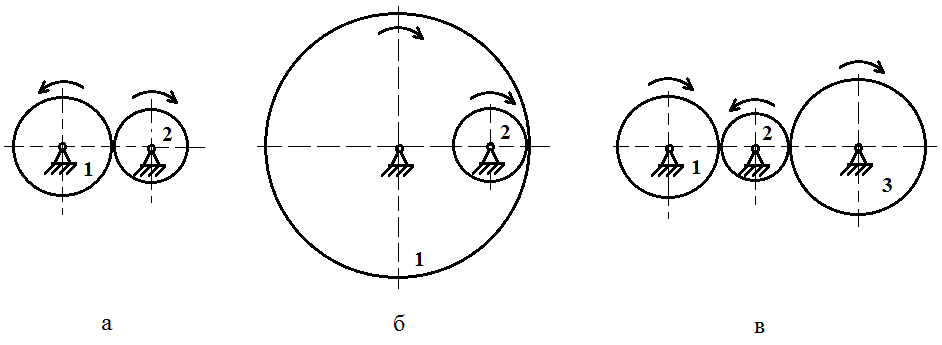 Рисунок 3 При внешнем зацеплении колёса вращаются в разные стороны, при внутреннем зацеплении – в одну сторону. При этом 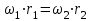 . Для случаев, изображённых на рисунке 3: . Для случаев, изображённых на рисунке 3:а) 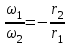 ; б) ; б) 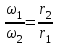 ; ; в) 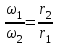 , , 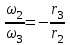 , , 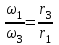 . .В случае (в) отношение угловых скоростей не зависит от радиуса промежуточных колёс, которые называются паразитными (колесо 2). Для рядовой передачи с числом колёс n и числом внешних зацеплений k справедлива формула: 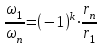 (*). (*).Передаточным числом данной передачи называется величина 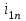 , определяемая отношением угловой скорости ведущего колеса к угловой скорости ведомого: , определяемая отношением угловой скорости ведущего колеса к угловой скорости ведомого: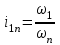 . .Передаточные механизмы с одной степенью свободы, в числе звеньев которых имеются колёса с подвижными осями, называются планетарными (рисунок 4). Колёса с неподвижными осями называются солнечными или центральными, а с подвижными осями – планетарными колёсами или сателлитами. Кривошип, несущий на себе оси сателлитов, называется поводком или водилом. 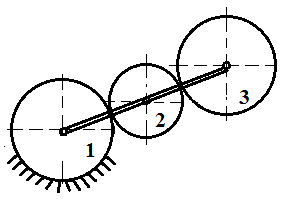 Рисунок 4 Передача называется дифференциальной, если все колёса являются подвижными и могут вращаться вокруг своей оси независимо от водила. Второй ролик РАСЧЁТ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ Расчёт планетарных и дифференциальных механизмов производится разными способами. 1. С помощью мгновенных центров скоростей. В случаях, когда передачи цилиндрические, т.е. оси колёс параллельны, движение механизма можно рассматривать как плоскопараллельное. Задача 1 В планетарном механизме (рисунок 1) колёса 1, 2, 3 имеют радиусы 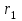 , , 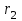 , , 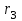 . Колесо 1 неподвижно. Водило АВ вращается с угловой скоростью . Колесо 1 неподвижно. Водило АВ вращается с угловой скоростью 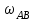 . Определить угловую скорость . Определить угловую скорость 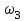 колеса 3. колеса 3.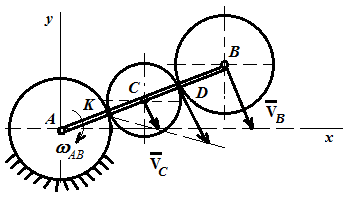 Рисунок 1 Решение Определяем скорости центров подвижных колёс 2 и 3: 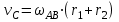 , , 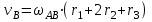 . .Точка К зацепления колёс 1 и 2 неподвижна, поэтому она является мгновенным центром скоростей (МЦС) для колеса 2. Тогда 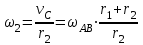 . .Определим скорость точки D зацепления колёс 2 и 3 как точки, принадлежащей второму колесу: 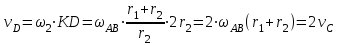 . .В зависимости от соотношения радиусов 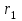 , , 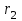 , , 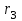 мгновенный центр скоростей колеса 3 будет располагаться на линии, проходящей через АВ, либо правее точки В ( мгновенный центр скоростей колеса 3 будет располагаться на линии, проходящей через АВ, либо правее точки В (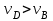 ), либо левее точки D ( ), либо левее точки D (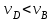 ). ).Определим расстояние по оси x от точки В до МЦС колеса 3 и угловую скорость колеса 3: 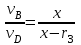 ; ;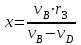 ; ;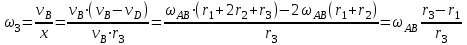 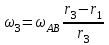 . .При 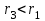 вращение будет противоположно вращение будет противоположно 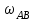 ; ;при 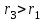 вращение третьего колеса будет в ту же сторону, что и АВ; вращение третьего колеса будет в ту же сторону, что и АВ;при 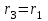 третье колесо будет двигаться поступательно ( третье колесо будет двигаться поступательно (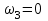 ). ).2. С помощью метода остановки (метода Виллиса). Пусть 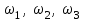 – абсолютные угловые скорости колёс 1, 2 и 3; – абсолютные угловые скорости колёс 1, 2 и 3; 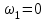 . Сообщим плоскости xAy вращение с угловой скоростью . Сообщим плоскости xAy вращение с угловой скоростью 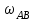 , но в противоположную сторону по отношению к водилу АВ. По отношению к этой плоскости для всех колёс угловые скорости будут равны , но в противоположную сторону по отношению к водилу АВ. По отношению к этой плоскости для всех колёс угловые скорости будут равны 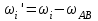 : :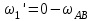 ; ;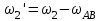 ; ;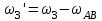 ; ;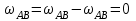 . .В данном предположении оси колёс неподвижны. Число внешних зацеплений k=2. Тогда получаем 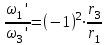 или или 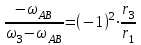 ; ; 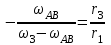 ; ;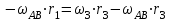 ; ; 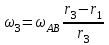 . .Направления вращения определяются аналогично первому случаю. Задача 2 Определить угловую скорость 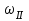 на выходе редуктора (рисунок 2). на выходе редуктора (рисунок 2).Дано: 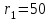 см, см, 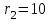 см, см, 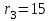 см, см, 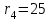 см, см, 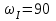 с-1, с-1, 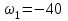 с-1. с-1. 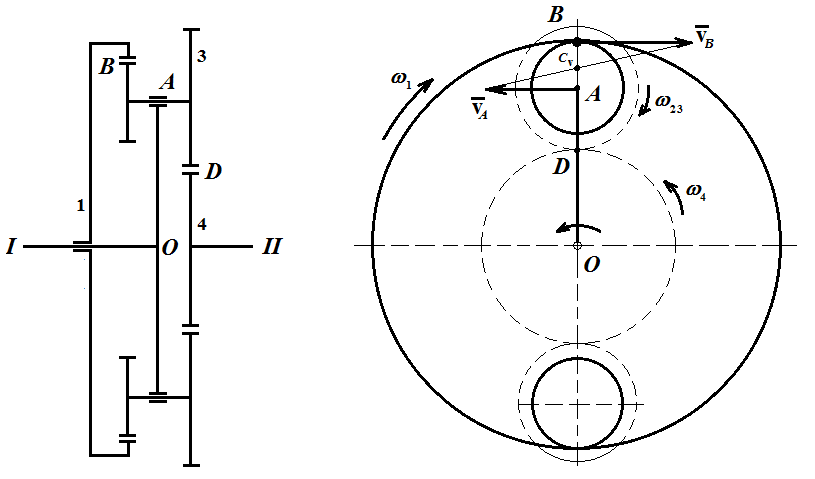 Рисунок 2 Решение_Угловые_скорости_деталей_механизма_можно_определить_двумя_способами:1)_с_помощью_законов_плоского_движения.Скорость_точки_А'>Решение Угловые скорости деталей механизма можно определить двумя способами: 1) с помощью законов плоского движения. Скорость точки А 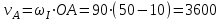 см/с. см/с.Скорость точки В 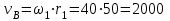 см/с. см/с.Мгновенный центр скоростей сателлита – Сv. Составим пропорцию 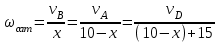 ; ; 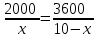 ; ;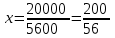 см; см;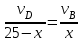 ; ;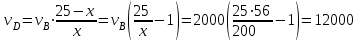 см/с; см/с;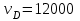 см/с; см/с;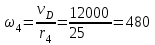 с-1; с-1; 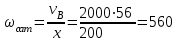 с-1; с-1;2) с помощью теории сложения вращений твёрдого тела (метод Виллиса). Колёса редуктора участвуют в относительном вращении по отношению к водилу и в переносном вращении вместе с водилом вокруг его оси. Переносной угловой скоростью для каждого колеса является угловая скорость водила. Относительные угловые скорости колёс определяются как разности абсолютных и переносных угловых скоростей: 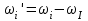 ; ; 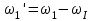 ; ;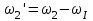 ; ;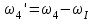 ; ;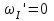 . .Эти относительные скорости являются угловыми скоростями колёс при мысленной остановке водила, т.е. получаем рядовую передачу с передаточным числом 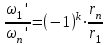 . .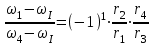 ; ; 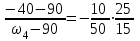 ; ;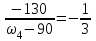 ; ; 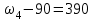 ; ; 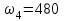 с-1. с-1.Определим угловые скорости сателлитов: 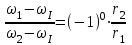 ; ; 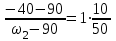 ; ; 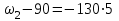 ; ;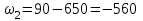 с-1; с-1;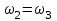 , т.е. вращение происходит по ходу часовой стрелки. , т.е. вращение происходит по ходу часовой стрелки.Рассмотрим примеры, в которых оси вращения пересекаются. Задача 3 Определить абсолютную угловую скорость шестерни 1, находящейся в коническом зацеплении с неподвижной шестернёй 2 (рисунок 3, а). Дано: 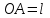 , , 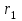 , , 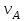 (вектор направлен к нам). (вектор направлен к нам).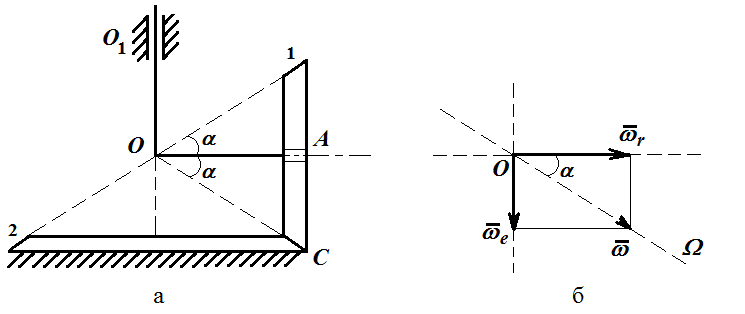 Рисунок 3 Решение Результирующее (абсолютное) вращение шестерни 1 является результатом сложения двух вращений: переносного вместе с водилом ОА и относительного вокруг водила ОА, 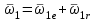 . .Переносная угловая скорость 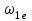 может быть определена из соотношения может быть определена из соотношения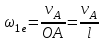 . .Это вращение происходит вокруг оси ОО1. Кроме того, видно, что колесо 1 вращается вокруг собственной оси, а абсолютное вращение происходит вокруг оси, проходящей через неподвижные точки О и С (мгновенные оси). Следовательно, можно построить треугольник угловых скоростей, в котором линии, по которым направлены векторы угловых скоростей, известны, также известен модуль одной из скоростей. С помощью известных величин 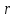 и и 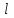 из треугольника угловых скоростей определим угол из треугольника угловых скоростей определим угол 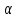 : :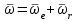 ; ;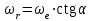 ; ; 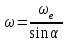 ; ; 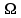 – мгновенная ось вращения. – мгновенная ось вращения.При постоянных угловых скоростях 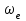 и и 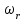 можно найти угловое ускорение можно найти угловое ускорение 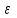 – скорость конца вектора угловой скорости: – скорость конца вектора угловой скорости: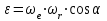 , ,вектор 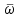 описывает своим концом окружность радиуса описывает своим концом окружность радиуса 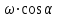 или или 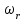 . .Задача 4 Дан двойной дифференциальный механизм (рисунок 4). Колёса 1 и 2 вращаются с угловыми скоростями 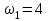 с-1 и с-1 и 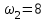 с-1. Радиусы колёс с-1. Радиусы колёс 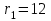 см, см, 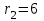 см; радиусы сателлитов см; радиусы сателлитов 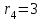 см, см, 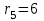 см. см. Определить угловые скорости 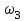 , , 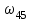 . .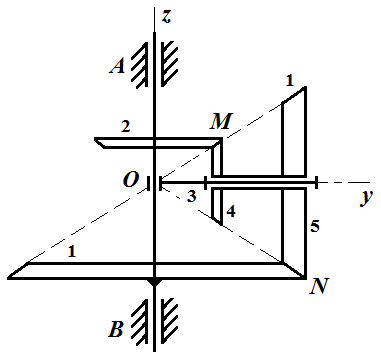 Рисунок 4 Решение Колёса 1 и 2 вращаются против часовой стрелки, если смотреть сверху вниз по линии АВ. Так же, как и в случае с параллельными осями, возможно решение несколькими способами: 1) с помощью законов плоского движения (рисунок 5, а). Скорости точек M и N, принадлежащих колёсам 2 и 1: 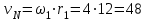 см/с; см/с; 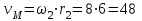 см/с. см/с.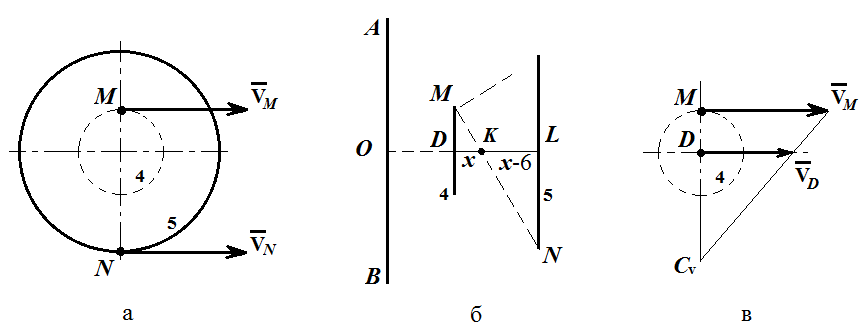 Рисунок 5 Скорости точек M и N одинаковы, т.е. точки сателлита, лежащие на линии MN, имеют одинаковые скорости, в том числе точка К, лежащая на оси (звено 3). В абсолютном движении точка К движется вместе с вращающимся водилом 3 вокруг оси АВ. 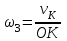 . .Для определения ОК составим пропорцию (рисунок 5, б) 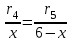 ; ; 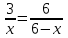 ; ; 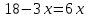 ; ;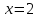 ; ; 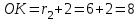 ; ;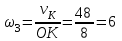 с-1 – угловая скорость водила. с-1 – угловая скорость водила.Рассмотрим шестерню 4 сателлита (рисунок 5, в): скорость её точки М известна и равна 48 см/с, скорость точки D, лежащей на шестерне 4 и оси сателлита 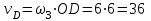 см/с. см/с.Мгновенный центр скоростей при вращении сателлита вокруг оси лежит в точке Сv: 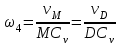 ; ;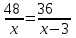 ; ;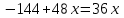 ; ; 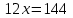 ; ;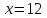 ; ; 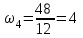 ; ;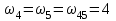 с-1. с-1.Таким образом, при вращении шестерни 4, а также шестерни 5, относительно водила её угловая скорость 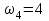 с-1; с-1;2) с помощью теории сложного движения (рисунок 6). 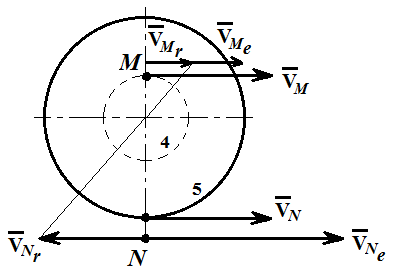 Рисунок 6 Скорости точек M и N, принадлежащих колёсам 2 и 1: 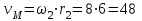 см/с; см/с;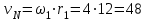 см/с. см/с.Движение точек M и N может быть разложено на переносное (вращение вместе с водилом) и относительное (вращение вокруг водила). Поскольку вращения колёс происходят в одну сторону, то можно предположить, что и вращение водила будет происходить в ту же сторону и, следовательно, векторы переносных скоростей точек M и N будут направлены как 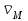 и и 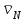 ( (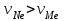 ). ). На рисунке 6 показаны направления векторов относительных скоростей 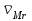 и и 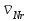 . Определим модули абсолютных скоростей точек M и N: . Определим модули абсолютных скоростей точек M и N: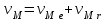 , , 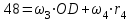 ; ;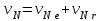 , , 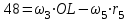 ; ;Помня о том, что 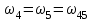 , получим , получим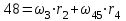 ; ; 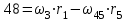 ; ;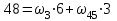 ; ; 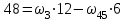 ; ;или 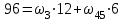 ; ;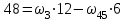 ; ;Сложим два уравнения 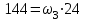 ; ; 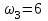 с-1; с-1; 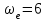 с-1; с-1;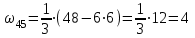 с-1; с-1; 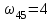 с-1; с-1; 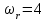 с-1. с-1.Положительные знаки в ответах говорят о правильности сделанных предположений; 3) с помощью метода Виллиса. Поскольку оси вращений пересекаются, то алгебраически складывать угловые скорости нельзя. Знаки передаточного числа определяются следующим образом: - выбираем положительные направления осей (в данном случае Oz и Oy); - смотря навстречу осям, определяем вращение колёс, находящихся в зацеплении: если колёса вращаются в одну сторону, то знак передаточного числа «+», если в разные стороны – то «–». Остановим мысленно водило и получим рядовое зацепление. Для пары колёс 1 и 5 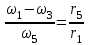 ; ;для колёс 4 и 2 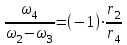 . .Перемножим последние выражения и, учитывая 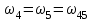 , получим , получим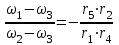 ; ; 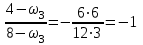 ; ;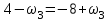 ; ; 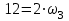 ; ; 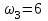 с-1. с-1.Относительная угловая скорость сателлитов 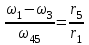 ; ; 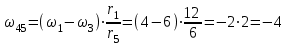 ; ;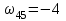 с-1; с-1;т.е. вращение происходит по часовой стрелке, если смотреть с конца положительного направления оси Oy. Абсолютную угловую скорость сателлитов можно найти, сложив 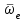 и и 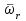 , т.е. , т.е. 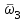 и и  . . |
