Электротехника Контрольная работа Вариант 11 Переходные процессы в линейных электрических цепях. 11 вариант. Переходные процессы в линейных электрических цепях
 Скачать 103.9 Kb. Скачать 103.9 Kb.
|
|
Контрольная работа на тему «Переходные процессы в линейных электрических цепях» Дана электрическая цепь, в которой происходит коммутация (рис. 4.20). В цепи действует постоянная ЭДС Е. Параметры цепи приведены в табл. 4.1. Требуется определить закон изменения во времени напряжения на резисторе R2. Задачу следует решать классическим методом расчета. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени в интервале от t=0 до t=3/|p|min, где |p|min – меньший по модулю корень характеристического уравнения. 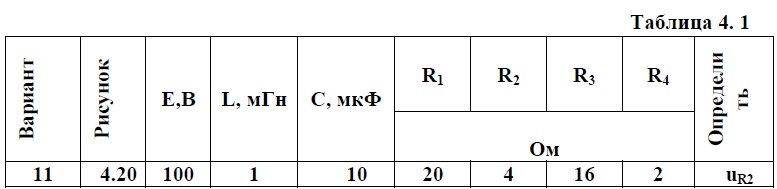 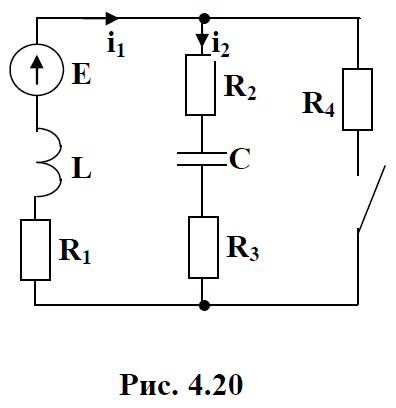 Расчет классическим методом Независимые начальные условия: Катушка будет являться участком провода с сопротивлением0. Конденсатор будет являться местом разрыва цепи. Поэтому расчетная схема для данного режима принимает вид: 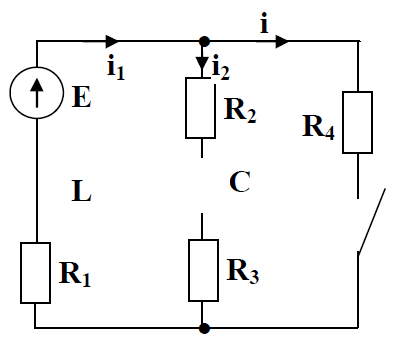 Рассчитаем (независимые начальные условия) токи и напряжения до коммутации: Е = 100 В 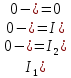 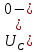 По законам коммутации: 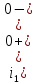 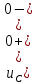 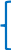 Чтобы определить Чтобы определить 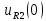 , составим систему уравнений по второму закону Кирхгофа для схемы после коммутации: , составим систему уравнений по второму закону Кирхгофа для схемы после коммутации: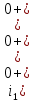 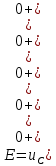 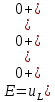 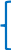 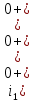 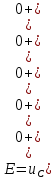 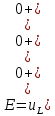 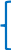 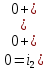 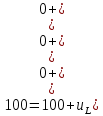 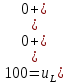 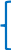 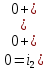 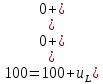 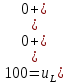 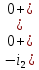 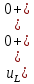 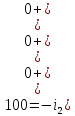 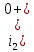 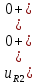 Переходное напряжение на резисторе R2 определим по формуле: 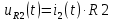 Где 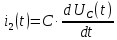 Переходное напряжение на конденсаторе С в общем виде: 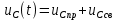 где 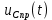 – принужденная (вынужденная) составляющая; – принужденная (вынужденная) составляющая;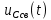 – свободная составляющая. – свободная составляющая.Вынужденная (принужденная) составляющая напряжения определяется как установившееся значение после коммутации для t→∞. 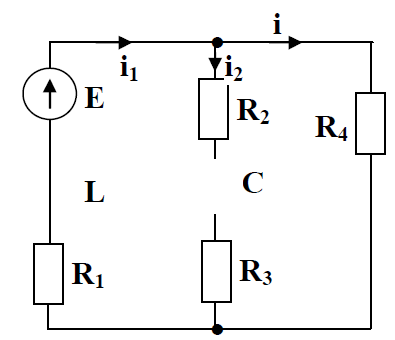 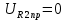 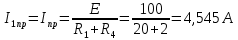 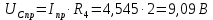 Для определения свободной составляющей напряжения 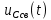 , рассчитаем корни характеристического уравнения р1 и р2 . , рассчитаем корни характеристического уравнения р1 и р2 .Для этого составим выражение для входного сопротивления пассивной цепи после коммутации: 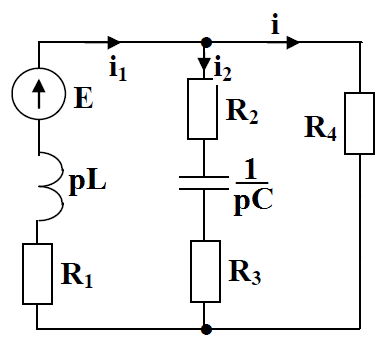 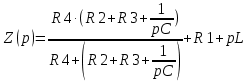 Подставим известные величины и определим корни уравнения: 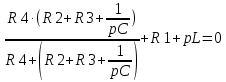 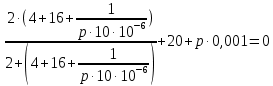 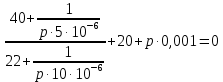 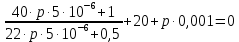 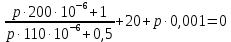 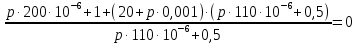 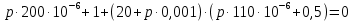 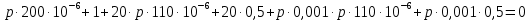 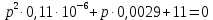 После решения квадратного уравнения получим корни: р1 = -4 593,43 р2 = -21 770,2 Таким образом, свободная составляющая напряжения uR2 в общем виде: 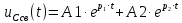 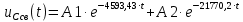 Переходное напряжение на конденсаторе С в общем виде: 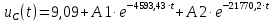 Для того чтобы определить постоянные интегрирования А1 и А2, рассмотрим эти выражения в момент t=0: 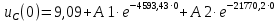 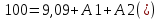 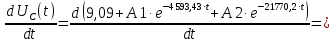 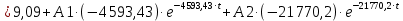 Для того чтобы определить постоянные интегрирования А1 и А2, рассмотрим и это выражения в момент t=0: 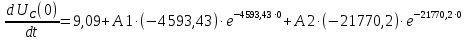 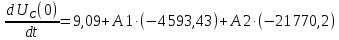 Так как 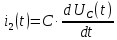 то 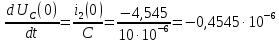 Получим: 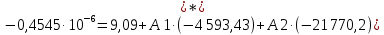 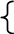 Решим полученную систему двух уравнений (*) и (**) и определим А1 и А2: Решим полученную систему двух уравнений (*) и (**) и определим А1 и А2: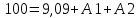 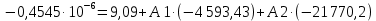 А1 = 88,758 А2 = 2,152 Таким образом во время переходного процесса напряжение на конденсаторе имеет вид: 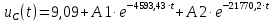 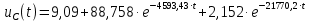 Ток в ветви с конденсатором: 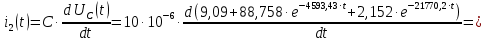 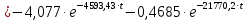 Переходное напряжение на резисторе R2 определим по формуле: 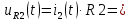 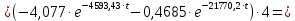 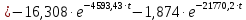 график изменения напряжение на резисторе R2 в функции времени в интервале от t=0 до t=3/|p|min, где |p|min = 4593,43 – меньший по модулю корень характеристического уравнения: 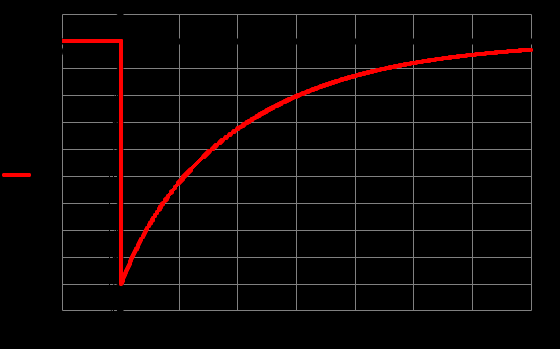 |
