Щлдд. Пересечение проецирующей прямой с плоскостью общего положения
 Скачать 169.17 Kb. Скачать 169.17 Kb.
|
|
10. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ Рассмотрение этого типа задач начинаем с частных случаев пересечения прямой с плоскостью. Пересечение проецирующей прямой с плоскостью общего положения 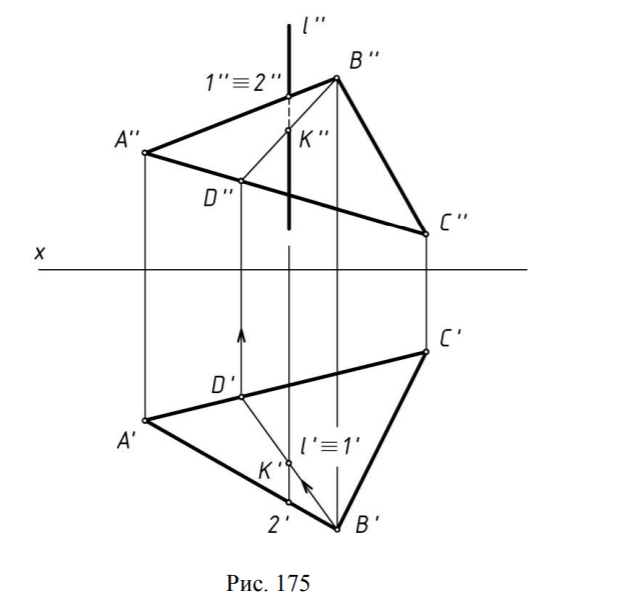 На рис.175 задана проецирующая прямая l и плоскость общего положения α треугольником АВС. Прямая l — горизонтально проецирующая, все точки которой на горизонтальную плоскость проекций π1 проецируются в вырожденную проекцию l', включая проекцию точки пересечения К'. Т.к. точка К принадлежит плоскости треугольника АВС, то по условиям принадлежности она должна принадлежать линии этой плоскости. Проведем через точку К' прямую B'D' в плоскости треугольника. Три точки — B, D и K — принадлежат одной прямой треугольника ABC. Построив фронтальную проекцию отрезка BD — B''D'', находим фронтальную проекцию точки пересечения — К''. Для придания чертежу большей наглядности необходимо определить видимость прямой до и после точки пересечения с плоскостью, которую считаем непрозрачной. Те точки прямой, которые будут ближе к наблюдателю чем точки плоскости, изображаются основными линиями. Это можно определять по конкурирующим точкам — двум точкам, принадлежащим разным геометрическим фигурам, но проекции которых на одной из плоскостей проекций совпадают. В нашем примере это точки 1 и 2. Точка 1 принадлежит прямой l, а точка 2 принадлежит отрезку АВ треугольника АВС. Фронтальные проекции этих точек совпадают (1'' = 2''). Расстояние от этих точек до наблюдателя будет определяться координатой y. 102 Точка с большей координатой будет видимой, т.е. y2> y1 и точка 2 на π2 будет видимой вместе с отрезком АВ. Отрезок 1К прямой l будет невидимым на фронтальной проекции. Следует помнить, что, как правило, проекция точки пересечения прямой с плоскостью (поверхностью) делит изображение проекции прямой на видимую и невидимую часть. Невидимая часть прямой изображается штриховой линией. Пересечение прямой общего положения с проецирующей плоскостью 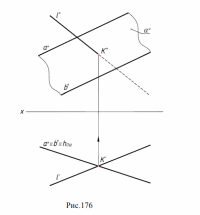 На рис.176 даны прямая l и плоскость α, заданная параллельными прямыми a и b и перпендикулярная горизонтальной плоскости проекций π1. Все точки, принадлежащие плоскости α, на горизонтальную плоскость проекций π1 спроецируются в вырожденную проекцию плоскости — прямую, совпадающую со следом этой плоскости hoα. Поэтому горизонтальная проекция точки пересечения прямой l с плоскостью определяется как точка пересечения hoα и l' — получаем проекцию К'. Фронтальную проекцию К'' определяем по принадлежности прямой l. Видимость проекции прямой l'' на фронтальной плоскости проекций определяем по конкурирующим точкам подобно предыдущему примеру. На горизонтальной плоскости проекций проекция прямой l' видимая до и после точки пересечения. Поэтому в предыдущем примере мы оговорили, что «как правило», проекция точки пересечения прямой с плоскостью (поверхностью) делит изображение проекции прямой на видимую и невидимую часть». В нашем случае это исключение из правил. 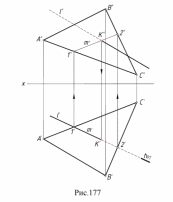 Пересечение прямой общего положения с плоскостью общего положения На рис.177 рассмотрена задача пересечения прямой l и плоскости общего положения α, заданной треугольником АВС. В этом случае решение задачи сводится к следующему алгоритму: Прямую l заключаем во вспомогательную проецирующую плоскость ( в нашем случае, в горизонтально проецирующую, заданную следом ho) Строим линию пересечения m плоскостей α (ΔABC) и по двум общим 1 и 2. Точка 1 — результат пересечения отрезка АС с плоскостью , точка 2- пересечения BC c плоскостью (как в случае пересечения прямой общего положения с проецирующей плоскостью). На фронтальной плоскости проекций находим точку К пересечения прямых l и m как принадлежащих одной плоскости . |
