Практическое занятие 2. Персептрон возможности классификации образов, задача xor
 Скачать 4 Mb.
|
|
Практическое занятие 2 Тема: Персептрон - возможности классификации образов, задача XOR Цель: Моделирование в Python двух классов линейно-разделимых образов разделяющей прямой. Полносвязная НС со ступенчатой активационной функцией выглядит следующим образом: 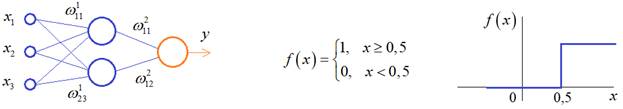 Такими были первые нейронные сети, предложенные Френком Розенблаттом в 1957 году. Рассмотрим простейший персептрон для задачи классификации двух классов образов, представленных двумя характеристиками: 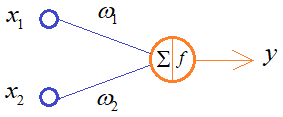 : С активационной функцией: 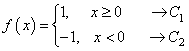 То есть, если значение суммы больше или равно 0, то вектор принадлежит классу 1:  иначе, классу 2:  Это может быть разделение на кошек и собак, на мужчин и женщин, на наличие сигнала и его отсутствие и т.п. Мы здесь обобщаем все эти случаи и представляем их в виде двух классов:  .Далее, из вида активационной функции видно, что граница разделения двух классов проходит на уровне 0. То есть, если: 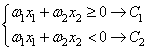 Значит, сумма:  определяет границу разделения одного класса образов от другого. Ее еще можно записать в виде:  То есть, это прямая с угловым коэффициентом  проходящая через начало системы координат: 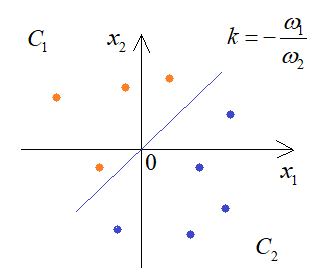 И все точки по одну сторону от этой прямой будут относиться к одному классу, а по другую сторону – к другому классу. Такая прямая получила название разделяющей прямой. (В многомерном случае она превращается в гиперплоскость и называется разделяющей гиперплоскостью). Этот двумерный график хорошо демонстрирует возможность правильной классификации простейшим персептроном только линейно-разделимых образов. Чтобы все было понятнее, давайте в качестве примера смоделируем в Python два класса линейно-разделимых образов разделяющей прямой:  то есть, прямой, идущей под 45 градусов к осям координат. В этом случае, для корректной классификации, мы должны выбрать веса нейронной сети равными, но с противоположными знаками: 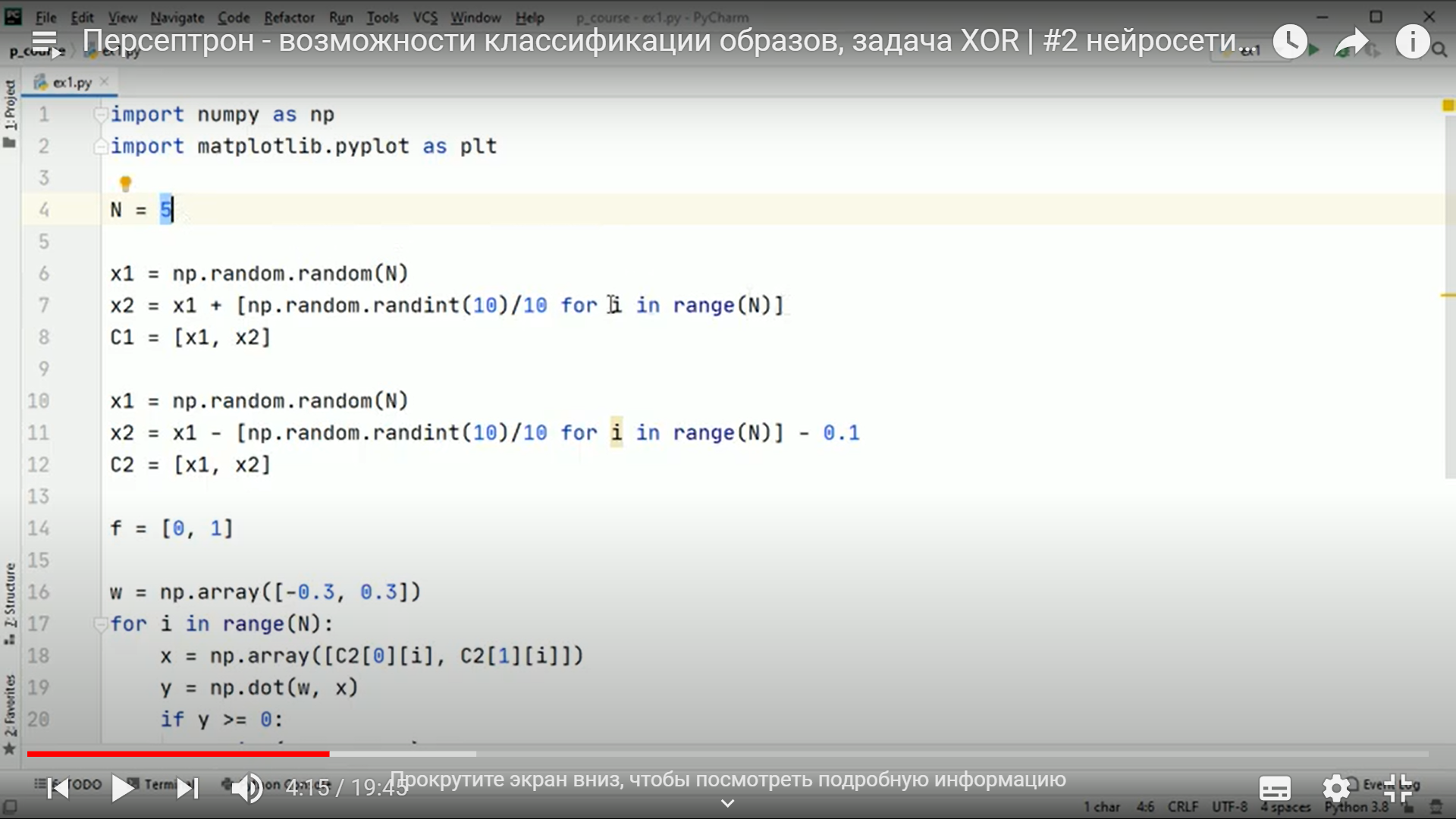 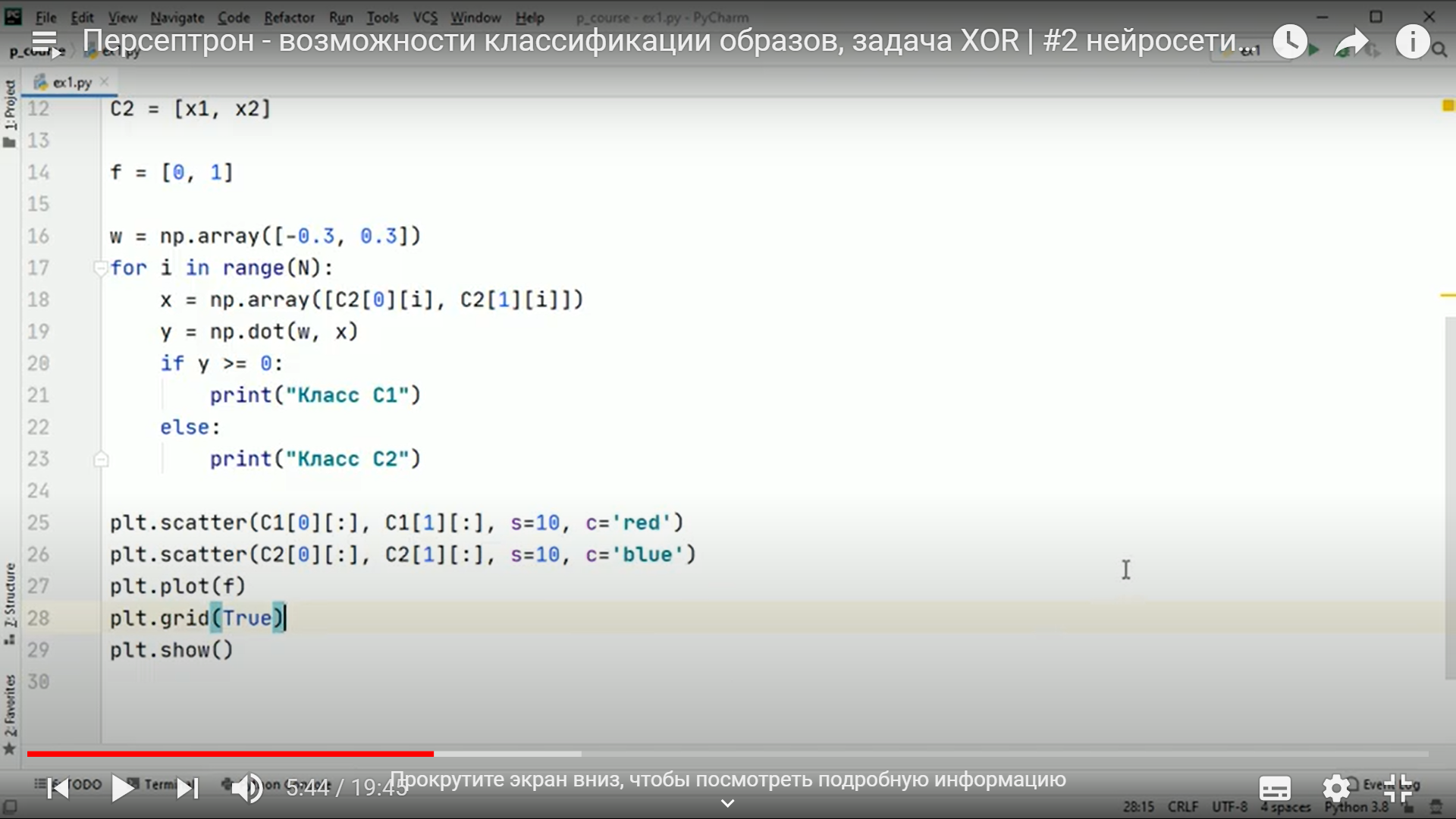  Здесь взят коэффициенты по 0,3 с противоположным знаком. Можно выбрать и любые другие, например, -1 и 1 и т.п. И, как видим, наша НС успешно классифицирует эти образы. Но, если коэффициенты взять не равными, например:  то первый класс будет неверно распознаваться. Это, в частности, означает, что НС неверно настроена на классификацию таких образов и ее весовые коэффициенты нуждаются в корректировке. Вернем все к рабочему состоянию с весами:  И предположим, что все наши образы сдвигаются вверх по оси 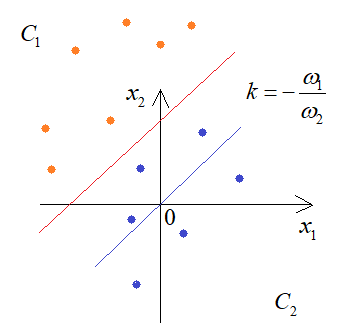 : Теперь, наша разделяющая прямая не сможет верно классифицировать такие образы, т.к. она проходит через начало координат. И как бы мы ее ни крутили, корректного разделения не получится. Необходимо смещение. Поэтому, в НС дополнительно определяют еще один вход для смещения разделяющей гиперплоскости. В английской литературе он называется bias (перевести можно как порог). 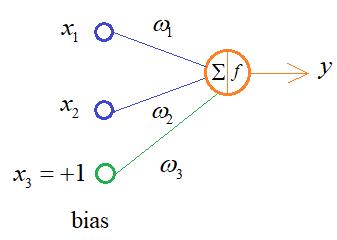 С этим дополнительным входом, наша прямая принимает вид:  то есть, мы можем теперь сдвинуть ее на любое требуемое значение. Давайте предположим, что все образы сдвинуты вверх по оси на величину b. Тогда третий весовой коэффициент НС следует выбрать из уравнения: Определяем все это в нашей программе, добавляем к входному вектору третье значение +1 и теперь наша НС корректно классифицирует такие смещенные образы. 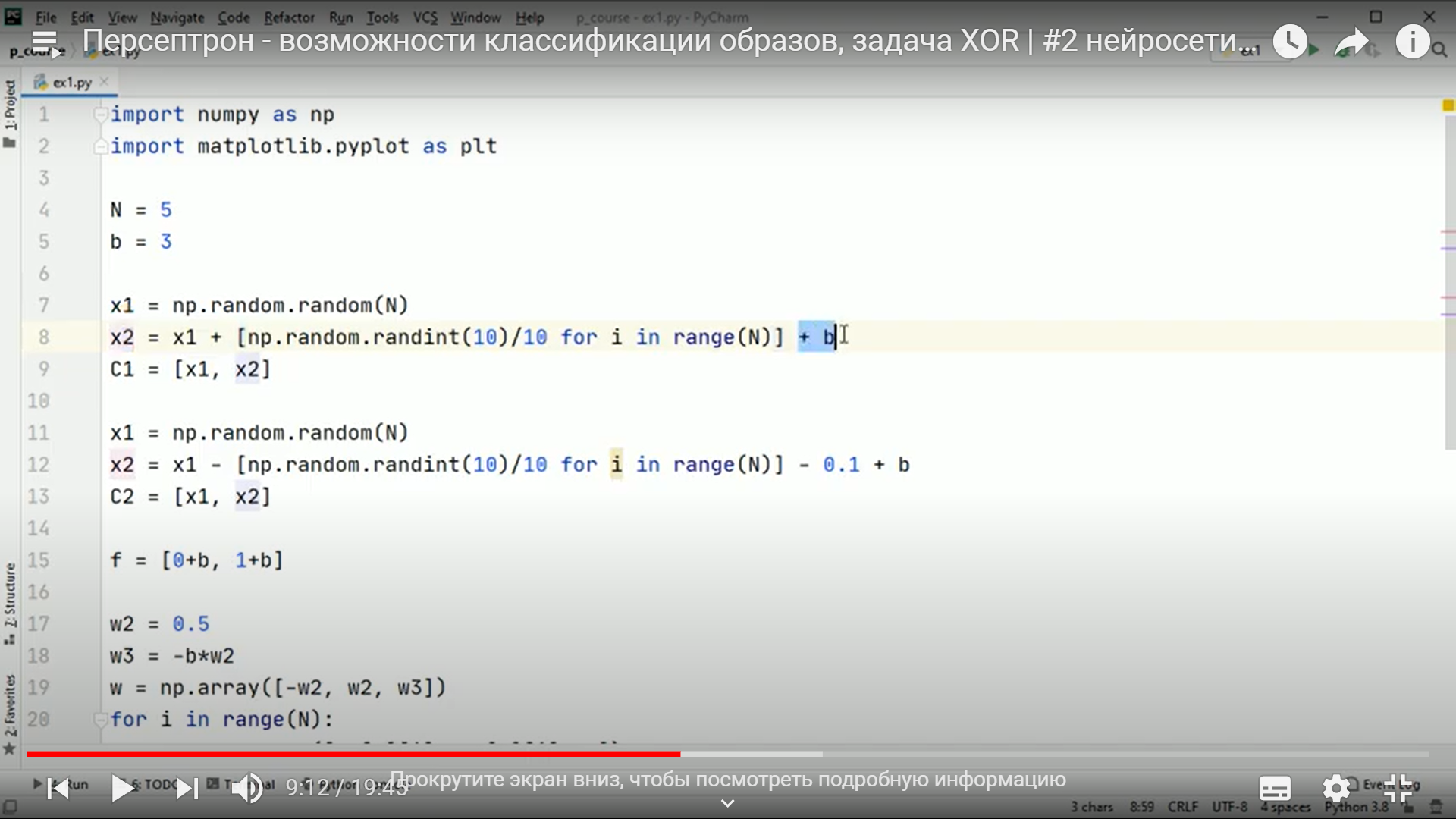 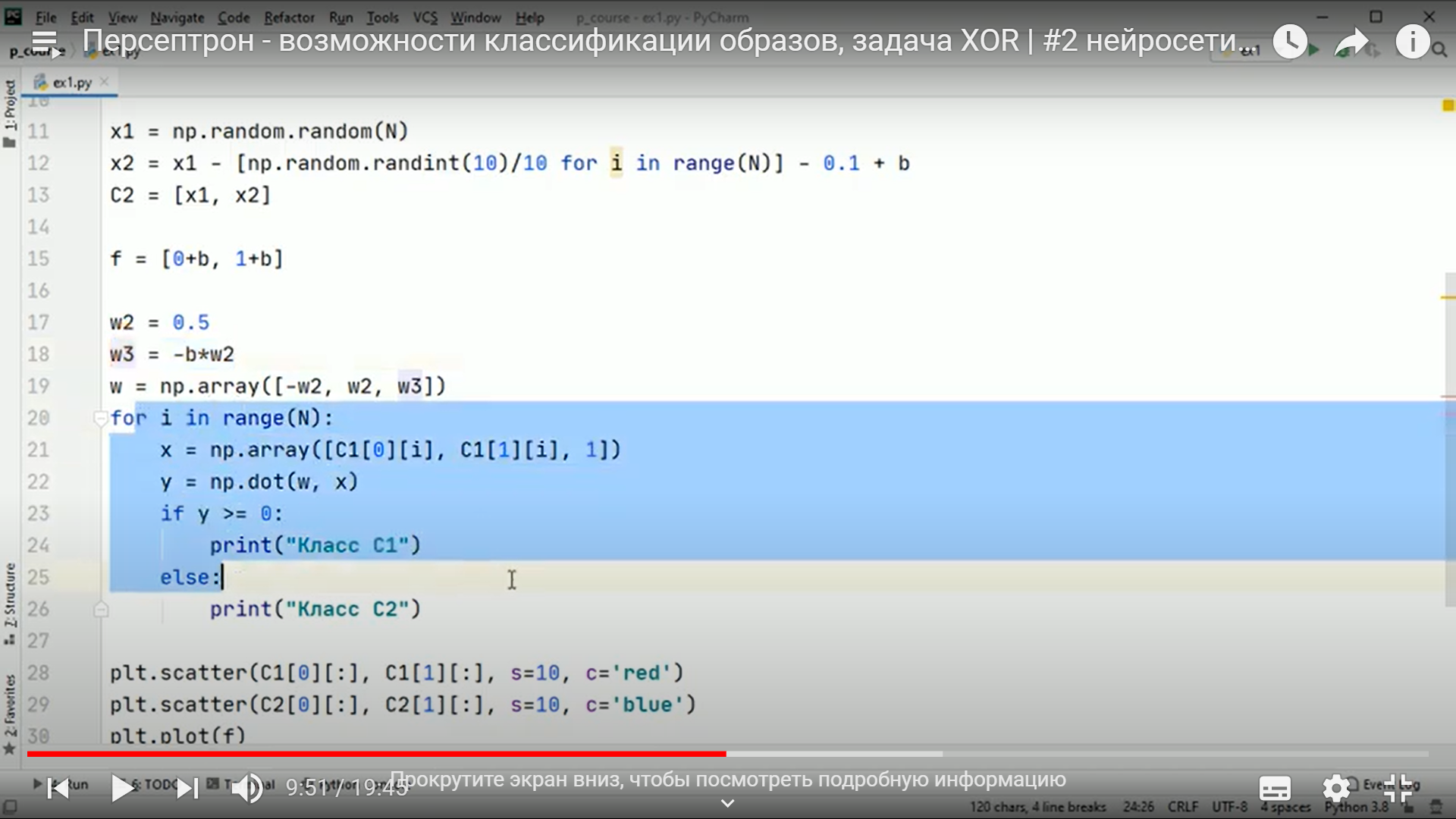 Теперь вы знаете, зачем нужен биас в НС. Это смещение используется во всех современных сетях, а не только в персептроне. Здесь показан пример необходимости его использования. Но та же самая картина сохраняется и для других видов НС с большими размерностями. Задача XOR Рассмотренная нами НС с одним нейроном, может классифицировать только линейно-разделимые образы. Однако, на практике чаще встречаются более сложные задачи. Например, представим, что классы наших образов распределены следующим образом: 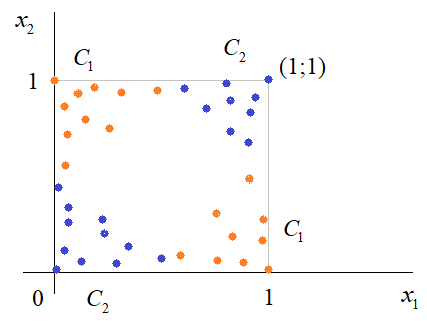 Здесь невозможно провести одну линию для их правильной классификации. Как тогда быть? Например, провести две линии, вот так: 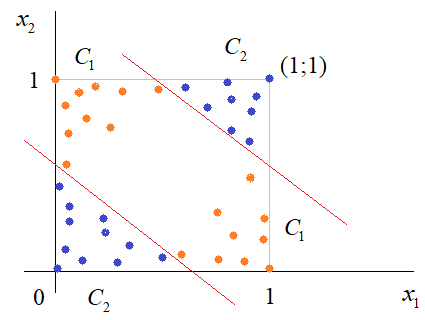 И все, что будет попадать между ними – отнесем к первому классу, а за их пределами – ко второму классу. Что это за НС, которая способна на такие операции? В действительности, все просто: каждая разделительная линия может быть представлена отдельным нейроном, а затем, результат их классификации объединяется результирующим нейроном выходного слоя: 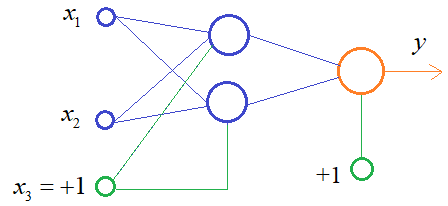 Давайте, для простоты, будем полагать, что на входы подаются только значения 0 или 1:  Тогда, все наши образы будут лежать в углах квадрата: 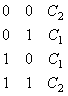 Смотрите, если  , то получаем таблицу истинности для битовой операции XOR (исключающее ИЛИ). Поэтому в литературе задача разделения таких образов получила название задачи XOR.Далее, активационная функция каждого нейрона будет иметь вид:  Осталось определить веса связей НС для решения поставленной задачи классификации. Для начала, положим, что первый нейрон скрытого слоя будет формировать границу:  Учитывая, нашу формулу: Веса входов первого нейрона для можно взять равными: а вес третьей связи:  Все, получили прямую, которая формирует следующее разделение на плоскости: 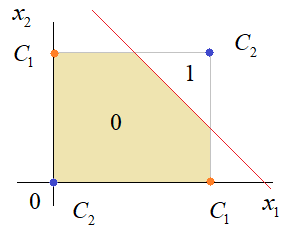 Второй нейрон скрытого слоя будет формировать разделения прямой:  и веса его связей можно взять равными: и  Получаем следующую картину: 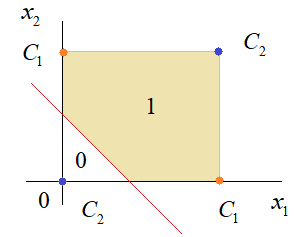 Теперь, нам нужно объединить результаты их работы, чтобы получилась следующая разделяющая область: 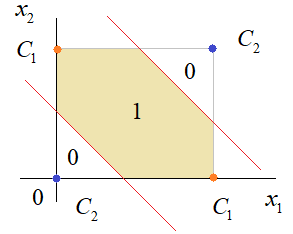 Как это сделать? То есть, как выбрать веса для выходного нейрона, чтобы получить такую картину классификации? Если результаты просто сложить, то получим разделение вида и на выходе активационной функции увидим одну большую область с 1 и одну область с 0. 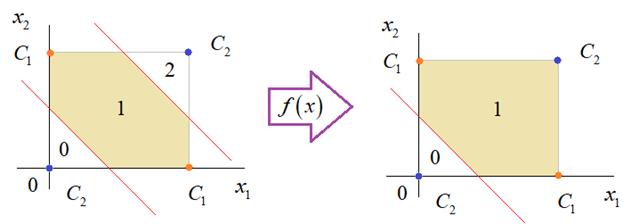 Это не годится. Лучше из второго вычесть первое: 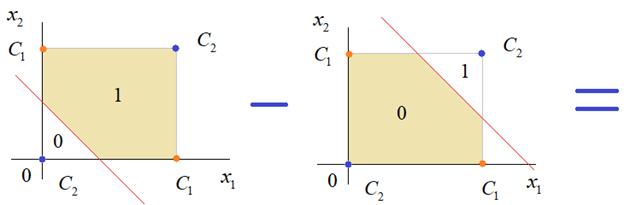 И на входе выходного нейрона будем получать значения: 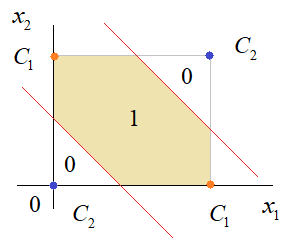 Для надежности сместим эти значения на -0,5 и окончательно получим результат: 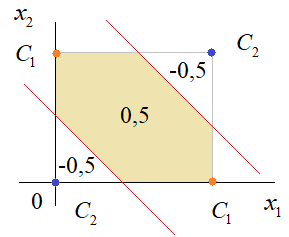 То есть, веса в нашей НС, будут следующими: 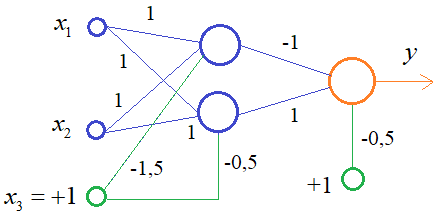 На Python эту НС можно реализовать следующим образом. Как видим, результаты получаются именно такими, какие мы и ожидали, классификация задачи XOR выполнена успешно благодаря добавлению скрытого слоя нейронов. 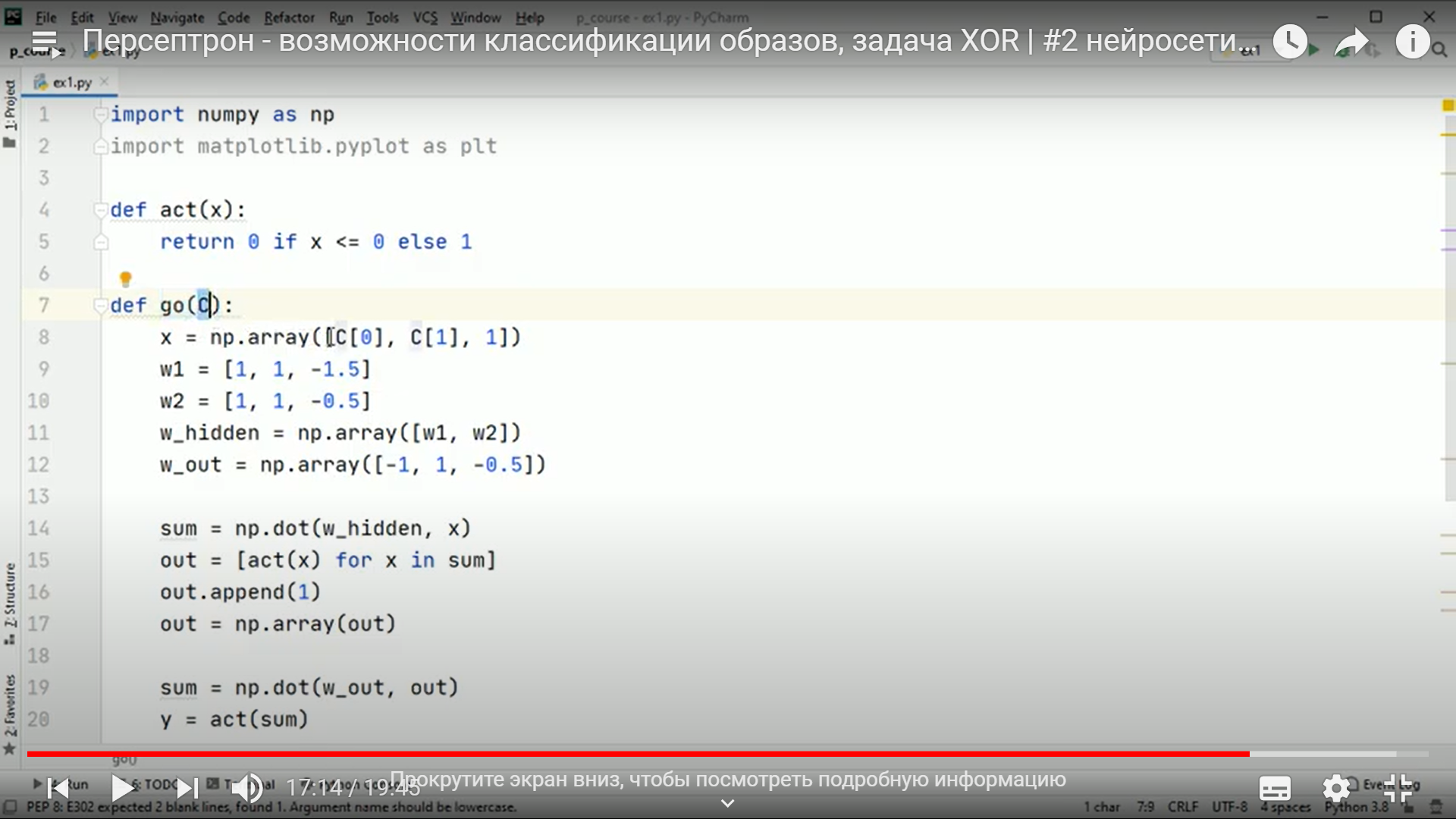 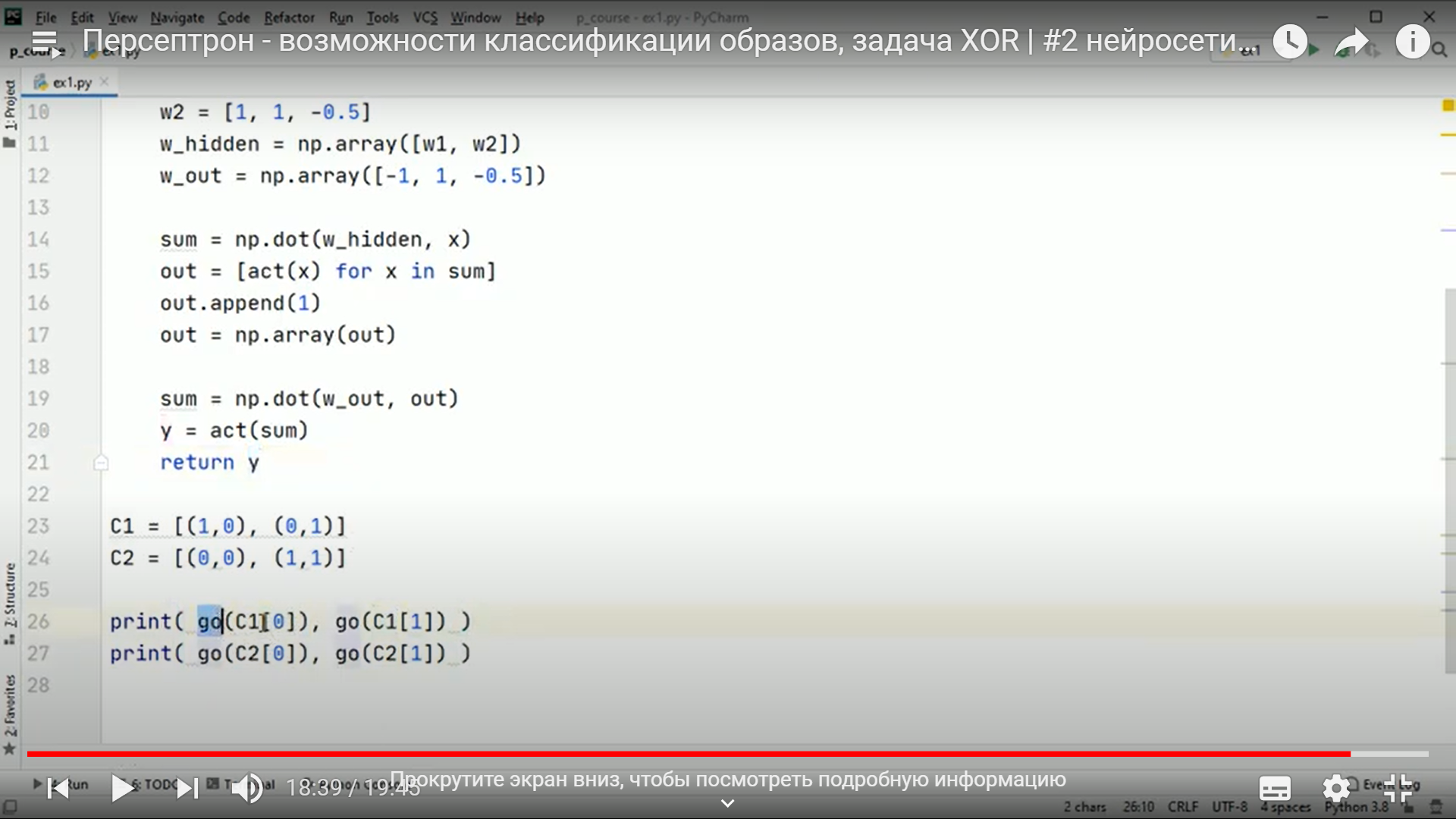 Этот пример хорошо показывает, что добавляя новые нейроны, мы можем получать все более сложные формы разделяющих выпуклых областей, полученные комбинацией разделяющих линий или гиперплоскостей. Это приводит к более сложным схемам классификации, уходящей далеко за пределы линейно-разделимых образов. |