Ответы к 32 Лабораторной работе НГТУ. Первый уровень Дифракция

• Название: Первый уровень Дифракция
• Анкор: Ответы к 32 Лабораторной работе НГТУ
• Дата: 05.11.2022
• Размер: 72.05 Kb.
• Имя файла: lab32_otveti.docx
• Тип: Документы; #771186

Первый уровень:

1. 
   Дифракция – явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием.
   
2. 
   Принцип Гюйгенса-Френеля: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.
   
3. 
   Волновой фронт - это поверхность, до которой дошли колебания к данному моменту времени. Волновой фронт является частным случаем волновой поверхности.
   
4. 
   Волновая поверхность – геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Если источником волны является точка, то волновые поверхности в однородном и изотропном пространстве представляют собой концентрические сферы.
   
5. 
   Отклонение волн от прямолинейного распространения при взаимодействии с препятствием. Из-за дифракции волны огибают препятствия, проникая в область геометрической тени. Возникает при любом (амплитудном или фазовом) локальном нарушении волнового фронта.
   
6. 
   –
   
7. 
   Если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку наблюдения, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или дифракции в параллельных пучках. В противном случае, говорят о дифракции Френеля или дифракции в сходящихся пучках.
   
8. 
   Разделим поверхность волны S на кольцевые зоны, для этого проведем из точки Р сферы радиусом Ро:
   Рa = Рo + λ/2, Рb = Ра + λ/2 = Рo + 2λ/2, Рс = Рb + λ/2 = Рo + 3λ/2
   (О - точка пересечения поверхности волны с линией PQ).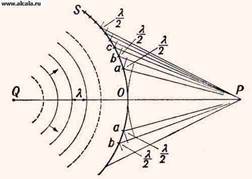
   
   
9. 
   Колеблются в противофазе.
   

10) В противофазе гасят друг друга.

11) –

12/13) Если на пути световых волн поставить экран с отверстием, в котором укладывается четное число зон Френеля, то в точке P будет минимум – ослабление света:


Если в отверстии укладывается нечетное число зон Френеля, то в точке P будет максимум – усиление света:



14/15) Если число зон Френеля четное, то в точке P наблюдается дифракционный минимум.
Если число зон Френеля нечетное, то наблюдается дифракционный максимум.

16) От ширины щели.

17) –

18) –

19) –

Уровень 2

Задание 1.

А) Амплитуда, создаваемая в некоторой точке Р всей сферической волновой поверхностью, равна половине амплитуды первой зоны. Следовательно, распространение света от S к Р происходит так, будто световой поток распространяется внутри очень узкого канала вдоль линии SР. т. е. прямолинейно.

Б) Дифракция на круглом отверстии.
Рис. 4
Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути
экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В,
лежащей на линии, соединяющей S с центром отверстия (рис. 4). Экран параллелен плоскости
отверстия и находится от него на расстоянии b.
Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной
картины зависит от числа зон Френеля, открываемых отверстием.
Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами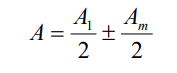

где знак плюс соответствует нечетным m
и минус — четным т.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке
В будет больше, чем при свободном распространении волны.
Если четное, то амплитуда (интенсивность) будет равна нулю.
Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А1, т. е. вдвое больше,
чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше

Задание 2.

В приведённом ниже расчёте по-прежнему пользуемся принципом Гюйгенса-Френеля. Рассмотрим плоскую монохроматическую волну, падающую на узкую прямоугольную щель. Пусть уравнение волны даётся соотношением:

, (3)

где  – амплитуда волны, – волновое число, – расстояние, которое волна прошла от фронтаAB. Вклад элементарного участка волновой поверхности шириной  , отстоящего на расстояниих от точки А (см. рис. 1) даётся соотношением:

.(5)

Проинтегрировав это выражение по всей ширине щели b, найдем амплитуду результирующей волны в соответствующей точке экрана М_φ. Запишем выражение для амплитуды волны E_0 в точке М_φ: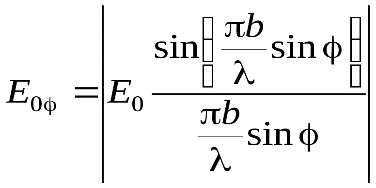

. (6)

Вводя обозначение

,(7)

получим

.(8)

При u  0 sin u  u, lim(sin u/u) = 1, поэтому при  = 0 дробь в выражении (6) превращается в единицу. Отсюда следует, что E₀ есть амплитуда в точке М₀ (против центра линзы).

Интенсивность света пропорциональна квадрату амплитуды. Следовательно,

. (9)

Из формул (6,9) следует, что если

bsin =  k (k = 1,2,3, …),

то интенсивность обращается в нуль (наблюдаются минимумы порядков

k =1, k = 2, и т.д.) Это согласуется с формулой (1).

• 
  Задание 3. Условие для главных максимумов дифракционной картины от дифракционной решетки 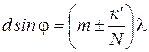  , где   Между соседними главными максимумами лежат прежний минимум и  добавочный минимум, где N– число щелей в решетке. Эти минимумы возникают в тех направлениях, для которых колебания от всех щелей взаимно гасят друг друга, т.к. сложение амплитуд колебаний от отдельных щелей векторное. Условия прежнего минимума   . Условия для добавочных минимумов имеет вид:  , где   . Положение главных максимумов зависит от длины волны  . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный расположен дальше от центра, чем фиолетовый. Центральный максимум будет белого цвета.
  

Задание 4 Положение дифракционных максимумов и минимумов от одной щели не зависит от её положения, а определяется направлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракционной картины. Следовательно, картины, создаваемые каждой щелью в отдельности будут совершенно одинаковыми.

Результирующую картину можно определить путем сложения этих двух дифракционных картин с учётом интерференции когерентных волн, идущих от каждой из щелей в соответствии с принципом Гюйгенса-Френеля. Очевидно, что в тех направлениях, в которых ни одна из щелей света не дает света, не будет света и при двух параллельных щелях. Условие минимума интенсивности (10.8) , где = ±1, 2, 3, ..., выполняется и в данном случае. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются и возникают добавочные минимумы.